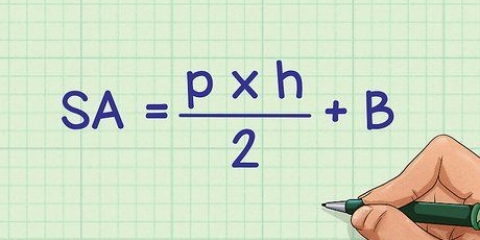Per le forme piccole si possono usare i centimetri, mentre per le circonferenze più grandi sono più indicati metri o chilometri. Quando i lati opposti dei rettangoli sono uguali, devi solo misurare uno dei lati opposti. 
Continua con l`esempio: immagina che oltre a una lunghezza di 3 cm, la larghezza del tuo rettangolo sia di 5 cm. 

Quindi in questo esempio calcoli 3 + 3 + 5 + 5 = 16 (il perimetro). Puoi anche usare la formula 2 x (lunghezza + larghezza) per i rettangoli, poiché la lunghezza e la larghezza dei lati opposti sono uguali e quindi raddoppiate. Quindi nel nostro esempio questo è: 2 x 8 = 16. 
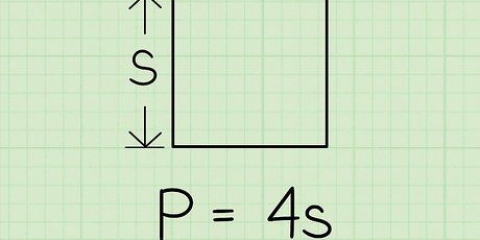
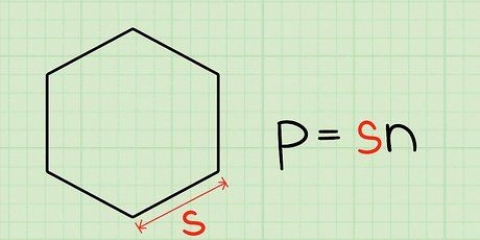
Quadrato: lunghezza di ogni lato x 4 Triangolo: somma tutti i lati insieme Poligono irregolare: somma tutti i lati insieme Cerchio: 2 x π x raggio o π x diametro. Il simbolo π sta per Pi (torta pronunciata). Se hai un tasto π sulla calcolatrice, puoi usarlo per essere più preciso quando usi questa formula. In caso contrario, puoi arrotondare il valore di π a 3,14. Il termine `raggio` si riferisce alla distanza tra il centro di un cerchio e il suo confine esterno (circonferenza), mentre `diametro` si riferisce alla lunghezza di una linea immaginaria tra due punti opposti sulla circonferenza di un cerchio passante per il centro di il cerchio... il cerchio va. 

Puoi dividere la forma in segmenti verticali e orizzontali di un`unità (cm, m) se vuoi visualizzare come apparirà la misurazione dell`area. 
Puoi scrivere `unità quadrate/unità quadrate` come: cmq m² km² 
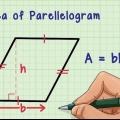
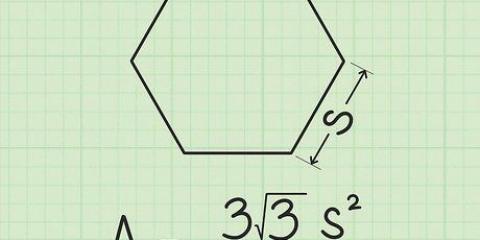
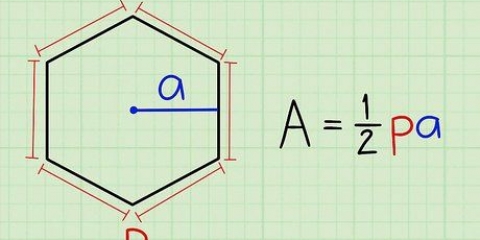
Parallelogramma: base x altezza Quadrato: lato 1 x lato 2 Triangolo: ½ x base x altezza. Alcuni matematici usano la notazione: A=½bh. Cerchio: π x r² (dove r = raggio) Il termine "raggio" si riferisce alla distanza tra il centro di un cerchio e il suo confine esterno (circonferenza), e i due piccoli in apice (il quadrato) indica che il valore a cui appartengono i due è moltiplicato per se stesso.
Determina area e perimetro
Contenuto
Il perimetro è la lunghezza dell`intero confine esterno di una figura piana (bidimensionale) e l`area è la misura della sua dimensione. L`area e il perimetro sono misurazioni estremamente utili che possono essere utilizzate in progetti domestici, costruzioni, progetti fai-da-te e per stimare la quantità di materiali di cui potresti aver bisogno. Ad esempio, se vuoi dipingere una stanza, dovrai sapere quanta vernice ti serve o, in altre parole, quanto superficie la vernice può coprire. Lo stesso si può dire quando si organizza un giardino, si costruisce una recinzione o si fanno altre faccende domestiche. In queste situazioni, è possibile utilizzare l`area e il perimetro per risparmiare tempo e denaro nell`acquisto dei materiali.
Passi
Parte 1 di 2: Determinazione della circonferenza

1. Determina la forma che vuoi misurare. Il perimetro è il confine esterno attorno a una figura geometrica chiusa e forme diverse richiedono approcci diversi. Se la forma di cui si desidera trovare il perimetro non è una forma chiusa, non è possibile determinare il perimetro.
- Se è la prima volta che calcoli il perimetro, prova un rettangolo o un quadrato. Queste forme regolari facilitano la determinazione del perimetro.

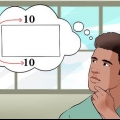
2. Disegna un rettangolo su un pezzo di carta. Usi questo rettangolo come forma pratica e ne determini il perimetro. Assicurati che i lati opposti del tuo rettangolo abbiano la stessa lunghezza.

3. Determina la lunghezza di un lato del tuo rettangolo. Puoi farlo con un righello, un metro a nastro o inventando il tuo esempio. Scrivi questo numero accanto al lato che rappresenta, in modo da non dimenticare la lunghezza. Supponiamo che la lunghezza di un lato del tuo rettangolo sia 3 cm.

4. Determina la larghezza di un lato del tuo rettangolo. Puoi misurare la larghezza con un righello, un metro a nastro o facendo il tuo esempio. Scrivi il valore per la tua larghezza accanto al lato orizzontale del rettangolo che rappresenta.

5. Scrivi le misure corrette sui lati opposti del tuo rettangolo. I rettangoli hanno quattro lati, ma la lunghezza dei lati opposti sarà la stessa. Questo vale anche per la larghezza del tuo rettangolo. Scrivi la lunghezza e la larghezza utilizzate nell`esempio (rispettivamente 3 e 5 cm) sui lati opposti del rettangolo.

6. Aggiungi tutti i lati insieme. Sotto l`esempio che hai fatto o annotato, scrivi quanto segue: lunghezza + lunghezza + larghezza + larghezza.

7. Regola il tuo approccio per forme diverse. Sfortunatamente, forme diverse richiedono formule diverse per il perimetro. Negli esempi del mondo reale, puoi misurare il confine esterno di qualsiasi forma geometrica chiusa per determinarne il perimetro. Ma puoi anche usare le seguenti formule per trovare il perimetro di altre forme comuni:
Parte 2 di 2: Determinazione dell`area

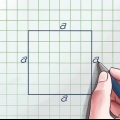
1. Determina le dimensioni della tua forma. Disegna un rettangolo o usa lo stesso rettangolo che hai disegnato per determinare il perimetro. In questo esempio, stai calcolando l`area di un rettangolo, usando la sua altezza e larghezza.
- Puoi lavorare con un righello o un metro a nastro o inventare il tuo esempio. In questo esempio, la lunghezza e la larghezza sono uguali all`esempio precedente utilizzato per trovare il perimetro: rispettivamente 3 e 5 .

2. Comprendere il vero significato della superficie. Determinare l`area all`interno di un perimetro è come dividere lo spazio vuoto all`interno della propria forma in 1 per 1. quadrati. L`area può essere più piccola o più grande del perimetro, a seconda della forma.

3. Moltiplica la lunghezza del tuo rettangolo per la larghezza. Nell`esempio: area = 3 x 5, ovvero 15 metri quadrati. L`unità di misura dell`area deve essere sempre scritta in unità quadrate (km quadrati, metri quadrati, ecc.).

4. Cambia la tua formula a seconda della forma. Sfortunatamente, forme geometriche diverse richiederanno un approccio diverso per calcolare l`area. È possibile utilizzare le seguenti formule per trovare l`area di alcune forme comuni:
Consigli
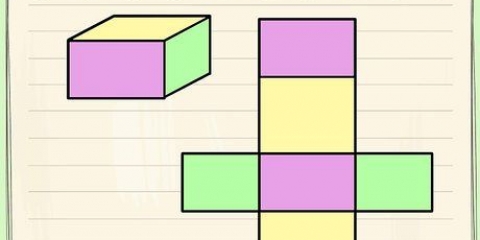
- Queste formule di area e perimetro funzionano solo per l`area (il volume) di una forma piatta. Se devi trovare il contenuto di una forma tridimensionale (il volume), devi cercare formule per il volume, come quelle per coni, cubi, cilindri, prismi e piramidi.
Necessità
- Carta
- Matita
- Calcolatrice (opzionale)
- Metro a nastro (opzionale)
- Righello (opzionale)
Articoli sull'argomento "Determina area e perimetro"
Condividi sui social network:
Popolare