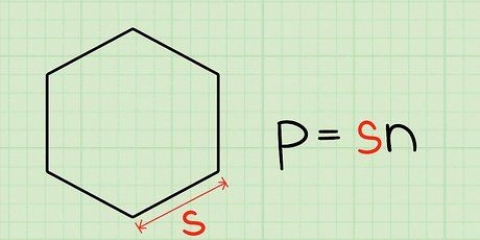
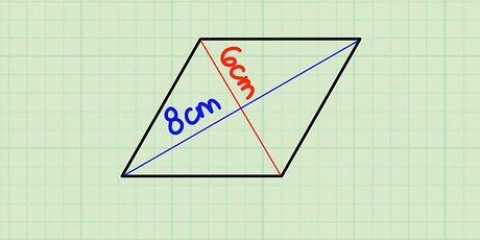
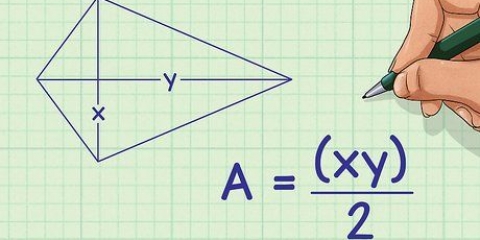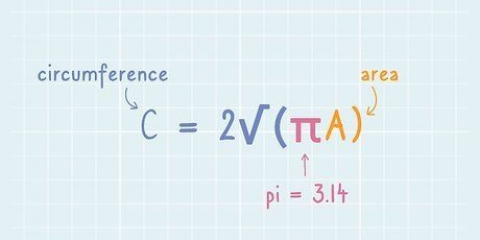Se conosci la circonferenza, dividila per 6 per calcolare la lunghezza di un lato. Ad esempio: la lunghezza della circonferenza è di 54 cm; dividi questo per 6 e ottieni 9 cm come risposta per la lunghezza del lato.
Se conosci solo l`apotema, puoi trovare la lunghezza di un lato inserendo il valore dell`apotema nella formula a = x√3 e moltiplica la risposta per 2. Questo perché l`apotema forma il lato di un triangolo 30-60-90. Ad esempio, se l`apotema è 10√3, allora x è uguale a 10 e la lunghezza di un lato è 10 x 2 = 20. 

(3√3 x 9)/2 = (3√3 x 81)/2 = (243√3)/2 = 420.8/2 = 210.4 cm 


L`apotema è il lato x√3. Ecco perché puoi inserire questo valore nella formula a = x√3. Ad esempio, se la lunghezza dell`apotema è 5√3, secondo la formula: 5√3 cm = x√3 o x = 5 cm. Risolvendo x hai trovato la lunghezza del lato corto del triangolo, x = 5. Dato che è la metà della lunghezza di un lato dell`esagono, puoi moltiplicarlo per 2 per ottenere l`intera lunghezza del lato. 5 cm x 2 = 10 cm. Ora che sai che la lunghezza totale di un lato è uguale a 10, tutto ciò che devi fare è moltiplicarlo per 6 per ottenere il perimetro dell`esagono. 10 cm x 6 = 60 cm 
Area = 1/2 x perimetro x apotema Area = 1/2 x 60 cm x 5√3 cm 
1/2 x 60 cm x 5√ 3 cm = 30 x 5√3 cm = 150√3 cm = 259. 8 cm 

4 x 7 = 28 9 x 2 = 18 11 x 2 = 22 2 x 5 = 10 1 x 7 = 7 4 x 10 = 40 28 + 18 + 22 + 10 + 7 + 40 = 125 
10 x 9 = 90 7 x 11 = 77 2 x 2 = 4 2 x 1 = 2 5 x 4 = 20 7 x 4 = 28 90 + 77 + 4 + 2 + 20 + 28 = 221 




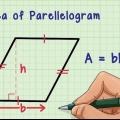
Un certo tipo di esagono irregolare è costituito da due parallelogrammi. Per calcolare le aree di questi, moltiplica la base per l`altezza, proprio come un rettangolo, quindi somma le loro aree.
Calcola l'area di un esagono
Contenuto
Un esagono o esagono è un poligono con sei lati e angoli. Un esagono regolare ha sei lati e angoli uguali ed è composto da sei triangoli equilateri. Esistono diversi modi per calcolare l`area di un esagono irregolare o regolare. Se vuoi sapere come, segui questi passaggi.
Passi
Metodo 1 di 4: L`area di un esagono regolare con un dato lato

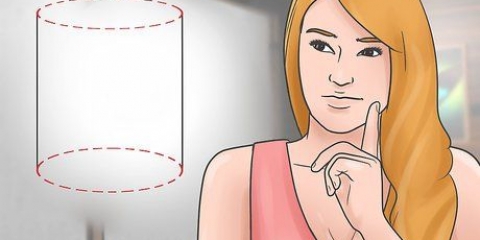
1. Annota la formula per calcolare l`area di un esagono se conosci la lunghezza di un lato. Poiché un esagono regolare è costituito da sei triangoli equilateri, la formula per trovare l`area di un esagono è derivata dalla formula per calcolare l`area di un triangolo equilatero. La formula per questo è: Area = (3√3 s)/ 2 dove`s` è la lunghezza di un lato dell`esagono regolare.

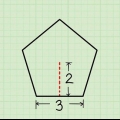
2. Determina la lunghezza del lato. Se sai già qual è la lunghezza, scrivila. In questo caso, la lunghezza di un lato è di 9 cm. Se non conosci la lunghezza ma sai quanto è lungo il perimetro, o conosci il deapotema (la lunghezza della linea dal centro dell`esagono che è perpendicolare a un lato), puoi comunque ottenere la lunghezza del lato di un esagono calcolato. Ecco come farlo:

3. Immettere la lunghezza del lato nella formula. Poiché sai che la lunghezza di un lato del triangolo è 9, puoi semplicemente inserirlo nella formula originale. Si presenta così: Area = (3√3 x 9)/2

4. Semplifica la tua risposta. Trova il valore dell`equazione e scrivi la tua risposta. Ricorda, dal momento che stai calcolando l`area, la risposta dovrebbe essere in metri quadrati. Qui puoi leggere come farlo
Metodo 2 di 4: L`area di un esagono regolare con un apotema noto

1. Annota la formula per calcolare l`area di un esagono con un dato apotema. La formula è semplice: Area = 1/2 * perimetro* apotema.

2. Nota l`apotema. Supponiamo che l`apotema sia 5√3 cm.

3. Usa l`apotema per trovare il perimetro. Poiché l`apotema è perpendicolare al lato dell`esagono, forma un lato di un triangolo 30-60-90. I lati di un triangolo 30-60-90 hanno il rapporto: xx√3-2x, dove x è la lunghezza del lato più corto (opposto all`angolo di 30 gradi), x√3 è la lunghezza del lato lungo (opposto l`angolo di 60 gradi) e 2x l`ipotenusa.

4. Inserisci tutti i valori noti nella formula. Calcolare la circonferenza è stata la parte più difficile. Ora non ti resta che risolvere l`apotema e il perimetro usando la formula:

5. Semplifica la tua risposta. Semplifica l`espressione finché non hai rimosso tutte le radici quadrate dall`equazione. Assicurati che la tua risposta finale sia in metri quadrati.
Metodo 3 di 4: calcola l`area di un esagono irregolare con i vertici dati

1. Elenca le coordinate xey di tutti i vertici. Se conosci i vertici dell`esagono, la prima cosa che fai è creare una tabella con due colonne e sette righe. Ogni riga prende il nome dai sei punti (Punto A, Punto B, Punto C, ecc.) e ogni colonna prende il nome dalle coordinate x o y di quei punti. Elenca le coordinate xey dal punto A al punto F. Ripetere le coordinate del punto A alla fine dell`elenco. Prendiamo il seguente esempio, con il formato Nome:(x,y):
- R: (4, 10)
- B: (9, 7)
- C: (11, 2)
- D: (2, 2)
- E: (1, 5)
- F: (4, 7)
- A (di nuovo): (4, 10)

2. Moltiplica la coordinata x di ciascun punto per la coordinata y del punto successivo. Posiziona i risultati a destra della tabella. Quindi somma i risultati insieme.

3. Moltiplica la coordinata y di ogni punto per la coordinata x del punto successivo. Somma i risultati insieme.

4. Sottrarre la seconda somma dalla prima somma. Sottrarre 221 da 125. 125 - 221 = -96. Ora prendi il valore assoluto di questa risposta: 96. L`area non può che essere positiva.

5. Dividi per due la differenza calcolata. Dividendo 96 per 2 si ottiene l`area dell`esagono irregolare. 96/2 = 48. Ricorda che l`unità della tua risposta è il metro quadrato. La risposta alla domanda è quindi 48 m.
Metodo 4 di 4: Altri metodi per calcolare l`area di un esagono

1. Trovare l`area di un esagono in cui un vertice è sconosciuto. Se sai di avere a che fare con un esagono regolare con triangoli mancanti, la prima cosa che fai è calcolare l`area, come se l`esagono fosse completo. Quindi calcola semplicemente l`area dei triangoli formati dai vertici e sottraila dall`area totale. Questo restituisce l`area dell`esagono irregolare.
- Un esempio: se hai calcolato che l`area dell`esagono regolare è 60 cm e sai che l`area dei triangoli mancanti è 10 cm, allora l`area dell`esagono irregolare è: 60 cm - 10 cm = 50 cm.
- Se sai che all`esagono manca esattamente un triangolo, è anche possibile trovare l`area dell`esagono irregolare moltiplicando l`area dell`esagono regolare o l`area totale per 5/6, perché l`esagono irregolare occupa un`area che esiste da 5 dei 6 triangoli dell`esagono regolare. Se ne mancano due, moltiplicare per 4/6 e così via.

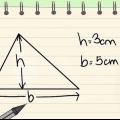
2. Rompi un esagono irregolare in altri triangoli. Può darsi che l`esagono irregolare sia formato da quattro triangoli di forma disuguale. Per trovare l`intera area di questo esagono devi trovare l`area di ogni singolo triangolo e poi sommarli. Esistono diversi modi per trovare l`area di un triangolo, a seconda di ciò che sai.

3. Cerca altre forme nell`esagono irregolare. Se non riesci a trovare i triangoli, controlla se riesci a trovare altre forme, magari un quadrato o un rettangolo. Una volta scoperte le altre forme, somma le aree per calcolare quella dell`intero esagono.
Articoli sull'argomento "Calcola l'area di un esagono"
Condividi sui social network:
Popolare