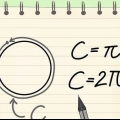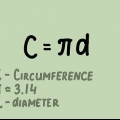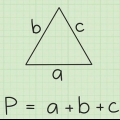Come Calcolare il Raggio di un Cerchio

Contenuto

Passi

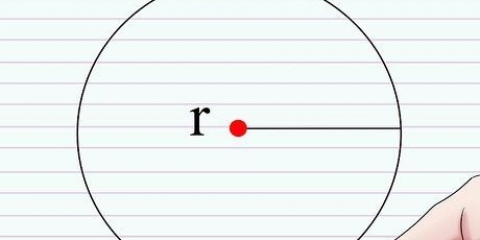
Il raggio di un cerchio è la distanza dal centro del cerchio al bordo. Il diametro di un cerchio è la lunghezza della retta che può essere tracciata tra due punti sulla sfera o cerchio e attraverso il suo centro.Spesso ti viene chiesto di calcolare il raggio di un cerchio in base ad altri dati. In questo articolo imparerai come calcolare il raggio di un cerchio in base a un dato diametro, circonferenza e area. Il quarto metodo è un metodo più avanzato per determinare il centro e il raggio di un cerchio in base alle coordinate di tre punti sul cerchio.

Passi

Metodo 1 di 3: calcola il raggio se conosci il diametro

Immagine titolata Calcola il raggio di un cerchio Passaggio 1

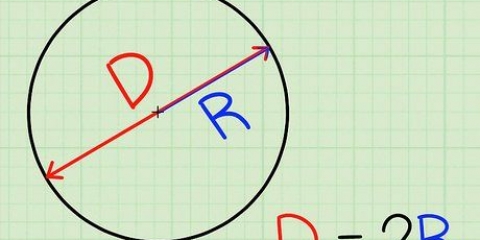
1. Ricorda qual è il diametro. Il diametro di un cerchio è la lunghezza della retta che può essere tracciata tra due punti sulla sfera o cerchio e attraverso il suo centro. Il diametro è la linea più lunga che può essere tracciata attraverso un cerchio e divide il cerchio in due metà. La lunghezza del diametro è anche uguale alla lunghezza del doppio del raggio. La formula per il diametro è la seguente: D= 2r, dove "D" sta per diametro e "R" per trave. La formula per il raggio può essere ricavata dalla formula precedente ed è quindi: r = D/2.

Immagine titolata Calculate the Radius of a Circle Step 2

2. Dividi il diametro per 2 per trovare il raggio. Se conosci il diametro di un cerchio tutto ciò che devi fare è dividerlo per 2 per trovare il raggio.

Ad esempio, se il diametro di un cerchio è 4, la retta è 4/2 o 2.

Metodo 2 di 3: calcola il raggio se conosci la circonferenza

Immagine titolata Calcola il raggio di un cerchio Passaggio 3

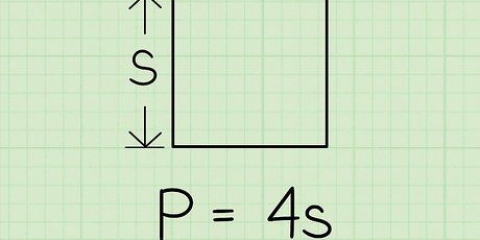
1. Ricordi la formula per la circonferenza di un cerchio?. La circonferenza di un cerchio è la distanza attorno al cerchio. Un altro modo per vederlo è questo: il perimetro è la lunghezza della linea che ottieni se tagli il cerchio aperto in un punto e stendi la linea dritta. La formula per la circonferenza di un cerchio è O = 2πr, dove "R" è il raggio e π è la costante pi, ovvero 3,14159... La formula per il raggio è quindi r = O/2π.

Di solito puoi arrotondare pi greco a due cifre dopo la virgola (3,14), ma prima verifica con il tuo insegnante.

Immagine titolata Calcola il raggio di un cerchio Passaggio 4

2. Calcola il raggio con la circonferenza data. Per calcolare il raggio in base alla circonferenza, dividere la circonferenza per 2π, o 6,28

Ad esempio, se la circonferenza è 15, il raggio è r = 15/2π, ovvero 2,39.

Metodo 3 di 3: calcola il raggio se conosci le coordinate di tre punti sul cerchio

Immagine titolata Calculate the Radius of a Circle Step 9

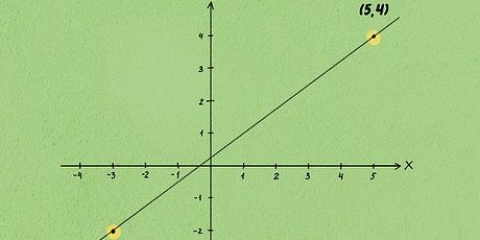
1. Comprendi che tre punti possono definire un cerchio. Tre punti qualsiasi su una griglia definiscono un cerchio tangente ai tre punti. È il cerchio circoscritto del triangolo che forma i punti. Il centro del cerchio può cadere all`interno o all`esterno del triangolo, a seconda della posizione dei tre punti, e allo stesso tempo è il "intersezione" del triangolo.È possibile calcolare il raggio del cerchio se si conoscono le coordinate xy dei tre punti in questione.

Ad esempio, prendiamo tre punti definiti come segue: P1 = (3,4), P2 = (6, 8) e P3 = (-1, 2).

Immagine titolata Calculate the Radius of a Circle Step 10

2. Usa la formula della distanza per calcolare le lunghezze dei tre lati del triangolo, che chiamiamo a, b e c. La formula per la distanza tra due coordinate (x₁, y₁) e (x₂, y₂) è il seguente: distanza = √(( x₂ - X₁) + (s₂ - y₁)). Ora elabora le coordinate dei tre punti in questa formula per trovare le lunghezze dei tre lati del triangolo.

Immagine titolata Calculate the Radius of a Circle Step 11

3. Calcola la lunghezza del primo lato a, che va dal punto P1 al punto P2. Nel nostro esempio, le coordinate di P1 (3.4) e di P2 (6.8), quindi la lunghezza del lato a = √((6 - 3) + (8 - 4)).

a = √(3 + 4)

a = √(9 + 16)

a = √25

a = 5

Immagine titolata Calculate the Radius of a Circle Step 12

4. Ripetere la procedura per trovare la lunghezza del secondo lato b, che va da P2 a P3. Nel nostro esempio, le coordinate di P2 (6.8) e di P3 sono (-1.2), quindi la lunghezza del lato b = √((-1 - 6) + (2 - 8)).

b= √(-7 + -6)

b = √(49 + 36)

b = √85

b = 9.23

Immagine titolata Calculate the Radius of a Circle Step 13

5. Ripetere il processo per trovare la lunghezza del terzo lato c, che va da P3 a P1. Nel nostro esempio, le coordinate di P3 (-1,2) e di P1 (3,4), quindi la lunghezza del lato c =√((3 - -1) + (4 - 2)).

c= √(4 + 2)

c = √(16 + 4)

c = √20

c = 4.47

Immagine titolata Calcola il raggio di un cerchio Passaggio 14

6. Usa queste lunghezze nella formula di ricerca del raggio: (abc)/(√(a + b + c)(b + c - a)(c + a - b)(a + b - c)).. Il risultato è il raggio del nostro cerchio!

Le lunghezze del triangolo sono le seguenti: a = 5, b = 9.23 e c = 4.47. Quindi la formula per il raggio si presenta così: r = (5 * 9.23*4.47)/(√(5 + 4.47+9.23)(4.47+9.23 - 5)(9.23 + 5 - 4.47)(5 + 4.47 – 9.23)).