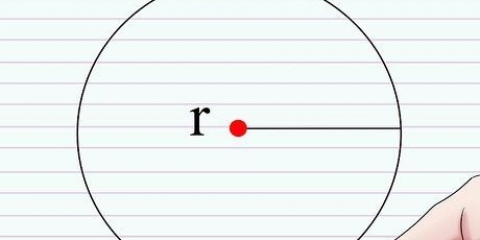
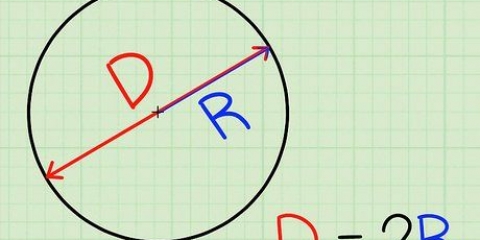
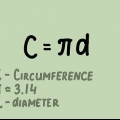Il raggio (R) di un cerchio è la distanza da un punto del cerchio al centro del cerchio. Il diametro (D) di una circonferenza è la distanza da un punto della circonferenza ad un altro punto direttamente opposto alla circonferenza, passante per il centro della circonferenza. La lettera greca pi (π) sta per il rapporto tra la circonferenza divisa per il diametro ed è rappresentata dal numero 3.14159265..., un numero irrazionale che non ha né una cifra finale né uno schema riconoscibile di cifre ripetute. Questo numero viene spesso arrotondato a 3,14 per i calcoli standard. 
Nella maggior parte dei problemi di matematica viene fornito il raggio o il diametro. 
Ad esempio: qual è la circonferenza di un cerchio con un raggio di 3 cm? Scrivi la formula: C = 2πr Completa le variabili: C = 2π3 Moltiplicare: C = (2*3*π) = 6π = 18,84 cm Ad esempio: qual è la circonferenza di un cerchio con un diametro di 9 m? Scrivi la formula: C = πd Completa le variabili: C = 9π Moltiplicare: C = (9*π) = 28,26 m 
Determina la circonferenza di un cerchio con un diametro di 5 m. C = πd = 5π = 15,7 m Determina la circonferenza di una circonferenza di raggio 10 m. C = 2πr = C = 2π10 = 2 *10 *π = 62,8 m. 

Il raggio (R) di un cerchio è la distanza da un punto del cerchio al centro del cerchio. Il diametro (D) di una circonferenza è la distanza da un punto della circonferenza ad un altro punto direttamente opposto alla circonferenza, passante per il centro della circonferenza. La lettera greca pi (π) sta per il rapporto tra la circonferenza divisa per il diametro ed è rappresentata dal numero 3.14159265..., un numero irrazionale che non ha né una cifra finale né uno schema riconoscibile di cifre ripetute. Questo numero viene solitamente arrotondato a 3,14 per i calcoli di base. 
Nella maggior parte dei problemi di matematica viene fornito il raggio o il diametro. 
Ad esempio: qual è l`area di un cerchio con un raggio di 3 m? Scrivi la formula: A = R. Compila le variabili: A = π3. Al quadrato il raggio: R = 3 = 9 Moltiplica per pi: un = 9π = 28,26 m Ad esempio: qual è l`area di un cerchio con un diametro di 4 m? Scrivi la formula: A = π(d/2). Compila le variabili: A = π(4/2). Dividi il diametro per 2: d/2 = 4/2 = 2 Al quadrato il risultato: 2 = 4 Moltiplica per pi: un = 4π = 12,56 m 
Trova l`area di un cerchio con un diametro di 7 m. A = π(d/2) = π(7/2) = π(3,5) = 12,25 * π= 38,47 m. Trova l`area di un cerchio con un raggio di 3 m. A = πr = π * 3 = 9 * π = 28,26 m 

Ad esempio: calcola la circonferenza di un cerchio con raggio (x + 1). Scrivi la formula: C = 2πr Inserisci le informazioni fornite: C = 2π(x+1) 
Ad esempio: calcola la circonferenza di una circonferenza di raggio (x = 1). C = 2πr = 2π(x+1) = 2πx + 2π1 = 2πx +2π = 6,28x + 6,28 Se il valore di `x` viene fornito più avanti nel problema, puoi collegarlo e ottenere un numero intero. 
Trova l`area di un cerchio con raggio 2x. A = πr = π(2x) = π4x = 12,56x Trova l`area di un cerchio con un diametro di (x + 2). A = π(d/2) = π((x +2)/2) = ((x +2)/4)π
Calcolo della circonferenza e dell'area di un cerchio
Contenuto
La circonferenza (C) di un cerchio è la sua circonferenza, o la distanza che lo circonda. L`area (A) di un cerchio è quanto spazio occupa il cerchio o l`area racchiusa dal cerchio. Sia l`area che la circonferenza possono essere calcolate con semplici formule dal raggio o diametro del cerchio e dal valore di pi.
Passi
Parte 1 di 3: Calcolo della circonferenza

1. Impara la formula per la circonferenza di un cerchio. Esistono due formule che possono essere utilizzate per calcolare la circonferenza di un cerchio: C = 2πr o C = d, dove π è la costante matematica e approssimativamente uguale a 3,14,R è uguale al raggio e D uguale al diametro.
- Poiché il raggio di un cerchio è uguale al doppio del suo diametro, queste equazioni sono essenzialmente le stesse.
- Le unità per la circonferenza possono essere qualsiasi unità per la misura della lunghezza: chilometri, metri, centimetri, ecc.

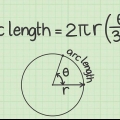
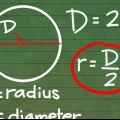
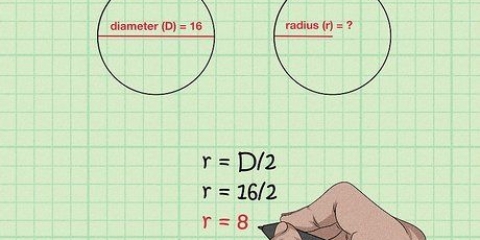
2. Comprendere le diverse parti della formula. Ci sono tre componenti per trovare la circonferenza di un cerchio: raggio, diametro e π. Il raggio e il diametro sono correlati: il raggio è uguale alla metà del diametro, mentre il diametro è uguale al doppio del raggio.

3. Misura il raggio o il diametro del cerchio. Posiziona un righello su un bordo del cerchio, attraverso il centro e sull`altro lato del cerchio. La distanza dal centro del cerchio è il raggio, mentre la distanza dall`altra estremità del cerchio è il diametro.

4. Elaborare e risolvere le variabili. Una volta determinato il raggio e/o il diametro del cerchio, puoi inserire queste variabili nell`equazione appropriata. Se hai il raggio, usa C = 2πr, ma se conosci il diametro, usa C = d.

5. Esercitati con alcuni esempi. Ora che hai imparato la formula, è tempo di esercitarti con alcuni esempi. Più problemi risolverai, più facile sarà risolverli in futuro.
Parte 2 di 3: Area di calcolo

1. Impara la formula per l`area di un cerchio. L`area di un cerchio può essere calcolata utilizzando sia il suo diametro che il suo raggio, con due formule diverse: A = R o A = π(d/2), dove π è la costante matematica approssimativamente uguale a 3,14,R il raggio e D il diametro.
- Poiché il raggio di un cerchio è uguale alla metà del suo diametro, queste equazioni sono essenzialmente le stesse.
- Le unità di superficie possono essere qualsiasi unità di lunghezza al quadrato: km quadrati (km), metri quadrati (m), centimetri quadrati (cm), ecc.

2. Comprendere le diverse parti della formula. Ci sono tre componenti per trovare la circonferenza di un cerchio: raggio, diametro e π. Il raggio e il diametro sono correlati tra loro: il raggio è uguale alla metà del diametro, mentre il diametro è uguale al doppio del raggio.

3. Misura il raggio o il diametro del cerchio. Posiziona un`estremità di un righello in un punto del cerchio, attraverso il centro e sull`altro lato del cerchio. La distanza dal centro del cerchio è il raggio, mentre la distanza dall`altro punto del cerchio è il diametro.

4. Compila le variabili e risolvile. Una volta determinato il raggio e/o il diametro del cerchio, è possibile inserire queste variabili nell`equazione appropriata. Se conosci il raggio, usa A = R, ma se conosci il diametro, usa A = π(d/2).

5. Esercitati con alcuni esempi. Ora che hai imparato la formula, è tempo di esercitarti con alcuni esempi. Più problemi risolverai, più facile sarà risolvere altri problemi.
Parte 3 di 3: Calcolo dell`area e del perimetro con variabili

1. Determina il raggio o il diametro del cerchio. Alcuni problemi danno un raggio o un diametro con una variabile, come r = (x + 7) o d = (x + 3). In questo caso puoi ancora determinare l`area o il perimetro, ma la tua risposta finale conterrà anche quella variabile. Annotare il raggio o il diametro come indicato nella dichiarazione.
- Ad esempio: calcola la circonferenza di una circonferenza di raggio (x = 1).

2. Scrivi la formula con le informazioni fornite. Sia che tu voglia calcolare l`area o il perimetro, segui comunque i passaggi di base per compilare ciò che sai. Scrivi la formula per l`area o il perimetro e poi inserisci le variabili date.

3. Risolvi il problema come se la variabile fosse un numero. A questo punto puoi semplicemente risolvere il problema come faresti normalmente, trattando la variabile come se fosse solo un altro numero. Potrebbe essere necessario il utilizzando la proprietà distributiva per semplificare la risposta finale.

4. Esercitati con alcuni esempi. Ora che hai imparato la formula, è tempo di esercitarti con alcuni esempi. Più problemi risolvi, più facile diventa risolverne di nuovi.
Articoli sull'argomento "Calcolo della circonferenza e dell'area di un cerchio"
Condividi sui social network:
Simile
Popolare