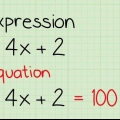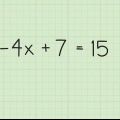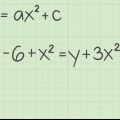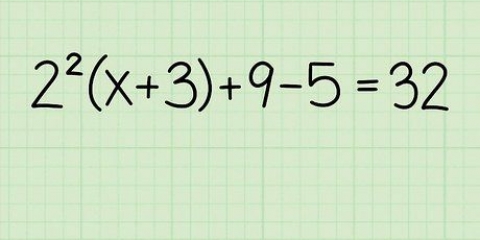Usare la Proprietà Distributiva per Risolvere un'Equazione

Contenuto

Passi
Consigli

La proprietà distributiva è una regola in matematica per semplificare un`equazione con parentesi. Probabilmente hai imparato presto che devi prima eseguire le operazioni tra parentesi, ma con le espressioni algebriche non è sempre possibile. La proprietà distributiva consente di moltiplicare il termine fuori parentesi per i termini al suo interno. Devi stare attento a farlo nel modo giusto, altrimenti potresti perdere informazioni e il confronto non è più corretto. Puoi anche usare la proprietà distributiva per semplificare le equazioni con le frazioni.

Passi

Metodo 1 di 4: utilizzo della proprietà distributiva fondamentale

Immagine titolata Usa proprietà distributiva per risolvere un`equazione Passaggio 1

1. Moltiplica il termine fuori parentesi per qualsiasi termine tra parentesi. Per fare ciò, essenzialmente dividi il termine esterno tra i termini interni. Moltiplica il termine fuori parentesi per il primo termine tra parentesi. Quindi lo moltiplichi per il secondo termine. Se sono presenti più di due termini, continua a distribuire il termine al di fuori delle parentesi tra tutti i termini all`interno delle parentesi. Basta lasciare gli operatori (più o meno) tra parentesi.

$2 (X - 3) = 10$ $2(x-3)=10$
$2 (X) - (2) (3) = 10$ $2(x)-(2)(3)=10$
$2 X - 6 = 10$ $2x-6=10$

Immagine titolata Usa proprietà distributiva per risolvere un`equazione Passaggio 2

2. Combina termini simili. Prima di poter risolvere l`equazione, devi combinare termini simili. Combina tutti i termini numerici tra loro. Inoltre, si combinano separatamente tutti i termini variabili. Per semplificare l`equazione, ordina i termini in modo che le variabili siano su un lato del segno di uguale e le costanti (solo i numeri) siano sull`altro lato.

2 X - 6 = 10

$2x-6=10$ ....(problema originale)

2 X - 6 (+ 6) = 10 (+ 6)

$2x-6(+6)=10(+6)$ .... (aggiungere 6 su entrambi i lati)

2 X = 16

$2x=16$ .... (Variabile sinistra; costante destra)

Immagine titolata Usa proprietà distributiva per risolvere un`equazione Passaggio 3

3. Risolvi l`equazione. sciolto

X

$X$ dividendo entrambi i membri dell`equazione per il coefficiente della variabile.

2 X = 16

$2x=16$ ....(problema originale)

2 X / 2 = 16 / 2

$2x/2=16/2$ ....(dividi entrambi i membri per 2)

X = 8

$x=8$ ....(soluzione)

Metodo 2 di 4: Distribuire coefficienti negativi

Immagine titolata Usa proprietà distributiva per risolvere un`equazione Passaggio 4

1. Distribuisci un numero negativo insieme al segno meno. Se intendi moltiplicare uno o più termini tra parentesi per un numero negativo, assicurati di applicare il segno meno a ciascun termine tra parentesi.

Ricorda le regole di base per moltiplicare per numeri negativi:

Meno x Meno = Più.
Meno x Più = Meno.

Guarda il seguente esempio:

- 4 (9 - 3 X) = 48

$-4(9-3x)=48$ .... (problema originale)

- 4 (9) - (- 4) (3 X) = 48

$-4(9)-(-4)(3x)=48$ ....(moltiplicare -4 per ogni termine)

- 36 - (- 12 X) = 48

$-36-(-12x)=48$ ....(semplificare la moltiplicazione)

- 36 + 12 X = 48

$-36+12x=48$ ....(nota che `meno -12` è uguale a +12)

Immagine titolata Usa proprietà distributiva per risolvere un`equazione Passaggio 5

2. Combina termini simili. Dopo aver completato la distribuzione, è quindi necessario semplificare l`equazione, spostando tutti i termini variabili su un lato del segno di uguale e tutti i numeri senza variabili sull`altro lato. Lo fai per mezzo di una combinazione di addizione o sottrazione.

- 36 + 12 X = 48

$-36+12x=48$ ....(problema originale)

- 36 (+ 36) + 12 X = 48 + 36

$-36(+36)+12x=48+36$ ....(aggiungi 36 per lato)

12 X = 84

$12x=84$ ....(semplificare l`addizione per isolare la variabile)

Immagine titolata Usa proprietà distributiva per risolvere un`equazione Passaggio 6

3. Condividi per ottenere la soluzione finale. Risolvi l`equazione dividendo entrambi i membri dell`equazione per il coefficiente della variabile. Ciò dovrebbe comportare una singola variabile su un lato dell`equazione, con il risultato sull`altro lato.

12 X = 84

$12x=84$ ....(problema originale)

12 X / 12 = 84 / 12

$12x/12=84/12$ ....(dividi entrambi i membri per 12)

X = 7

$x=7$ ....(soluzione)

Immagine titolata Usa proprietà distributiva per risolvere un`equazione Passaggio 7

4. Considera la sottrazione come addizione (da -1). Quando vedi un segno meno in un problema di algebra, specialmente se è prima di una parentesi, essenzialmente dice + (-1). Questo aiuta a distribuire correttamente il segno meno su tutti i termini tra parentesi. Quindi risolvi il problema come prima.

Ad esempio, considera il problema,

4 X - (X + 2) = 4

$4x-(x+2)=4$ . Per assicurarti di aver distribuito correttamente il segno meno, riscrivi il problema in questo modo:

4 X + (- 1) (X + 2) = 4

$4x+(-1)(x+2)=4$

Quindi distribuisci -1 sui termini tra parentesi, come segue:

4 X + (- 1) (X + 2) = 4

$4x+(-1)(x+2)=4$ ....(problema modificato)

4 X - X - 2 = 4

$4x-x-2=4$ ....(moltiplicare -1 per x e per 2)

3 X - 2 = 4

$3x-2=4$ ....(combina i termini)

3 X - 2 + 2 = 4 + 2

$3x-2+2=4+2$ ....(aggiungere 2 su entrambi i lati)

3 X = 6

$3x=6$ ....(semplificare i termini)

3 X / 3 = 6 / 3

$3x/3=6/3$ ....(dividi entrambi i membri per 3)

X = 2

$x=2$ ....(soluzione)

Metodo 3 di 4: utilizzare la proprietà distributiva per semplificare le frazioni

Immagine titolata Usa proprietà distributiva per risolvere un`equazione Passaggio 8

1. Scopri se ci sono coefficienti frazionari o costanti. A volte potrebbe essere necessario risolvere un problema con le frazioni come coefficienti o costanti. Puoi lasciarli così come sono e applicare loro le regole fondamentali dell`algebra, per risolvere il problema. Tuttavia, utilizzando la proprietà distributiva, è spesso possibile semplificare la soluzione convertendo le frazioni in numeri interi.

Dai un`occhiata al seguente esempio $X - 3 = \frac{X}{3} + \frac{1}{6}$ $x-3={frac{x}{3}}+{frac{1}{6}}$ . Le frazioni in questo esempio sono $\frac{X}{3}$ ${frac{x}{3}}$ e $\frac{1}{6}$ ${frac{1}{6}}$ .

Immagine titolata Usa proprietà distributiva per risolvere un`equazione Passaggio 9

2. Trova il minimo comune multiplo (LCM) per tutti i denominatori. A questo punto puoi ignorare tutti i numeri interi. Basta guardare le frazioni e determinare l`LCF per tutti i denominatori. Determina il kgf cercando il numero più piccolo che è un multiplo dei denominatori di entrambe le frazioni nell`equazione. In questo esempio, i denominatori sono 3 e 6, quindi 6 è il kgf.

Immagine titolata Usa la proprietà distributiva per risolvere un`equazione Passaggio 10

3. Moltiplica tutti i termini dell`equazione per kgf. Ricorda, puoi applicare qualsiasi operazione a un`equazione matematica, purché tu lo faccia su entrambi i lati. Moltiplicando ogni termine dell`equazione per lcg i termini si annullano a vicenda e `diventano` interi. Posiziona le parentesi attorno a tutti i lati sinistro e destro dell`equazione, quindi esegui la distribuzione:

X - 3 = \frac{X}{3} + \frac{1}{6}

$x-3={frac{x}{3}}+{frac{1}{6}}$ ....(equazione originale)

(X - 3) = (\frac{X}{3} + \frac{1}{6})

$(x-3)=({frac{x}{3}}+{frac{1}{6}})$ ....(applica parentesi)

6 (X - 3) = 6 (\frac{X}{3} + \frac{1}{6})

$6(x-3)=6({frac{x}{3}}+{frac{1}{6}})$ ....(moltiplicare entrambi i membri per kgf)

6 X - 6 (3) = 6 (\frac{X}{3}) + 6 (\frac{1}{6})

$6x-6(3)=6({frac{x}{3}})+6({frac{1}{6}})$ ....(distribuire la moltiplicazione)

6 X - 18 = 2 X + 1

$6x-18=2x+1$ ....(semplificare la moltiplicazione)

Immagine titolata Usa proprietà distributiva per risolvere un`equazione Passaggio 11

4. Combina termini simili. Combina tutti i termini in modo che tutte le variabili si trovino su un lato dell`equazione e tutte le costanti sull`altro lato. Utilizzare le operazioni di addizione e sottrazione di base per spostare i termini da un lato all`altro dell`equazione.

6 X - 18 = 2 X + 1

$6x-18=2x+1$ ....(problema semplificato)

6 X - 2 X - 18 = 2 X - 2 X + 1

$6x-2x-18=2x-2x+1$ ....(sottrai 2x da entrambi i lati)

4 X - 18 = 1

$4x-18=1$ ....(semplificare meno somma)

4 X - 18 + 18 = 1 + 18

$4x-18+18=1+18$ ....(aggiungere 18 su entrambi i lati)

4 X = 19

$4x=19$ ....(addizione semplificata)

Immagine titolata Usa la proprietà distributiva per risolvere un`equazione Passaggio 12

5. Risolvi l`equazione. Trova la soluzione finale dividendo entrambi i membri dell`equazione per il coefficiente della variabile. Questo ti lascia con x su un lato dell`equazione e la soluzione numerica sull`altro.

4 X = 19

$4x=19$ ....(problema personalizzato)

4 X / 4 = 19 / 4

$4x/4=19/4$ ....(dividi entrambi i lati per 4)

X = \frac{19}{4} o 4 \frac{3}{4}

$x={frac{19}{4}}{text{ o }}4{frac{3}{4}}$ ....(soluzione finale)

Metodo 4 di 4: Distribuisci una frazione con un`equazione

Immagine titolata Usa la proprietà distributiva per risolvere un`equazione Passaggio 13

1. Interpreta una frazione con un`equazione come una divisione distribuita. A volte vedi un problema con più termini nel numeratore di una frazione, al di sopra di un denominatore comune. Devi trattarlo come un problema distributivo e applicare il denominatore a ciascun termine del numeratore. Puoi riscrivere la frazione per mostrare la distribuzione. Come segue:

$4 X + 8 2 = 4$ ${frac{4x+8}{2}}=4$ .....(problema originale)
$4 X 2 + \frac{8}{2} = 4$ ${frac{4x}{2}}+{frac{8}{2}}=4$ .....(moltiplicare il denominatore per ogni termine del numeratore)

Immagine titolata Usa la proprietà distributiva per risolvere un`equazione Passaggio 14

2. Semplifica ogni numeratore come una frazione separata. Dopo aver distribuito il divisore su ogni termine, puoi quindi semplificare ogni termine individualmente.

4 X 2 + \frac{8}{2} = 4

${frac{4x}{2}}+{frac{8}{2}}=4$ .....(problema personalizzato)

2 X + 4 = 4

$2x+4=4$ .....(semplificare le frazioni)

Immagine titolata Usa la proprietà distributiva per risolvere un`equazione Passaggio 15

3. Isola la variabile. Continua a risolvere il problema isolando la variabile su un lato dell`equazione e spostando i termini costanti sull`altro lato. Fallo attraverso una combinazione di addizione e sottrazione, ove necessario.

2 X + 4 = 4

$2x+4=4$ .....(problema personalizzato)

2 X + 4 - 4 = 4 - 4

$2x+4-4=4-4$ .....(sottrai 4 da entrambi i lati)

2 X = 0

$2x=0$ .....(isolare x su un lato)

Immagine titolata Usa proprietà distributiva per risolvere un`equazione Passaggio 16

4. Dividere per il coefficiente per risolvere il problema. Nell`ultimo passaggio dividi per il coefficiente della variabile. Questo dà la soluzione finale, con la singola variabile da un lato dell`equazione e la soluzione numerica dall`altro.

2 X = 0

$2x=0$ .....(problema personalizzato)

2 X / 2 = 0 / 2

$2x/2=0/2$ .....(dividi entrambi i membri per 2)

X = 0

$x=0$ .....(soluzione)

Immagine titolata Usa la proprietà distributiva per risolvere un`equazione Passaggio 17

5. Evita l`errore comune di condividere un solo termine. È allettante (ma scorretto) dividere il primo termine del numeratore per il denominatore ed eliminare la frazione. Un errore come questo sarebbe simile al seguente per il problema precedente:

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(problema originale)

2 X + 8 = 4

$2x+8=4$ .....(solo 4x è diviso per 2, invece del contatore pieno)

2 X + 8 - 8 = 4 - 8

$2x+8-8=4-8$

2 X = - 4

$2x=-4$

X = - 2

$x=-2$ ..... (soluzione sbagliata)

Immagine titolata Usa proprietà distributiva per risolvere un`equazione Passaggio 18

6. Verifica la correttezza della tua soluzione. Puoi sempre controllare il tuo lavoro inserendo la tua soluzione nel problema originale. Quando vuoi semplificare, devi arrivare a una affermazione vera. Se semplifichi e ottieni un`affermazione errata come risposta, la tua soluzione non è corretta. In questo esempio si testano le due soluzioni per x = 0 e x =-2 per vedere quale è corretta.

Inizia con la soluzione x=0:

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(problema originale)

4 (0) + 8 2 = 4

${frac{4(0)+8}{2}}=4$ .....(sostituisci 0 con x)

0 + 8 2 = 4

${frac{0+8}{2}}=4$

\frac{8}{2} = 4

${frac{8}{2}}=4$

4 = 4

$4=4$ .....(Vero. Questa è la soluzione giusta.)

Prova la "soluzione sbagliata per x=-2:

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(problema originale)

4 (- 2) + 8 2 = 4

${frac{4(-2)+8}{2}}=4$ .....(inserisci -2 per x)

- 8 + 8 2 = 4

${frac{-8+8}{2}}=4$

\frac{0}{2} = 4

${frac{0}{2}}=4$

0 = 4

$0=4$ .....(Dichiarazione errata. Pertanto x=-2 è falso.)

Consigli

Puoi anche usare la proprietà distributiva per semplificare alcune moltiplicazioni. Puoi dividere i numeri in decine con un resto per facilitare l`aritmetica mentale. Ad esempio, puoi riscrivere 8 x 16 come 8(10+6). Questo è quindi semplicemente 80 + 48 = 128. Un altro esempio, 7 x 24 = 7(20 + 4) = 7(20) + 7(4) = 140 + 28 = 168. Praticali a memoria e l`aritmetica mentale diventerà molto più facile.