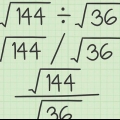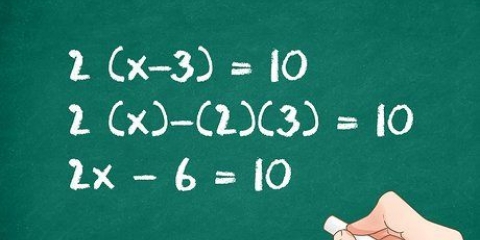Esempio 1: Risolvi:  .
.
Inizia convertendo questo in un logaritmo usando la formula sopra: .
. Questa formula è la formula del "cambio di base", derivata dalle proprietà logaritmiche di base. 
Esempio 1 (segue.): Riscrivi  Se
Se  . Il valore di `?` è la risposta al problema. Potrebbe essere necessario provarne alcuni per trovarlo:
. Il valore di `?` è la risposta al problema. Potrebbe essere necessario provarne alcuni per trovarlo:



16 è quello che stavi cercando, quindi = 4.
= 4. 
Esempio 2: Cos`è  ?
? Convertilo in un logaritmo::  .(Si noti che il 3 scompare in qualsiasi registro iniziale -- questo si applica a qualsiasi base).
.(Si noti che il 3 scompare in qualsiasi registro iniziale -- questo si applica a qualsiasi base). Riscrivi come  e testare possibili valori di ?:
e testare possibili valori di ?:


Dal momento che 58 rientra tra questi due numeri, nessun numero intero come risposta.
nessun numero intero come risposta. Lascia la tua risposta come:  .
. 

Se o x o y è negativo, non c`è soluzione al problema. Se entrambi x se y sono negativi, rimuovi i segni negativi utilizzando la proprietà 
Non ci sono logaritmi di numeri negativi nel problema di esempio, quindi puoi procedere al passaggio successivo. 
Utilizzare questo per espandere il lato sinistro del problema di esempio:

Sostituisci questo nell`equazione originale:

→


Il problema di esempio ha un nuovo termine:  . Poiché 3 = 27, semplifica
. Poiché 3 = 27, semplifica  cattiva 3.
cattiva 3. Il confronto completo è ora:




 .
.
Nel problema di esempio, il n ancora preso nel termine  .
.
Attorno a n per isolare, utilizzare la regola del prodotto dei logaritmi:

Sostituiscilo nell`equazione completa:





Dal 3 = 19683, n = 19683
Condivisione dei logaritmi
Contenuto
I logaritmi possono sembrare difficili da usare, ma proprio come gli esponenti o i polinomi devi solo imparare le tecniche giuste. Hai solo bisogno di conoscere alcune proprietà di base per dividere due logaritmi con la stessa base o per estendere un logaritmo di un quoziente.
Passi
Metodo 1 di 2: Dividere i logaritmi a mano

1. Verifica la presenza di numeri e uno negativi. Questo metodo risolve i problemi nella forma  . Tuttavia, non funziona per alcuni casi speciali:
. Tuttavia, non funziona per alcuni casi speciali:
 . Tuttavia, non funziona per alcuni casi speciali:
. Tuttavia, non funziona per alcuni casi speciali: - Il logaritmo di un numero negativo non è definito per tutte le basi (come
o
). Quindi scrivi "Nessuna soluzione".
- Anche il logaritmo di zero è indefinito per tutte le basi. Se vedi un termine come
, quindi scrivi anche "Nessuna soluzione".
- Il logaritmo di uno in qualsiasi base (
) è sempre uguale a zero, poiché
per tutti i valori di X. Sostituisci quel logaritmo con 1 invece di usare il metodo seguente.
- Se i due logaritmi hanno basi diverse, ad esempio
, e non puoi semplificare nessuno dei due a un numero intero, quindi il problema non può essere risolto a mano.

2. Modifica l`espressione in un logaritmo. Supponendo che tu non abbia trovato nessuna delle eccezioni di cui sopra, ora puoi semplificare il problema in un logaritmo. Per fare ciò, usa la formula .
.
 .
. .
.Inizia convertendo questo in un logaritmo usando la formula sopra:
 .
.
3. Calcolalo a mano, se possibile. Ricorda: oh  per risolvere, pensi a `
per risolvere, pensi a ` ` o `Quale esponente posso usare un elevare a X ottenere?` Non è sempre possibile risolverlo senza una calcolatrice, ma se sei fortunato ti ritroverai con un logaritmo facilmente semplificato.
` o `Quale esponente posso usare un elevare a X ottenere?` Non è sempre possibile risolverlo senza una calcolatrice, ma se sei fortunato ti ritroverai con un logaritmo facilmente semplificato.
 per risolvere, pensi a `
per risolvere, pensi a ` ` o `Quale esponente posso usare un elevare a X ottenere?` Non è sempre possibile risolverlo senza una calcolatrice, ma se sei fortunato ti ritroverai con un logaritmo facilmente semplificato.
` o `Quale esponente posso usare un elevare a X ottenere?` Non è sempre possibile risolverlo senza una calcolatrice, ma se sei fortunato ti ritroverai con un logaritmo facilmente semplificato. Se
Se  . Il valore di `?` è la risposta al problema. Potrebbe essere necessario provarne alcuni per trovarlo:
. Il valore di `?` è la risposta al problema. Potrebbe essere necessario provarne alcuni per trovarlo:


16 è quello che stavi cercando, quindi
 = 4.
= 4.
4. Lascia la risposta in forma logaritmica se non puoi semplificarla. Alcuni logaritmi sono molto difficili da risolvere a mano. Hai bisogno di una calcolatrice se hai bisogno della risposta per uno scopo pratico. Quando risolvi problemi in classe di matematica, il tuo insegnante probabilmente si aspetta che lasci la risposta come logaritmo. Ecco un altro esempio che utilizza questo metodo per un problema più complicato:
 ?
? .(Si noti che il 3 scompare in qualsiasi registro iniziale -- questo si applica a qualsiasi base).
.(Si noti che il 3 scompare in qualsiasi registro iniziale -- questo si applica a qualsiasi base). e testare possibili valori di ?:
e testare possibili valori di ?:

Dal momento che 58 rientra tra questi due numeri,
 nessun numero intero come risposta.
nessun numero intero come risposta. .
.Metodo 2 di 2: Lavorare con il logaritmo di un quoziente

1. Inizia con un problema di divisione in un logaritmo. Questa sezione aiuta a risolvere i problemi con le espressioni nel modulo  .
.
 .
. - Ad esempio, inizia con questo problema:
`Risolvi per n se.`

2. Controlla i numeri negativi. Il logaritmo di un numero negativo non è definito. Se x o y sono un numero negativo, verificare se il problema ha una soluzione prima di continuare:


3. Dividere il quoziente in due logaritmi. Una proprietà utile dei logaritmi è descritta dalla formula:  . In altre parole, il logaritmo di un quoziente è sempre uguale al logaritmo del numeratore, meno il logaritmo del denominatore.
. In altre parole, il logaritmo di un quoziente è sempre uguale al logaritmo del numeratore, meno il logaritmo del denominatore.
 . In altre parole, il logaritmo di un quoziente è sempre uguale al logaritmo del numeratore, meno il logaritmo del denominatore.
. In altre parole, il logaritmo di un quoziente è sempre uguale al logaritmo del numeratore, meno il logaritmo del denominatore.

→


4. Se possibile, semplifica i logaritmi. Se uno qualsiasi dei nuovi logaritmi nell`espressione è un intero, semplificalo ora.
 . Poiché 3 = 27, semplifica
. Poiché 3 = 27, semplifica  cattiva 3.
cattiva 3.

5. Isola la variabile. Come ogni problema di matematica, aiuta a isolare il termine con la variabile su un lato dell`equazione. Elimina termini simili ove possibile per semplificare l`equazione.


 .
.
6. Usa proprietà aggiuntive dei logaritmi quando necessario. Per isolare la variabile da altri termini all`interno dello stesso logaritmo, riscrivi il termine utilizzando diverse proprietà logaritmiche.
 .
.Attorno a n per isolare, utilizzare la regola del prodotto dei logaritmi:





7. Continua a semplificare finché non trovi la soluzione. Ripetere le stesse tecniche algebriche e logaritmiche per risolvere il problema. Se non esiste una soluzione intera, utilizzare una calcolatrice e arrotondare al numero significativo più vicino.


Dal 3 = 19683, n = 19683
Articoli sull'argomento "Condivisione dei logaritmi"
Condividi sui social network:
Popolare