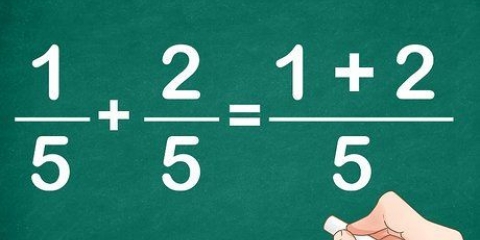A volte i numeri in questa riga avranno un punto decimale, quindi stai effettivamente cercando 2,5 anziché 25. Puoi ignorare questo punto decimale in quanto non influirà sulla tua risposta. Ignora anche qualsiasi punto decimale nel numero di cui vuoi cercare il logaritmo, perché la mantissa per il log di 1.527 non è diversa da quella di 152.7. 














Utilizzo di tabelle logaritmiche
Contenuto
Prima dell`era dei computer e delle calcolatrici, le tabelle venivano utilizzate per calcolare rapidamente i logaritmi, le tabelle dei logaritmi. Queste tabelle possono comunque essere utili per calcolare o moltiplicare rapidamente logaritmi o numeri grandi, una volta capito come usarli.
Passi
Metodo 1 di 3: Lettura di una tabella logaritmica

1. Capire cos`è un logaritmo. 10 fa 100. 10 fa 1000. Le potenze 2 e 3 formano logaritmi con la base 10, o anche il log comune di 100 e 1000. Generalmente, a = c essere riscritto come tronco d`alberounc = b. Così "dieci alla potenza di due fa 100" è l`equivalente di "il log di 100 con base 10 è due." Le tabelle di registro hanno base 10 (usare il registro normale), dove un quindi dovrebbe essere sempre 10.
- Moltiplica due numeri sommando le loro potenze. Ad esempio: 10 * 10 = 10 o 100 * 1000 = 100.000.
- Il ceppo naturale, suggerito da "ln", è il log con base e, dove e è la costante 2.718. Questo è un numero utile per molte aree della matematica e della fisica. Puoi usare le tabelle dei logaritmi naturali allo stesso modo delle normali tabelle dei log, con base 10.

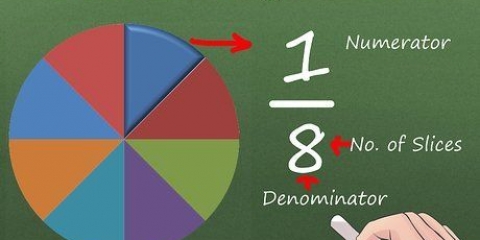
2. Determina le caratteristiche del numero di cui vuoi trovare il logaritmo naturale. 15 è compreso tra 10 (10) e 100 (10), quindi il suo logaritmo sarà compreso tra 1 e 2, se qualcosa come 1 virgola qualcosa. 150 è compreso tra 100 (10) e 1000 (10), quindi il suo logaritmo sarà compreso tra 2 e 3, o qualcosa come 2 virgola qualcosa. La virgola qualcosa si chiama demantisse; questo è ciò che troverai in una tabella di registro. Quello che precede la virgola (punto decimale) (1 nel primo esempio, 2 nel secondo) è il significativo.

3. Fai scorrere il dito verso il basso verso la riga destra della tabella, tramite la colonna all`estrema sinistra. Questa colonna mostrerà le prime due o, per alcune tabelle log di grandi dimensioni, tre cifre del numero di cui stai cercando il logaritmo. Se cerchi il log di 15.27 in una normale tabella di log, vai alla riga 15. Se cerchi il log di 2.57, vai alla riga 25.

4. Nella riga corretta, fai scorrere il dito sulla colonna corretta. Questa colonna è quella contrassegnata dalla cifra successiva del numero di cui stai cercando il logaritmo. Ad esempio, se vuoi trovare il log di 15.27, il tuo dito sarà nella riga 15. Fai scorrere il dito lungo la riga fino alla colonna 2. Ora stai indicando il numero 1818. Annota questo.

5. La tabella di registro ha una tabella di parti proporzionali. Fai scorrere il dito sulla colonna di quella tabella contrassegnata dalla cifra successiva del numero che stai cercando. Per le 15.27 questa cifra è 7. Il tuo dito è ora sulla riga 15 e sulla colonna 2. Passa alla riga 15 e alla colonna delle differenze medie, colonna 7. Ora stai indicando il numero 20. Nota questo.

6. Somma i numeri che hai trovato nei due passaggi precedenti. Per 15.27 ottieni 1838. Questa è la mantissa del logaritmo di 15.27.

7. Aggiungi il significativo. Poiché 15 è compreso tra 10 e 100 (10 e 10), il log di 15 dovrebbe essere compreso tra 1 e 2, quindi 1.qualcosa, quindi il significativo è 1. Combina il significativo con la mantissa per la risposta finale. Quindi il log di 15.27 è 1.1838.
Metodo 2 di 3: Determinazione dell`antilogaritmo

1. Comprendi la tabella antilog. Usalo quando hai il registro di un numero, ma non il numero stesso. Nella formula 10 = x, n è il logaritmo in base 10 comune, o x. Se hai x, puoi trovare n usando la tabella di registro. Se conosci n, determina x usando la tabella antilog.
- L`antilog è anche comunemente noto come log inverso.

2. Nota il significativo. Questo è il numero per la virgola decimale. Se vuoi cercare l`antilog di 2.8699, il significativo è 2. Nella tua mente, rimuovi questo dal numero che stai cercando, ma scrivilo per non dimenticarlo: importerà dopo.

3. Trova la riga corrispondente alla prima parte della mantide1. in 2.8699, la mantissa è 8699. La maggior parte delle tabelle antilog, come la maggior parte delle tabelle dei logaritmi, hanno due numeri nella colonna più a sinistra, quindi usa il dito per seguire la colonna in basso fino ad arrivare a 86.

4. Fai scorrere il dito sulla colonna contrassegnata dal numero successivo della mantissa. Per 2.8699, fai scorrere la riga contrassegnata con .86 per trovare l`intersezione con la colonna 9. Questo dovrebbe darti 7396. Nota questo.

5. Se la tabella antilog ha anche una tabella di parti proporzionali, fai scorrere il dito sulla colonna di quella tabella contrassegnata dalla cifra successiva della mantissa. Assicurati che il tuo dito rimanga nella stessa riga. In questo caso, sposta il dito sull`ultima colonna della tabella, colonna 9. L`intersezione della riga 86 e della colonna 9 con le differenze medie è 15. Nota questo.

6. Somma i due numeri dei due passaggi precedenti insieme. Nel nostro esempio, questi sono 7396 e 15. La somma di entrambi è 7411.

7. Usa il significativo per posizionare il punto decimale. Il significativo era 2. Ciò significa che la risposta dovrebbe essere compresa tra 10 e 10, ovvero tra 100 e 1000. Affinché il numero 7411 rientri tra 100 e 1000, il punto decimale deve essere posizionato dopo tre cifre in modo che il numero sia circa 700, invece di 70, che è troppo piccolo, o 7000, che è troppo grande. Quindi la risposta finale è 741.1.
Metodo 3 di 3: moltiplicare i numeri utilizzando le tabelle di registro

1. Impara come moltiplicare i numeri insieme usando i loro logaritmi. Sappiamo che 10 * 100 = 1000. Scritto in potenze (o logaritmi), diventa 10 * 10 = 10. Sappiamo anche che 1 + 2 = 3. In generale, 10 * 10 = 10. Quindi la somma dei logaritmi di due numeri diversi è il logaritmo del prodotto di questi numeri. Possiamo moltiplicare due numeri con la stessa base sommando le loro potenze.

2. Cerca i logaritmi dei due numeri che vuoi moltiplicare insieme. Usa il metodo sopra per trovare i logaritmi. Ad esempio, se vuoi moltiplicare 15,27 e 48,54 insieme, troverai che il log di 15,27 è uguale a 1,1838 e il log di 48,54 è 1,6861.

3. Somma i due logaritmi e hai trovato il logaritmo della soluzione. In questo esempio, aggiungi 1.1838 e 1.6861 insieme e ottieni 2.8699. Questo numero è il logaritmo della tua risposta.

4. Cerca l`antilogaritmo del risultato dal primo passaggio per trovare la soluzione. Lo fai trovando il numero nella tabella più vicino alla mantissa di questo numero (8699). Tuttavia, un metodo più efficiente e affidabile è trovare la risposta nella tabella degli antilogaritmi, come descritto nel metodo sopra. In questo esempio ottieni 741.1.
Consigli
- Fai sempre i calcoli su un pezzo di carta e non a memoria, poiché si tratta di numeri lunghi e complicati, che possono diventare piuttosto complicati.
- Leggi bene il titolo della pagina. Un libro di logaritmi ha circa 30 pagine e se usi la pagina sbagliata la tua risposta non sarà più corretta.
Avvertenze
- Assicurati di leggere dalla stessa riga. A volte potresti confondere righe e colonne a causa dei numeri piccoli e dell`interlinea breve.
- La maggior parte delle tabelle ha una precisione di 3 o 4 cifre. Se trovi l`antilog di 2,8699 con una calcolatrice, la risposta verrà arrotondata a 741,2, ma la risposta che ottieni con le tabelle di log è 741,1. Ciò è dovuto all`arrotondamento delle tabelle. Se hai bisogno di una risposta più accurata, usa una calcolatrice o qualche altro metodo, piuttosto che le tabelle dei logaritmi.
- Usa i metodi descritti in questo articolo per il registro regolare, o logaritmo in base 10, e assicurati che i numeri che cerchi siano anche in base 10, nota anche come notazione scientifica.
Necessità
- tabella dei logaritmi o libro dei logaritmi
- Carta.
Articoli sull'argomento "Utilizzo di tabelle logaritmiche"
Condividi sui social network:
Popolare