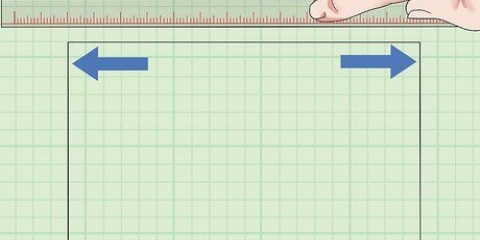
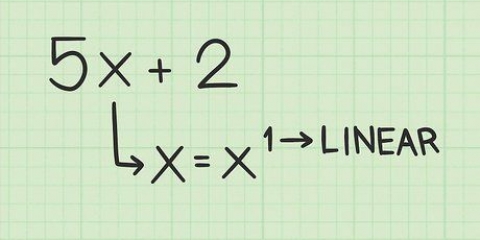Se la mossa ti porta in una "scatola" sopra il quadrato magico, rimani nella colonna di quella casella, ma posiziona il numero nella riga inferiore di quella colonna. Se la mossa ti porta in una casella a destra del quadrato magico, rimani in quella riga, ma posiziona il numero nella colonna di quella riga, all`estrema sinistra del quadrato. Se la mossa ti porta in una casella che ha già un numero, torna alla casella precedente che era stata compilata e posiziona il numero successivo direttamente sopra di essa. 

somma = [6 * (62 + 1)] / 2 somma = [6 * (36 + 1)] / 2 somma = (6 * 37) / 2 somma = 222 / 2 La costante magica di un quadrato 6x6 è 222/2, o 111. Tutte le righe, le colonne e le diagonali devono essere sommate per ottenere questo numero. 
Quindi, per ogni quadrato 6x6, ogni quadrante diventa un quadrato 3x3. 
Nell`esempio di un quadrato 6x6, il quadrante A viene risolto con i numeri da 1 a 9; quadrante B con quelli di 10-18; Quadrante C con 19-27 e Quadrante D con 28-36. 
Tratta il primo numero di ogni quadrante come se fosse uno. Posizionalo nella casella centrale nella riga superiore di ciascun quadrante. Tratta ogni quadrante come un piccolo quadrato magico. Anche se la casella è disponibile in un quadrante adiacente, ignorala e passa alla "regola di eccezione" adatta a questa situazione. 
Usa una matita per segnare tutti i quadrati nella riga superiore fino a raggiungere la casella centrale del quadrante A. Quindi in un quadrato 6x6 segni la casella 1 (con il numero 8), ma in un quadrato 10x10 segni le caselle 1 e 2 (con i numeri 17 e 24, rispettivamente). Segna un quadrato usando le caselle che hai appena contrassegnato come riga superiore. Se hai segnato solo una casella, la tua casella sarà composta da non più di una casella. Chiamiamo questa marcatura A-1. Quindi, in un quadrato magico 10x10, l`indicatore A-1 è composto dalle caselle 1 e 2 nelle righe 1 e 2, creando un quadrato 2x2 nel quadrante in alto a sinistra. Nella riga immediatamente sotto l`indicatore A-1, salta il numero nella prima colonna e quindi contrassegna tutte le caselle da un lato all`altro quante sono state indicate nell`indicatore A-1. Chiamiamo questa riga centrale Marcatura A-2. La selezione A-3 è una casella simile ad A-1, ma posta nell`angolo inferiore sinistro del quadrante. Le selezioni A-1, A-2 e A-3 insieme formano il segnalino A. Ripetere questo processo nel quadrante D, creando un`area marker identica, Marker D. 

Ecco due immagini di un quadrato magico 14x14 prima e dopo entrambi gli interruttori. La superficie di commutazione del quadrante A è contrassegnata in blu, la superficie per il quadrante D è verde, per il quadrante C in giallo e per il quadrante B in arancione. Magic Square di 14x14 prima dell`interruttore (passaggi 6, 7 e 8) Magic Square di 14x14 dopo aver eseguito le sostituzioni (passaggi 6, 7 e 8) 

somma = [4 * (42 + 1)] / 2 somma = [4 * (16 + 1)] / 2 somma = (4 * 17) / 2 somma = 68 / 2 La costante magica di un quadrato 4x4 è 68/2, o 34. Tutte le righe, colonne e diagonali devono formare questo numero. 
In un quadrato 4x4, segna solo i quattro quadrati d`angolo. In un quadrato 8x8, ogni segnalino è un`area 2x2 negli angoli. In un quadrato 12x12, ogni segnalino è un`area 3x3 negli angoli, ecc. 
In un quadrato 4x4, l`indicatore centrale è un`area 2x2 al centro. In un quadrato 8x8, l`indicatore centrale è un`area 4x4 al centro, ecc. 
1 nella casella in alto a sinistra e 4 nella casella in alto a destra 6 e 7 nelle caselle centrali nella riga 2 10 e 11 nelle caselle centrali nella riga 3 13 nella casella in basso a sinistra e 16 nella casella in basso a destra. 
15 e 14 nelle caselle centrali nella riga 1 12 nella casella all`estrema sinistra e 9 nella casella all`estrema destra nella riga 2 8 nella casella all`estrema sinistra e 5 nella casella all`estrema destra nella riga 3 3 e 2 nelle caselle centrali nella riga 4 A questo punto, tutte le colonne, le righe e le diagonali dovrebbero avere una somma uguale alla costante magica calcolata in precedenza.
Risolvi quadrati magici
Contenuto
I quadrati magici sono diventati popolari solo dall`ascesa di giochi basati sulla matematica come Sudoku. Un quadrato magico è una disposizione di numeri in un quadrato in modo tale che la somma di ogni riga, colonna e diagonale sia un numero costante, la cosiddetta costante magica. Questo articolo spiegherà come risolvere qualsiasi tipo di quadrato magico, sia dispari, singolo pari o doppio pari.
Passi
Metodo 1 di 3: Risolvere un quadrato magico dispari

1. Calcola la costante magica. Puoi trovare questo numero usando una semplice formula matematica, dove n = il numero di righe o colonne nel tuo quadrato magico. Quindi, ad esempio, in un quadrato magico 3x3, n = 3. La costante magica = [n * (n2 + 1)] / 2. Quindi nell`esempio del quadrato 3x3:
- somma = [3 * (32 + 1)] / 2
- somma = [3 * (9 + 1)] / 2
- somma = (3 * 10) / 2
- somma = 30 / 2
- La costante magica di un quadrato 3x3 è 30/2, o 15.
- Tutte le righe, colonne e diagonali hanno questo numero come somma.

2. Posiziona il numero 1 nella casella centrale della riga superiore. Questo è sempre il punto da cui inizi se il tuo quadrato magico di lati ha un numero dispari di lati, non importa quanto grande o piccolo sia quel numero. Quindi, se hai un quadrato 3x3, metti il numero 1 nella casella 2; in un quadrato 15x15, posiziona il numero 1 nella casella 8.

3. Inserisci i numeri rimanenti in uno schema da uno a destra. Riempi sempre i numeri secondo una serie (1, 2, 3, 4, ecc.) salendo di una riga e poi di una colonna a destra. Si nota subito che per posizionare il numero 2 si finisce sopra la riga superiore, fuori dal quadrato magico. Va bene, anche se segui sempre il metodo one-up, one-to-right, ci sono tre eccezioni che seguono anche uno schema prevedibile:
Metodo 2 di 3: Risolvere un quadrato magico uniforme semplice

1. Comprendi cos`è un semplice quadrato pari. Tutti sanno che un numero pari è divisibile per 2, ma con i quadrati magici ci sono diversi metodi per risolvere i quadrati pari singoli e doppi.
- Un semplice quadrato pari ha un numero di quadrati per lato divisibile per 2, ma non per 4.
- Il quadrato magico pari più piccolo è 6x6, perché non è possibile creare quadrati magici 2x2.

2. Calcola la costante magica. Usa lo stesso metodo dei quadrati magici dispari: la costante magica = [n * (n2 + 1)] / 2, dove n = il numero di quadrati per lato. Quindi, nell`esempio di un quadrato 6x6:

3. Dividi il quadrato magico in quattro quadranti di uguali dimensioni . Etichettali A (in alto a sinistra), C (in alto a destra), D (in basso a sinistra) e B (in basso a destra). Per determinare quanto deve essere grande ogni quadrato, dividi a metà il numero di caselle in ogni riga o colonna.

4. Assegna un intervallo di numeri a ciascun quadrante. Il quadrante A ottiene un quarto dei numeri; quadrante B il secondo trimestre; Quadrante C il terzo quarto e Quadrante D l`ultimo quarto dell`intervallo numerico totale di un quadrato magico 6x6.

5. Risolvi ogni quadrante usando il metodo del quadrato magico con un numero dispari di caselle per lato. Il quadrante A è facile da compilare poiché inizia con il numero 1, come di solito fanno i quadrati magici. I quadranti B-D, tuttavia, iniziano con numeri dispari: 10, 19 e 28, come nel nostro esempio.

6. Crea i segnalini A e D. Se hai provato ad aggiungere subito colonne, righe e diagonali, hai notato che non si sommano alla costante magica. Dovrai scambiare alcune caselle dei quadranti in alto a sinistra e in basso a sinistra per completare il tuo quadrato magico. Chiamiamo queste aree Marker A e Marker D.

7. Scambia i marker A e D. Questo è uno scambio 1 a 1. Spostare le caselle tra il quadrante A e il quadrante D senza modificare l`ordine. Una volta fatto questo, tutte le righe, colonne e diagonali nel tuo quadrato magico dovrebbero avere la costante magica calcolata in precedenza come somma.

8. Scambia una volta in più per i quadrati magici anche individualmente più grandi di 6x6. Oltre allo switch per i quadranti A e D sopra menzionato, devi anche fare uno switch per i quadranti C e B. Segna le colonne dal lato destro del quadrato a sinistra, una in meno del numero di colonne contrassegnate per l`evidenziazione A-1. Scambia i valori nel quadrante C con i valori nel quadrante B per quelle colonne, usando lo stesso metodo uno a uno.
Metodo 3 di 3: Risolvere un quadrato magico doppio pari

1. Comprendi cos`è un doppio quadrato pari. Un quadrato pari semplice ha un numero di quadrati per lato divisibile per 2. Un quadrato pari doppio ha un numero di quadrati per lato divisibili per 4.
- Il quadrato doppiamente pari più piccolo che può essere realizzato è il quadrato 4x4.

2. Calcola la costante magica. Usa lo stesso metodo dei quadrati magici pari o dispari: la costante magica = [n * (n2 + 1)] / 2, dove n = il numero di quadrati per lato. Quindi, nell`esempio di un quadrato 4x4:

3. Applicare i marcatori A-D. In ogni angolo del quadrato magico, posiziona un quadratino con i lati di n/4, dove n = la lunghezza di un lato dell`intero quadrato magico. In senso antiorario etichettali come Marker A, B, C e D.

4. Posiziona il segno centrale. Segna tutte le caselle al centro del quadrato magico in un`area quadrata di lunghezza n/2, dove n = la lunghezza di ciascun lato di un quadrato magico completo. Il Segnalino Centrale non deve sovrapporsi ai Segnalini A-D, ma deve toccarli negli angoli.

5. Riempi il quadrato magico, ma solo nelle aree contrassegnate. Inizia a riempire i numeri del tuo quadrato magico da sinistra a destra, ma posiziona un numero solo se la casella cade all`interno di un segnalino. Quindi, in una casella 4x4, compila le seguenti caselle:

6. Riempi il resto del quadrato magico contando alla rovescia. Questo è essenzialmente il contrario del passaggio precedente. Ricomincia con la casella in alto a sinistra, ma questa volta salta tutte le caselle che cadono nell`area contrassegnata e riempi le caselle non selezionate contando all`indietro. Inizia con il numero più grande nel tuo intervallo di numeri. Quindi, in un quadrato magico 4x4, compila:
Consigli
- Prova le variazioni su questi passaggi per scoprire i tuoi metodi di soluzione.
Necessità
- Matita
- Carta
- Gomma
Articoli sull'argomento "Risolvi quadrati magici"
Condividi sui social network:
Popolare