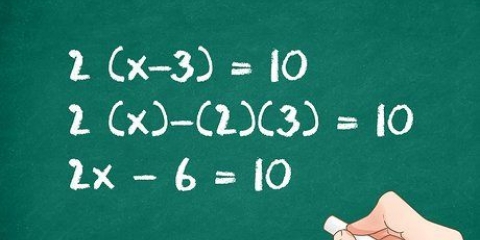4(x+3) + 9 - 5 = 32 
4x + 12 + 9 - 5 = 32 
4x+21-5 = 32 4x+16 = 32 4x + 16 - 16 = 32 - 16 4x = 16 
4x/4 = 16/4 x = 4 
2(x+3)+ 9 - 5 = 32 2(4+3)+ 9 - 5 = 32 2(7) + 9 - 5 = 32 4(7) + 9 - 5 = 32 28 + 9 - 5 = 32 37 - 5 = 32 32 = 32 

2x+12-12 = 44-12 2x = 32 
(2x)/2 = 32/2 x = 16 

2x + 12 = 44 2 x (4) + 12 = 44 2x16 + 12 = 44 32 + 12 = 44 44 = 44 

(x + 3)/6 = 2/3 6 x 2 = 12 (x + 3) x 3 = 3x + 9 3x + 9 = 12 
3x + 9 - 9 = 12 - 9 3x = 3 

(x + 3)/6 = 2/3 (1 + 3)/6 = 2/3 4/6 = 2/3 2/3 = 2/3 

√(2x+9) - 5 + 5 = 0 + 5 √(2x+9) = 5 
(√(2x+9)) = 5 2x + 9 = 25 
2x + 9 - 9 = 25 - 9 2x = 16 

√(2x+9) - 5 = 0 √(2(8)+9) - 5 = 0 √(16+9) - 5 = 0 √(25) - 5 = 0 5 - 5 = 0 

|4x +2| - 6 = 8 |4x +2| - 6 + 6 = 8 + 6 |4x +2| = 14 
4x + 2 = 14 4x + 2 - 2 = 14 -2 4x = 12 x = 3 
4x + 2 = -14 4x + 2 - 2 = -14 - 2 4x = -16 4x/4 = -16/4 x = -4 
(Per x = 3): |4x +2| - 6 = 8 |4(3) +2| - 6 = 8 |12 +2| - 6 = 8 |14| - 6 = 8 14 - 6 = 8 8 = 8 (per x = -4): |4x +2| - 6 = 8 |4(-4) +2| - 6 = 8 |-16 +2| - 6 = 8 |-14| - 6 = 8 14 - 6 = 8 8 = 8
Risolvi x in un'equazione
Contenuto
Esistono diversi modi per risolvere x in un`equazione, sia che tu stia lavorando con esponenti e radici o semplicemente che tu debba dividere o moltiplicare. Qualunque sia il metodo che usi, dovresti sempre trovare un modo per isolare x da un lato dell`equazione in modo da poter calcolare il valore. Ecco come farlo:
Passi
Metodo 1 di 5: utilizzo di un`equazione lineare ordinaria

1. Scrivi il problema. Ecco il compito:
- 2(x+3) + 9 - 5 = 32

2. Calcola l`esponente. Ricorda l`ordine delle operazioni: HMVDOA, che sta per Parentesi, Esponenziazione, Divisione/Moltiplica, Addizione/Sottrazione. In questo caso, non puoi capire prima cosa c`è tra parentesi perché la x appartiene ad essa, quindi inizi con la potenza, 2. 2 = 4

3. Calcola la moltiplicazione. Moltiplica 4 per (x+3). Ecco come:

4. Ora calcola l`addizione e la sottrazione. Basta aggiungere o sottrarre i numeri rimanenti. Ecco come:

5. Isola la variabile. Puoi farlo dividendo entrambi i membri dell`equazione per 4 per trovare x. 4x/4 = x e 16/4 = 4, quindi x = 4.

6. Controlla il tuo calcolo. Sostituisci x = 4 nell`equazione originale per assicurarti che sia corretta. Ecco come:
Metodo 2 di 5: Con esponenziale

1. Scrivi il problema. Supponiamo che tu stia lavorando su un problema in cui il termine x contiene anche un esponente:
- 2x + 12 = 44

2. Isola il termine con l`esponente. La prima cosa che dovresti fare ora è combinare termini simili in modo che tutte le costanti siano sul lato destro dell`equazione mentre il termine con l`esponente sia sulla sinistra. Basta sottrarre 12 da entrambi i lati. Ecco come:

3. Isolare la variabile con l`esponente, dividendo entrambi i membri per il coefficiente del termine x. In questo caso, 2 è il coefficiente x, il che significa che entrambi i membri devono essere divisi per 2 per eliminarlo. Ecco come:

4. Prendi la radice quadrata di ciascun lato dell`equazione. Calcolando la radice quadrata di x, rimani con x a sinistra e la radice quadrata di 16,4, a destra. Quindi, x = 4.

5. Controlla il tuo calcolo. Sostituisci x = 4 nell`equazione originale per assicurarti che sia corretta. Ecco come:
Metodo 3 di 5: Usa le frazioni

1. Scrivi il problema. Supponiamo che tu abbia a che fare con il seguente problema:
- (x + 3)/6 = 2/3

2. Moltiplicazione incrociata. Per moltiplicare in modo incrociato, moltiplica il denominatore di ogni frazione per il numeratore dell`altra frazione. Quindi, moltiplica 6 (il primo denominatore) per 2 (il secondo numeratore), per ottenere 12 sul lato destro dell`equazione.Quindi moltiplica 3 (il secondo denominatore) per x + 3 (il primo numeratore), per ottenere 3 x + 9 a sinistra dell`equazione. Ecco come apparirà:

3. Combina termini simili. Combina le costanti nell`equazione sottraendo 9 da entrambi i lati dell`equazione. Ecco cosa fare:

4. Isola x dividendo ogni termine per il coefficiente x. Basta dividere 3x e 9 per 3, il coefficiente di x, e risolvere per x. 3x/3 = x e 3/3 = 1, quindi rimani con x = 1.

5. Controlla il tuo calcolo. Per controllare il tuo lavoro, sostituisci x nell`equazione originale per assicurarti che sia corretta. Ecco cosa fare:
Metodo 4 di 5: utilizzo dei caratteri radice

1. Scrivi il problema. Supponiamo di risolvere x nel seguente problema:
- √(2x+9) - 5 = 0

2. Isola la radice quadrata. È necessario isolare la parte della radice quadrata dell`equazione a sinistra dell`equazione prima di poter continuare. Quindi aggiungi 5 a entrambi i lati dell`equazione. Ecco come:

3. Disegna la radice quadrata di entrambi i lati. Proprio come dividi entrambi i membri di un`equazione per il coefficiente moltiplicato per x, devi anche prendere la radice quadrata di entrambi i membri di un`equazione se x è inferiore al segno radicale. Questo rimuove il radicale dall`equazione. Ecco come farlo:

4. Combina termini simili. Combina termini uguali sottraendo 9 da entrambi i lati dell`equazione in modo che tutte le costanti siano a destra, mentre x rimane a sinistra. Ecco cosa fare:

5. Isola la variabile. L`ultima cosa da fare per risolvere x è isolare la variabile dividendo entrambi i membri dell`equazione per 2, il coefficiente del termine x. 2x/2 = x e 16/2 = 8, quindi hai x = 8.

6. Controlla il tuo calcolo. Immettere di nuovo 8 nell`equazione per x per verificare che il calcolo sia corretto:
Metodo 5 di 5: utilizzare il valore assoluto

1. Scrivi il problema. Supponiamo che tu stia cercando di risolvere x nel seguente problema:
- |4x +2| - 6 = 8

2. Isola il valore assoluto. La prima cosa da fare è combinare termini simili e isolare il valore assoluto. In questo caso, puoi farlo aggiungendo 6 a entrambi i lati dell`equazione. Ecco come:

3. Rimuovi il valore assoluto e risolvi l`equazione. Questo è il primo e più semplice passo. Ora devi risolvere x due volte, ogni volta che lavori con un valore assoluto. Ecco come farlo la prima volta:

4. Rimuovere il valore assoluto e modificare il segno dei termini sull`altro lato del segno di uguale prima di continuare a risolvere. Ora fallo di nuovo, questa volta rendendo la parte sinistra dell`equazione uguale a -14 invece di 14. Ecco come:

5. Controlla il tuo calcolo. Ora che sai che x = (3, -4), sostituisci entrambi i numeri nell`equazione per assicurarti che sia corretto. Ecco come:
Consigli
- Per controllare il tuo lavoro, inserisci il valore di x nell`equazione originale e risolvilo.
- Le radici sono un altro modo per rappresentare gli esponenti.La radice quadrata di x = x^1/2.
Articoli sull'argomento "Risolvi x in un'equazione"
Condividi sui social network:
Popolare