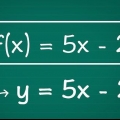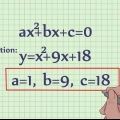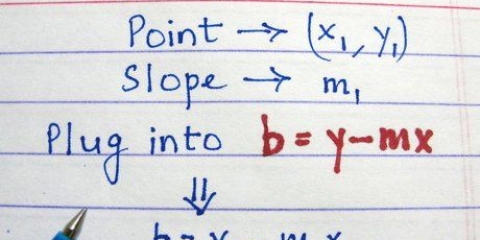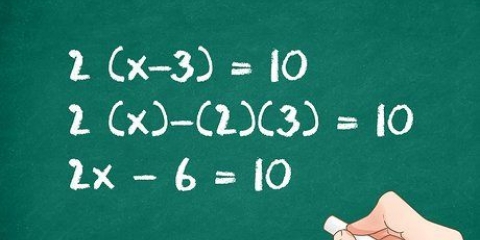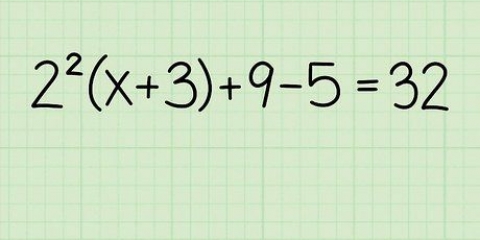Prendi il confronto di esempio  , dove i termini y possono essere spostati a sinistra sottraendo a y da entrambi i lati. Gli altri termini possono essere spostati sul lato destro aggiungendo 6 su entrambi i lati e
, dove i termini y possono essere spostati a sinistra sottraendo a y da entrambi i lati. Gli altri termini possono essere spostati sul lato destro aggiungendo 6 su entrambi i lati e  staccare da entrambi i lati. L`equazione risultante è
staccare da entrambi i lati. L`equazione risultante è  .
. 
Visualizza il confronto di esempio  . Non vi è alcuna limitazione sui valori consentiti di x per questa equazione. Tuttavia, devi renderti conto che questa è l`equazione di una parabola, con x=0 come centro, e una parabola non è una funzione perché non è un confronto uno a uno di valori x e y. Per limitare questa equazione e farne una funzione, per la quale possiamo trovare un`inversa, dobbiamo definire il dominio come x≥0.
. Non vi è alcuna limitazione sui valori consentiti di x per questa equazione. Tuttavia, devi renderti conto che questa è l`equazione di una parabola, con x=0 come centro, e una parabola non è una funzione perché non è un confronto uno a uno di valori x e y. Per limitare questa equazione e farne una funzione, per la quale possiamo trovare un`inversa, dobbiamo definire il dominio come x≥0. La gamma è limitata allo stesso modo. Si noti che il primo termine,  , sarà sempre positivo o 0, per qualsiasi valore di x. Quindi se l`equazione aggiunge +2, l`intervallo sarà qualsiasi valore y≥2.
, sarà sempre positivo o 0, per qualsiasi valore di x. Quindi se l`equazione aggiunge +2, l`intervallo sarà qualsiasi valore y≥2. È necessario definire il dominio e l`ambito in questa fase iniziale. Utilizzerai queste definizioni in seguito per definire il dominio e l`ambito della funzione inversa. Infatti, il dominio della funzione originale diventa l`intervallo della funzione inversa e l`intervallo della funzione originale diventa il dominio dell`inversa. 
Lavorare con il confronto di esempio  , questo passaggio di inversione risulterà nella nuova equazione di
, questo passaggio di inversione risulterà nella nuova equazione di  .
. Un formato alternativo consiste nel sostituire i termini y con x, ma sostituire i termini x con entrambi  o
o  per indicare la funzione inversa.
per indicare la funzione inversa. 
 (premessa originale)
(premessa originale) (sottrai 2 da entrambi i lati)
(sottrai 2 da entrambi i lati) (dividi entrambi i membri per 2)
(dividi entrambi i membri per 2)± (radice quadrata di entrambi i lati; ricorda che la radice quadrata dà possibili risposte sia positive che negative)
(radice quadrata di entrambi i lati; ricorda che la radice quadrata dà possibili risposte sia positive che negative) 
Vedere la soluzione dell`equazione di esempio ± . Poiché la funzione radice quadrata non è definita per valori negativi, il termine deve esserlo
. Poiché la funzione radice quadrata non è definita per valori negativi, il termine deve esserlo  Sii sempre positivo. Pertanto, i valori consentiti di x (il dominio) devono essere x≥2. Con quello come dominio, i valori risultanti di y (l`intervallo) sono tutti i valori y≥0, se prendi la soluzione positiva della radice quadrata, o y≤0, se prendi la soluzione negativa di la radice quadrata. Nota che per trovare la funzione inversa, hai originariamente definito il dominio come x≥0. Pertanto, la soluzione corretta per la funzione inversa è l`opzione positiva.
Sii sempre positivo. Pertanto, i valori consentiti di x (il dominio) devono essere x≥2. Con quello come dominio, i valori risultanti di y (l`intervallo) sono tutti i valori y≥0, se prendi la soluzione positiva della radice quadrata, o y≤0, se prendi la soluzione negativa di la radice quadrata. Nota che per trovare la funzione inversa, hai originariamente definito il dominio come x≥0. Pertanto, la soluzione corretta per la funzione inversa è l`opzione positiva. Confronta il dominio e l`intervallo dell`inverso con il dominio e l`intervallo dell`originale. Ricordalo per la funzione originale,  , il dominio è stato definito come tutti i valori di x≥0 e l`intervallo è stato definito come tutti i valori di y≥2. Per la funzione inversa, ora questi valori si scambiano e il dominio è tutti i valori di x≥2 e l`intervallo è tutti i valori di y≥0.
, il dominio è stato definito come tutti i valori di x≥0 e l`intervallo è stato definito come tutti i valori di y≥2. Per la funzione inversa, ora questi valori si scambiano e il dominio è tutti i valori di x≥2 e l`intervallo è tutti i valori di y≥0. 
Ad esempio, scegli il valore x=1 per l`equazione originale  . Questo dà il risultato y=4.
. Questo dà il risultato y=4. Quindi inserisci il valore 4 nella funzione inversa  . Questo in effetti dà il risultato y=1. Puoi concludere che la tua funzione inversa è corretta.
. Questo in effetti dà il risultato y=1. Puoi concludere che la tua funzione inversa è corretta. 

Si noti che questa forma standard consiste in un termine quadratico perfetto,  , che viene poi modificato dagli altri due elementi a e k. Per arrivare a questa perfetta forma quadratica, dovrai creare determinate condizioni nella tua equazione quadratica.
, che viene poi modificato dagli altri due elementi a e k. Per arrivare a questa perfetta forma quadratica, dovrai creare determinate condizioni nella tua equazione quadratica. 
Per completare il quadrato, lavorare a rovescio. Inizi con  e un secondo x-termine. Dal coefficiente di quel termine, che puoi definire `2b`, devi ricavare
e un secondo x-termine. Dal coefficiente di quel termine, che puoi definire `2b`, devi ricavare  vedere per trovare. Ciò richiede una combinazione di divisione per due e quindi di quadratura del risultato.
vedere per trovare. Ciò richiede una combinazione di divisione per due e quindi di quadratura del risultato. 
Prendi, ad esempio, la funzione quadratica  . Puoi semplificarlo dividendo tutti i termini per 2 per ottenere la funzione risultante
. Puoi semplificarlo dividendo tutti i termini per 2 per ottenere la funzione risultante  ottenere. Il coefficiente 2 rimane fuori dalle parentesi e farà parte della tua soluzione finale.
ottenere. Il coefficiente 2 rimane fuori dalle parentesi e farà parte della tua soluzione finale. Se tutti i termini non sono multipli di a, ottieni coefficienti frazionari. Ad esempio: la funzione  sarà semplificato a
sarà semplificato a  . Calcola attentamente le frazioni.
. Calcola attentamente le frazioni. 
Ad esempio, se i primi due termini della tua funzione quadratica  trovi il terzo termine necessario dividendo 3 per 2 (o 3/2), e poi quadrandolo, per ottenere 9/4. Il quadratico
trovi il terzo termine necessario dividendo 3 per 2 (o 3/2), e poi quadrandolo, per ottenere 9/4. Il quadratico  è un quadrato perfetto.
è un quadrato perfetto. Un altro esempio: supponiamo i primi due termini  sono. La metà del termine medio è -2, quindi lo quadrati per ottenere 4. Il quadrato perfetto risultante è
sono. La metà del termine medio è -2, quindi lo quadrati per ottenere 4. Il quadrato perfetto risultante è  .
. 
Supponiamo di avere la funzione  . Come accennato in precedenza, usi i primi due termini per completare il quadrato. Usando il termine medio di -4x, generi un terzo termine +4. Aggiungi 4 e sottrai 4 dall`equazione, nel modulo
. Come accennato in precedenza, usi i primi due termini per completare il quadrato. Usando il termine medio di -4x, generi un terzo termine +4. Aggiungi 4 e sottrai 4 dall`equazione, nel modulo  . Le parentesi vengono posizionate solo per definire l`equazione quadratica che stai creando. Nota il +4 tra parentesi e il -4 all`esterno. Semplifica i numeri al risultato
. Le parentesi vengono posizionate solo per definire l`equazione quadratica che stai creando. Nota il +4 tra parentesi e il -4 all`esterno. Semplifica i numeri al risultato  .
. 
Si noti che per questa funzione a=1, h=2 e k=5. Il valore di scrivere l`equazione in questa forma è che a, poiché è positivo, ti dice che la parabola è rivolta verso l`alto. I valori (h, k) indicano il vertice in fondo alla parabola, se si vuole rappresentarla graficamente. 
Continua a lavorare con la funzione di anteprima  . Poiché questo è in formato standard, puoi determinare il vertice come x=2, y=5. Quindi per evitare la simmetria, lavori solo con il lato destro del grafico e imposta il dominio se tutti i valori x≥2. Inserendo il valore x=2 nella funzione si restituisce y=5. Puoi vedere che i valori di y aumenteranno all`aumentare di x. Pertanto, l`intervallo di questa equazione è y≥5.
. Poiché questo è in formato standard, puoi determinare il vertice come x=2, y=5. Quindi per evitare la simmetria, lavori solo con il lato destro del grafico e imposta il dominio se tutti i valori x≥2. Inserendo il valore x=2 nella funzione si restituisce y=5. Puoi vedere che i valori di y aumenteranno all`aumentare di x. Pertanto, l`intervallo di questa equazione è y≥5. 
Continua a lavorare con la funzione  . Inserisci x al posto di f(x) e inserisci y (o f(x), se preferisci) al posto di x. Questo dà come una nuova funzione
. Inserisci x al posto di f(x) e inserisci y (o f(x), se preferisci) al posto di x. Questo dà come una nuova funzione  .
. 
 (punto di partenza originale)
(punto di partenza originale) (sottrai 5 da entrambi i lati)
(sottrai 5 da entrambi i lati)± (radice quadrata di entrambi i lati; ricorda che la radice quadrata fornisce possibili risposte sia positive che negative)
(radice quadrata di entrambi i lati; ricorda che la radice quadrata fornisce possibili risposte sia positive che negative) ± (aggiungere 2 su entrambi i lati)
(aggiungere 2 su entrambi i lati) 
Vedere la soluzione dell`equazione di esempio ± . Poiché la funzione radice quadrata non è definita per valori negativi, il termine deve esserlo
. Poiché la funzione radice quadrata non è definita per valori negativi, il termine deve esserlo  Sii sempre positivo. Pertanto, i valori consentiti di x (il dominio) devono essere x≥5. Con quello come dominio, i valori risultanti di y (l`intervallo) sono tutti i valori y≥2 (se prendi la soluzione positiva della radice quadrata) o y≤2 (se scegli la soluzione negativa della radice quadrata). Ricorda che hai originariamente definito il dominio come x≥2, per trovare la funzione inversa. Pertanto, la soluzione corretta per la funzione inversa è l`opzione positiva.
Sii sempre positivo. Pertanto, i valori consentiti di x (il dominio) devono essere x≥5. Con quello come dominio, i valori risultanti di y (l`intervallo) sono tutti i valori y≥2 (se prendi la soluzione positiva della radice quadrata) o y≤2 (se scegli la soluzione negativa della radice quadrata). Ricorda che hai originariamente definito il dominio come x≥2, per trovare la funzione inversa. Pertanto, la soluzione corretta per la funzione inversa è l`opzione positiva. Confronta il dominio e l`intervallo dell`inverso con il dominio e l`intervallo dell`originale. Ricordiamo che per la funzione originale, il dominio era definito come tutti i valori di x≥2, e l`intervallo era definito come tutti i valori di y≥5. Per questa funzione inversa questi valori si scambiano e il dominio è ora tutti i valori di x≥5 e l`intervallo è tutti i valori di y≥2. 
Ad esempio, scegli il valore x=3 da includere nell`equazione originale  processare. Questo dà il risultato y=6.
processare. Questo dà il risultato y=6. Quindi elabori y=6 nella funzione inversa  . Questo restituisce y=3, che è il numero con cui hai iniziato. Puoi concludere che la tua funzione inversa è corretta.
. Questo restituisce y=3, che è il numero con cui hai iniziato. Puoi concludere che la tua funzione inversa è corretta. 

Per questa sezione di questo articolo, utilizzerai l`equazione di esempio  .
. 

Basato sull`equazione del lavoro  , questo dà il risultato
, questo dà il risultato  .
. 
Per l`equazione di esempio, per ottenere il lato sinistro uguale a zero, devi sottrarre x da entrambi i lati dell`equazione. Questo dà il risultato  .
. 
Lasciare  . Quindi, x=1
. Quindi, x=1 Lasciare  . Quindi b=2
. Quindi b=2 Lasciare  . Quindi, c=(-3-x)
. Quindi, c=(-3-x) 
x=[-b±√(b^2-4ac)]/2a x=(-2)±√((-2)^2-4(1)(-3-x)) / 2(1) x=((-2)±√(4+12+4x)))/2 x=(-2±√(16+4x))/2 x=(-2±√(4)(4+x)))/2 x=-2±2√(4+x))/2 x=-1±√(4+x) f-inverse = -1±√(4+x)(Questo ultimo passaggio è possibile perché hai scambiato f(x) con la variabile x in una fase precedente). 




Assumendo la funzione originaria  , scegli il tuo x=-2. Questo restituisce y=-3. Ora sostituisci il valore di x=-3 nella funzione inversa,
, scegli il tuo x=-2. Questo restituisce y=-3. Ora sostituisci il valore di x=-3 nella funzione inversa,  . Questo restituisce -2, che è effettivamente il valore con cui hai iniziato. Quindi la tua definizione della funzione inversa è corretta.
. Questo restituisce -2, che è effettivamente il valore con cui hai iniziato. Quindi la tua definizione della funzione inversa è corretta.
Trovare l'inversa di un'equazione quadratica
Contenuto
Le funzioni inverse possono essere molto utili per risolvere molti problemi di matematica. Essere in grado di prendere una funzione e trovare la sua funzione inversa è uno strumento potente. Tuttavia, con le equazioni quadratiche, questo può essere un processo piuttosto complicato. Per prima cosa è necessario definire accuratamente l`equazione, determinando un dominio e un intervallo appropriati. È quindi possibile scegliere tra tre metodi per calcolare la funzione inversa. La scelta del metodo è principalmente una questione di preferenze personali.
Passi
Metodo 1 di 3: Trovare l`inversa di una funzione semplice

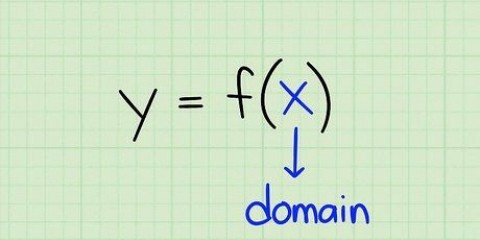
1. Trova una funzione sotto forma di y = un X 2 + C  . Se hai il tipo di funzione "giusto" con cui iniziare, puoi trovare l`inverso con una semplice algebra. Questa forma è una sorta di variazione
. Se hai il tipo di funzione "giusto" con cui iniziare, puoi trovare l`inverso con una semplice algebra. Questa forma è una sorta di variazione  . Se lo confronti con una funzione quadratica standard,
. Se lo confronti con una funzione quadratica standard,  , vedi che il medio termine
, vedi che il medio termine  manca. Un altro modo per dirlo è che il valore di b è zero. Se la tua funzione ha questa forma, trovare l`inverso è abbastanza facile.
manca. Un altro modo per dirlo è che il valore di b è zero. Se la tua funzione ha questa forma, trovare l`inverso è abbastanza facile.
 . Se hai il tipo di funzione "giusto" con cui iniziare, puoi trovare l`inverso con una semplice algebra. Questa forma è una sorta di variazione
. Se hai il tipo di funzione "giusto" con cui iniziare, puoi trovare l`inverso con una semplice algebra. Questa forma è una sorta di variazione  . Se lo confronti con una funzione quadratica standard,
. Se lo confronti con una funzione quadratica standard,  , vedi che il medio termine
, vedi che il medio termine  manca. Un altro modo per dirlo è che il valore di b è zero. Se la tua funzione ha questa forma, trovare l`inverso è abbastanza facile.
manca. Un altro modo per dirlo è che il valore di b è zero. Se la tua funzione ha questa forma, trovare l`inverso è abbastanza facile. - La tua funzione di partenza non deve essere esattamente uguale
. Finché puoi guardarlo e vedere che la funzione consiste solo in
termini e numeri costanti, sarai in grado di utilizzare questo metodo.
- Supponiamo di iniziare con l`equazione
. Un rapido esame di questa equazione rivela che non ci sono termini di
essere alla prima potenza. Questa equazione è un candidato per questo metodo per trovare una funzione inversa.

2. Semplifica combinando termini simili. L`equazione iniziale può avere più termini in una combinazione di addizione e sottrazione. Il tuo primo passo è combinare termini simili per semplificare l`equazione e riscriverla nel formato standard  .
.
 .
. , dove i termini y possono essere spostati a sinistra sottraendo a y da entrambi i lati. Gli altri termini possono essere spostati sul lato destro aggiungendo 6 su entrambi i lati e
, dove i termini y possono essere spostati a sinistra sottraendo a y da entrambi i lati. Gli altri termini possono essere spostati sul lato destro aggiungendo 6 su entrambi i lati e  staccare da entrambi i lati. L`equazione risultante è
staccare da entrambi i lati. L`equazione risultante è  .
.
3. Determinare il dominio e l`intervallo della funzione semplificata. Ricordiamo che il dominio di una funzione è costituito dai possibili valori di x che possono essere applicati per dare una soluzione reale. L`intervallo di una funzione è costituito dai valori di y che verranno restituiti. Per determinare il dominio della funzione, cerca i valori che producono un risultato matematicamente impossibile. Si indica quindi il dominio se tutti gli altri valori di x. Per trovare l`intervallo, considera i valori di y in punti limite arbitrari e osserva il comportamento della funzione.
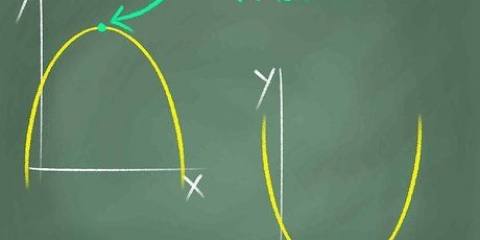
 . Non vi è alcuna limitazione sui valori consentiti di x per questa equazione. Tuttavia, devi renderti conto che questa è l`equazione di una parabola, con x=0 come centro, e una parabola non è una funzione perché non è un confronto uno a uno di valori x e y. Per limitare questa equazione e farne una funzione, per la quale possiamo trovare un`inversa, dobbiamo definire il dominio come x≥0.
. Non vi è alcuna limitazione sui valori consentiti di x per questa equazione. Tuttavia, devi renderti conto che questa è l`equazione di una parabola, con x=0 come centro, e una parabola non è una funzione perché non è un confronto uno a uno di valori x e y. Per limitare questa equazione e farne una funzione, per la quale possiamo trovare un`inversa, dobbiamo definire il dominio come x≥0. , sarà sempre positivo o 0, per qualsiasi valore di x. Quindi se l`equazione aggiunge +2, l`intervallo sarà qualsiasi valore y≥2.
, sarà sempre positivo o 0, per qualsiasi valore di x. Quindi se l`equazione aggiunge +2, l`intervallo sarà qualsiasi valore y≥2.
4. Scambia i ruoli dei termini x e y. Senza modificare l`equazione in altro modo, devi sostituire tutte le forme di y con x e tutte le forme di x con y. Questo è il passaggio che effettivamente "inverte" l`equazione.
 , questo passaggio di inversione risulterà nella nuova equazione di
, questo passaggio di inversione risulterà nella nuova equazione di  .
. o
o  per indicare la funzione inversa.
per indicare la funzione inversa.
5. Riscrivi l`equazione inversa in termini di y. Usando una combinazione di passaggi algebrici e assicurandoti che la stessa operazione venga eseguita su entrambi i lati dell`equazione, dovrai isolare la variabile y. Per il confronto  , questa revisione si presenta così:
, questa revisione si presenta così:
 , questa revisione si presenta così:
, questa revisione si presenta così: (premessa originale)
(premessa originale) (sottrai 2 da entrambi i lati)
(sottrai 2 da entrambi i lati) (dividi entrambi i membri per 2)
(dividi entrambi i membri per 2) (radice quadrata di entrambi i lati; ricorda che la radice quadrata dà possibili risposte sia positive che negative)
(radice quadrata di entrambi i lati; ricorda che la radice quadrata dà possibili risposte sia positive che negative)
6. Determina il dominio e l`intervallo della funzione inversa. Come all`inizio, esamina l`equazione invertita per determinare il dominio e l`intervallo. Con due possibili soluzioni, scegli la soluzione che ha un dominio e un intervallo che sono l`inverso del dominio e dell`intervallo originali.
 . Poiché la funzione radice quadrata non è definita per valori negativi, il termine deve esserlo
. Poiché la funzione radice quadrata non è definita per valori negativi, il termine deve esserlo  Sii sempre positivo. Pertanto, i valori consentiti di x (il dominio) devono essere x≥2. Con quello come dominio, i valori risultanti di y (l`intervallo) sono tutti i valori y≥0, se prendi la soluzione positiva della radice quadrata, o y≤0, se prendi la soluzione negativa di la radice quadrata. Nota che per trovare la funzione inversa, hai originariamente definito il dominio come x≥0. Pertanto, la soluzione corretta per la funzione inversa è l`opzione positiva.
Sii sempre positivo. Pertanto, i valori consentiti di x (il dominio) devono essere x≥2. Con quello come dominio, i valori risultanti di y (l`intervallo) sono tutti i valori y≥0, se prendi la soluzione positiva della radice quadrata, o y≤0, se prendi la soluzione negativa di la radice quadrata. Nota che per trovare la funzione inversa, hai originariamente definito il dominio come x≥0. Pertanto, la soluzione corretta per la funzione inversa è l`opzione positiva. , il dominio è stato definito come tutti i valori di x≥0 e l`intervallo è stato definito come tutti i valori di y≥2. Per la funzione inversa, ora questi valori si scambiano e il dominio è tutti i valori di x≥2 e l`intervallo è tutti i valori di y≥0.
, il dominio è stato definito come tutti i valori di x≥0 e l`intervallo è stato definito come tutti i valori di y≥2. Per la funzione inversa, ora questi valori si scambiano e il dominio è tutti i valori di x≥2 e l`intervallo è tutti i valori di y≥0.
7. Controlla se la tua funzione inversa funziona. Per assicurarti che il tuo lavoro sia corretto e che la tua inversa sia l`equazione corretta, scegli un valore qualsiasi per x e inseriscilo nell`equazione originale per trovare y. Quindi metti quel valore di y al posto di x nella tua equazione inversa e vedi se ottieni il numero con cui hai iniziato. Se è così, la tua funzione inversa è corretta.
 . Questo dà il risultato y=4.
. Questo dà il risultato y=4. . Questo in effetti dà il risultato y=1. Puoi concludere che la tua funzione inversa è corretta.
. Questo in effetti dà il risultato y=1. Puoi concludere che la tua funzione inversa è corretta.Metodo 2 di 3: Completare il quadrato per trovare la funzione inversa

1. Assegna all`equazione quadratica la forma corretta. Per trovare l`inverso, devi iniziare con l`equazione della forma  . Se necessario, è necessario combinare termini simili per ottenere l`equazione in questo formato. Con l`equazione scritta in questo modo, puoi dire qualcosa in più a riguardo.
. Se necessario, è necessario combinare termini simili per ottenere l`equazione in questo formato. Con l`equazione scritta in questo modo, puoi dire qualcosa in più a riguardo.
 . Se necessario, è necessario combinare termini simili per ottenere l`equazione in questo formato. Con l`equazione scritta in questo modo, puoi dire qualcosa in più a riguardo.
. Se necessario, è necessario combinare termini simili per ottenere l`equazione in questo formato. Con l`equazione scritta in questo modo, puoi dire qualcosa in più a riguardo. - La prima cosa che noterai è il valore del coefficiente a. se un>0, quindi l`equazione definisce una parabola le cui estremità puntano verso l`alto (parabola di valle). se un<0, quindi l`equazione definisce una parabola le cui estremità puntano verso il basso (parabola di montagna). Si noti che a≠0. Se non lo fosse, questa sarebbe una funzione lineare e non quadratica.

2. Riconoscere il formato standard del quadratico. Prima di poter trovare la funzione inversa, devi riscrivere l`equazione nel formato standard. Il formato standard per una funzione quadratica è  . I termini numerici a, h e k verranno valutati se si trasforma l`equazione calcolando il quadrato.
. I termini numerici a, h e k verranno valutati se si trasforma l`equazione calcolando il quadrato.
 . I termini numerici a, h e k verranno valutati se si trasforma l`equazione calcolando il quadrato.
. I termini numerici a, h e k verranno valutati se si trasforma l`equazione calcolando il quadrato. , che viene poi modificato dagli altri due elementi a e k. Per arrivare a questa perfetta forma quadratica, dovrai creare determinate condizioni nella tua equazione quadratica.
, che viene poi modificato dagli altri due elementi a e k. Per arrivare a questa perfetta forma quadratica, dovrai creare determinate condizioni nella tua equazione quadratica.
3. Ripensa alla forma di una perfetta funzione quadratica. Ricordiamo che una funzione quadratica che è un quadrato perfetto nasce da due binomi di  , o
, o  . Se fai questa moltiplicazione, ottieni
. Se fai questa moltiplicazione, ottieni  . Quindi il primo termine del quadratico è il primo termine del binomio, al quadrato, e l`ultimo termine del quadratico è il quadrato del secondo termine del binomio. Il termine medio è costituito dal doppio del prodotto dei due termini, in questo caso
. Quindi il primo termine del quadratico è il primo termine del binomio, al quadrato, e l`ultimo termine del quadratico è il quadrato del secondo termine del binomio. Il termine medio è costituito dal doppio del prodotto dei due termini, in questo caso  .
.
 , o
, o  . Se fai questa moltiplicazione, ottieni
. Se fai questa moltiplicazione, ottieni  . Quindi il primo termine del quadratico è il primo termine del binomio, al quadrato, e l`ultimo termine del quadratico è il quadrato del secondo termine del binomio. Il termine medio è costituito dal doppio del prodotto dei due termini, in questo caso
. Quindi il primo termine del quadratico è il primo termine del binomio, al quadrato, e l`ultimo termine del quadratico è il quadrato del secondo termine del binomio. Il termine medio è costituito dal doppio del prodotto dei due termini, in questo caso  .
. e un secondo x-termine. Dal coefficiente di quel termine, che puoi definire `2b`, devi ricavare
e un secondo x-termine. Dal coefficiente di quel termine, che puoi definire `2b`, devi ricavare  vedere per trovare. Ciò richiede una combinazione di divisione per due e quindi di quadratura del risultato.
vedere per trovare. Ciò richiede una combinazione di divisione per due e quindi di quadratura del risultato.
4. Assicurati che il coefficiente di X 2  1 è. Ricordi la forma originale della funzione quadratica
1 è. Ricordi la forma originale della funzione quadratica  . Se il primo coefficiente è diverso da 1, devi dividere tutti i termini per quel valore per ottenere a=1.
. Se il primo coefficiente è diverso da 1, devi dividere tutti i termini per quel valore per ottenere a=1.
 1 è. Ricordi la forma originale della funzione quadratica
1 è. Ricordi la forma originale della funzione quadratica  . Se il primo coefficiente è diverso da 1, devi dividere tutti i termini per quel valore per ottenere a=1.
. Se il primo coefficiente è diverso da 1, devi dividere tutti i termini per quel valore per ottenere a=1. . Puoi semplificarlo dividendo tutti i termini per 2 per ottenere la funzione risultante
. Puoi semplificarlo dividendo tutti i termini per 2 per ottenere la funzione risultante  ottenere. Il coefficiente 2 rimane fuori dalle parentesi e farà parte della tua soluzione finale.
ottenere. Il coefficiente 2 rimane fuori dalle parentesi e farà parte della tua soluzione finale. sarà semplificato a
sarà semplificato a  . Calcola attentamente le frazioni.
. Calcola attentamente le frazioni.
5. Trova la metà del coefficiente medio e quadralo. Hai già i primi due termini della formula quadratica. Questi sono il termine  e il coefficiente che rappresenta il termine x. Prendendo quel coefficiente come valore che ha, puoi aggiungere o sottrarre il numero necessario per creare un quadrato perfetto. Ricordiamo dall`alto che il terzo termine del quadrato richiesto è questo secondo coefficiente diviso per due e poi al quadrato.
e il coefficiente che rappresenta il termine x. Prendendo quel coefficiente come valore che ha, puoi aggiungere o sottrarre il numero necessario per creare un quadrato perfetto. Ricordiamo dall`alto che il terzo termine del quadrato richiesto è questo secondo coefficiente diviso per due e poi al quadrato.
 e il coefficiente che rappresenta il termine x. Prendendo quel coefficiente come valore che ha, puoi aggiungere o sottrarre il numero necessario per creare un quadrato perfetto. Ricordiamo dall`alto che il terzo termine del quadrato richiesto è questo secondo coefficiente diviso per due e poi al quadrato.
e il coefficiente che rappresenta il termine x. Prendendo quel coefficiente come valore che ha, puoi aggiungere o sottrarre il numero necessario per creare un quadrato perfetto. Ricordiamo dall`alto che il terzo termine del quadrato richiesto è questo secondo coefficiente diviso per due e poi al quadrato. trovi il terzo termine necessario dividendo 3 per 2 (o 3/2), e poi quadrandolo, per ottenere 9/4. Il quadratico
trovi il terzo termine necessario dividendo 3 per 2 (o 3/2), e poi quadrandolo, per ottenere 9/4. Il quadratico  è un quadrato perfetto.
è un quadrato perfetto. sono. La metà del termine medio è -2, quindi lo quadrati per ottenere 4. Il quadrato perfetto risultante è
sono. La metà del termine medio è -2, quindi lo quadrati per ottenere 4. Il quadrato perfetto risultante è  .
.
6. Aggiungi e sottrai contemporaneamente dal terzo termine richiesto. Questo è un concetto complicato, ma funziona. L`aggiunta e la sottrazione dello stesso numero in punti diversi della funzione non cambia realmente il valore della funzione. Tuttavia, in questo modo otterrai la tua funzione nella forma corretta.
 . Come accennato in precedenza, usi i primi due termini per completare il quadrato. Usando il termine medio di -4x, generi un terzo termine +4. Aggiungi 4 e sottrai 4 dall`equazione, nel modulo
. Come accennato in precedenza, usi i primi due termini per completare il quadrato. Usando il termine medio di -4x, generi un terzo termine +4. Aggiungi 4 e sottrai 4 dall`equazione, nel modulo  . Le parentesi vengono posizionate solo per definire l`equazione quadratica che stai creando. Nota il +4 tra parentesi e il -4 all`esterno. Semplifica i numeri al risultato
. Le parentesi vengono posizionate solo per definire l`equazione quadratica che stai creando. Nota il +4 tra parentesi e il -4 all`esterno. Semplifica i numeri al risultato  .
.
7. Fattorizzare l`equazione quadratica. Il polinomio tra parentesi è un`equazione quadratica, che puoi riscrivere come  . Nell`esempio del passaggio precedente (
. Nell`esempio del passaggio precedente ( ) si calcola il fattore quadratico
) si calcola il fattore quadratico  . Copia il resto dell`equazione in modo che la tua soluzione
. Copia il resto dell`equazione in modo che la tua soluzione  sta diventando. Questa è la stessa funzione dell`equazione quadratica originale (
sta diventando. Questa è la stessa funzione dell`equazione quadratica originale ( ), riscritto come modulo standard
), riscritto come modulo standard  .
.
 . Nell`esempio del passaggio precedente (
. Nell`esempio del passaggio precedente ( ) si calcola il fattore quadratico
) si calcola il fattore quadratico  . Copia il resto dell`equazione in modo che la tua soluzione
. Copia il resto dell`equazione in modo che la tua soluzione  sta diventando. Questa è la stessa funzione dell`equazione quadratica originale (
sta diventando. Questa è la stessa funzione dell`equazione quadratica originale ( ), riscritto come modulo standard
), riscritto come modulo standard  .
.
8. Definire il dominio e l`ambito della funzione. Il dominio è l`insieme di valori x che possono essere utilizzati come input per la funzione. L`intervallo è l`insieme dei valori y che possono essere il risultato. Ricordiamo che una parabola non è una funzione con un inverso definibile, perché non esiste una relazione uno-a-uno tra i valori x e i valori y, a causa della simmetria della parabola. Per risolvere questo problema, devi definire il dominio come tutti i valori di x maggiori di x=h, il vertice della parabola.
 . Poiché questo è in formato standard, puoi determinare il vertice come x=2, y=5. Quindi per evitare la simmetria, lavori solo con il lato destro del grafico e imposta il dominio se tutti i valori x≥2. Inserendo il valore x=2 nella funzione si restituisce y=5. Puoi vedere che i valori di y aumenteranno all`aumentare di x. Pertanto, l`intervallo di questa equazione è y≥5.
. Poiché questo è in formato standard, puoi determinare il vertice come x=2, y=5. Quindi per evitare la simmetria, lavori solo con il lato destro del grafico e imposta il dominio se tutti i valori x≥2. Inserendo il valore x=2 nella funzione si restituisce y=5. Puoi vedere che i valori di y aumenteranno all`aumentare di x. Pertanto, l`intervallo di questa equazione è y≥5.
9. Scambia i valori xey. Questo è il passaggio in cui inizi trovando la forma inversa dell`equazione. Lascia l`equazione nella sua interezza tranne lo scambio di queste variabili.
 . Inserisci x al posto di f(x) e inserisci y (o f(x), se preferisci) al posto di x. Questo dà come una nuova funzione
. Inserisci x al posto di f(x) e inserisci y (o f(x), se preferisci) al posto di x. Questo dà come una nuova funzione  .
.
10. Riscrivi l`equazione inversa in termini di y. Utilizzando una combinazione di passaggi algebrici, assicurandosi di eseguire la stessa operazione in modo uniforme su entrambi i lati dell`equazione, isolare la variabile y. Per il confronto dei lavori  questa revisione si presenta così:
questa revisione si presenta così:
 questa revisione si presenta così:
questa revisione si presenta così: (punto di partenza originale)
(punto di partenza originale) (sottrai 5 da entrambi i lati)
(sottrai 5 da entrambi i lati) (radice quadrata di entrambi i lati; ricorda che la radice quadrata fornisce possibili risposte sia positive che negative)
(radice quadrata di entrambi i lati; ricorda che la radice quadrata fornisce possibili risposte sia positive che negative) (aggiungere 2 su entrambi i lati)
(aggiungere 2 su entrambi i lati)
11. Determina il dominio e l`intervallo della funzione inversa. Come all`inizio, esamina l`equazione inversa per determinare il dominio e l`intervallo. Con due possibili soluzioni, scegli la soluzione che ha un dominio e un intervallo che sono l`inverso del dominio e dell`intervallo originali.
 . Poiché la funzione radice quadrata non è definita per valori negativi, il termine deve esserlo
. Poiché la funzione radice quadrata non è definita per valori negativi, il termine deve esserlo  Sii sempre positivo. Pertanto, i valori consentiti di x (il dominio) devono essere x≥5. Con quello come dominio, i valori risultanti di y (l`intervallo) sono tutti i valori y≥2 (se prendi la soluzione positiva della radice quadrata) o y≤2 (se scegli la soluzione negativa della radice quadrata). Ricorda che hai originariamente definito il dominio come x≥2, per trovare la funzione inversa. Pertanto, la soluzione corretta per la funzione inversa è l`opzione positiva.
Sii sempre positivo. Pertanto, i valori consentiti di x (il dominio) devono essere x≥5. Con quello come dominio, i valori risultanti di y (l`intervallo) sono tutti i valori y≥2 (se prendi la soluzione positiva della radice quadrata) o y≤2 (se scegli la soluzione negativa della radice quadrata). Ricorda che hai originariamente definito il dominio come x≥2, per trovare la funzione inversa. Pertanto, la soluzione corretta per la funzione inversa è l`opzione positiva.
12. Controlla se la tua funzione inversa funziona. Per assicurarti che il tuo lavoro sia corretto e che la tua inversa sia l`equazione corretta, scegli un valore qualsiasi per x e inseriscilo nell`equazione originale per trovare y. Quindi metti quel valore di y al posto di x nella tua equazione inversa e vedi se ottieni il numero con cui hai iniziato. Se sì, allora la tua funzione inversa è corretta.
 processare. Questo dà il risultato y=6.
processare. Questo dà il risultato y=6. . Questo restituisce y=3, che è il numero con cui hai iniziato. Puoi concludere che la tua funzione inversa è corretta.
. Questo restituisce y=3, che è il numero con cui hai iniziato. Puoi concludere che la tua funzione inversa è corretta.Metodo 3 di 3: utilizzo della formula quadrata

1. Usa la formula quadratica per risolvere x. Ricorda, quando si risolvono equazioni quadratiche, esiste un metodo per calcolarle (se possibile). Se la fattorizzazione non funzionasse, potresti usare la formula quadrata, che darebbe le soluzioni reali a qualsiasi equazione quadratica. Puoi anche usare la formula quadrata come metodo per trovare funzioni inverse.
- La formula quadrata è x=[-b±√(b^2-4ac)]/2a.
- Si noti che la formula del quadrato fornisce due possibili soluzioni, una positiva e una negativa. Farai questa scelta in base alla determinazione del dominio e dell`ambito della funzione.

2. Inizia con un`equazione quadratica per trovare l`inversa. La tua equazione quadratica dovrebbe iniziare nel formato  . Esegui i passaggi algebrici necessari per ottenere la tua equazione in quella forma.
. Esegui i passaggi algebrici necessari per ottenere la tua equazione in quella forma.
 . Esegui i passaggi algebrici necessari per ottenere la tua equazione in quella forma.
. Esegui i passaggi algebrici necessari per ottenere la tua equazione in quella forma. .
.
3. Traccia l`equazione per determinare il dominio e l`intervallo. Tracciare la funzione utilizzando una calcolatrice grafica o tracciando diversi punti fino a poter disegnare la parabola. Vedrai che questa equazione definisce una parabola con il punto più alto in (-1,-4). Quindi per definire questa come una funzione che avrà un inverso, definisci il dominio come tutti i valori di x≤-1. L`intervallo è quindi tutti i valori y≥-4.

4. Scambia le variabili x e y. Per trovare l`inverso, scambia le variabili x e y. Lascia l`equazione invariata, tranne scambiare le variabili. A questo punto, sostituisci x con f(x).
 , questo dà il risultato
, questo dà il risultato  .
.
5. Imposta il lato sinistro dell`equazione uguale a zero. Ricorda che per utilizzare la formula quadratica devi impostare l`equazione uguale a zero, quindi utilizzare i coefficienti nella formula. Allo stesso modo, questo metodo per trovare una funzione inversa inizia impostando l`equazione uguale a zero.
 .
.
6. Ridefinire le variabili per adattarle alla formula quadrata. Questo passaggio è un po` complicato. Sappi che la formula del quadrato risolve x, nell`equazione  . Quindi, per l`equazione che hai ora,
. Quindi, per l`equazione che hai ora,  , per conformarsi a tale classificazione, è necessario ridefinire i termini come segue:
, per conformarsi a tale classificazione, è necessario ridefinire i termini come segue:
 . Quindi, per l`equazione che hai ora,
. Quindi, per l`equazione che hai ora,  , per conformarsi a tale classificazione, è necessario ridefinire i termini come segue:
, per conformarsi a tale classificazione, è necessario ridefinire i termini come segue: . Quindi, x=1
. Quindi, x=1 . Quindi b=2
. Quindi b=2 . Quindi, c=(-3-x)
. Quindi, c=(-3-x)
7. Risolvi la formula quadrata con questi valori ridefiniti. Normalmente elabori i valori di a, b e c nella formula quadrata per risolvere x. Tuttavia, ricorda che in precedenza hai scambiato xey per trovare la funzione inversa. Quindi, quando usi la formula del quadrato per risolvere x, stai effettivamente risolvendo y o l`inversa f. I passaggi per risolvere la formula del quadrato funzionano come segue:

8. Scrivi le due possibili soluzioni. Si noti che la formula del quadrato fornisce due possibili risultati, utilizzando il simbolo ±. Scrivi le due soluzioni separate per facilitare la determinazione del dominio e dell`intervallo e fornire la soluzione finale corretta. Queste due soluzioni sono:



9. Determina il dominio e l`intervallo della funzione inversa. Si noti che per definire la radice quadrata, il dominio deve essere x≥-4. Ricordiamo che il dominio della funzione originale era x≤-1 e l`intervallo era y≥-4. Per scegliere la funzione inversa che corrisponde, è necessaria la seconda soluzione,  scegliere come funzione inversa corretta.
scegliere come funzione inversa corretta.
 scegliere come funzione inversa corretta.
scegliere come funzione inversa corretta.
10. Controlla se la tua funzione inversa è corretta. Per assicurarti che il tuo lavoro sia corretto e che la tua inversa sia l`equazione corretta, scegli un valore qualsiasi per x e inseriscilo nell`equazione originale per trovare y. Quindi metti quel valore di y al posto di x nella tua equazione inversa e vedi se ottieni il numero con cui hai iniziato. Se sì, allora la tua funzione inversa è corretta.
 , scegli il tuo x=-2. Questo restituisce y=-3. Ora sostituisci il valore di x=-3 nella funzione inversa,
, scegli il tuo x=-2. Questo restituisce y=-3. Ora sostituisci il valore di x=-3 nella funzione inversa,  . Questo restituisce -2, che è effettivamente il valore con cui hai iniziato. Quindi la tua definizione della funzione inversa è corretta.
. Questo restituisce -2, che è effettivamente il valore con cui hai iniziato. Quindi la tua definizione della funzione inversa è corretta.Articoli sull'argomento "Trovare l'inversa di un'equazione quadratica"
Condividi sui social network:
Simile
Popolare