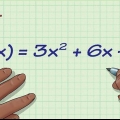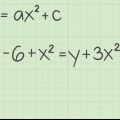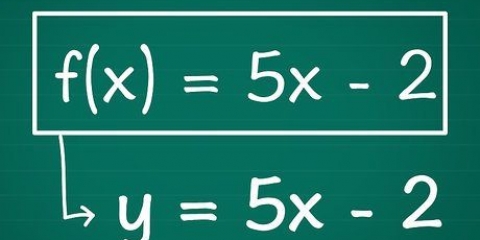Se il valore di un è positivo, allora si ottiene il valore minimo, perché la parabola in alto è aperta (il vertice è il punto più basso del grafico).
Se il valore di un è negativo, troverai il valore massimo, perché la parabola in basso è aperta (il vertice è il punto più alto del grafico).
Il valore di un non può essere zero, altrimenti non abbiamo a che fare con un`equazione quadratica, giusto?







Determinazione dei valori massimo e minimo di una funzione quadratica
Contenuto
La coordinata y della cresta o della valle di una parabola (normalmente rappresentata da k) è anche il valore massimo o minimo dell`equazione quadratica rappresentata dalla parabola. Vediamo come determinarlo!
Passi
Metodo 1 di 4: Per un`equazione quadratica della forma y = ax + bx + c

1. Decidi se vuoi determinare il valore massimo o il valore minimo. È l`uno o l`altro, non puoi fare entrambi.
- Il valore massimo o minimo di un`equazione quadratica è lo stesso del picco o della valle di quella funzione.
La funzione y = ax + bx + c,
(c - b/4a) restituisce il valore y (il valore della funzione) come vertice.




Metodo 2 di 4: Per un`equazione quadratica nella forma y = a(x-h) + k

1. Per y = a(x-h) + k, K è il valore della funzione al vertice.
- K ci dà il valore massimo o minimo dell`equazione quadratica quando un è rispettivamente negativo o positivo.

Metodo 3 di 4: Differenziare su un`equazione quadratica della forma y = ax^2 + bx + c

1. Differenzia y per x. dy/dx = 2ax + b

2. Determina quali sono i valori derivati in termini di dy/dx. Poiché dy/dx è la funzione derivata di una curva, la derivata di una curva può essere determinata in qualsiasi momento. Il valore massimo/minimo può quindi essere determinato impostando questi valori pari a 0, e quindi determinando i valori corrispondenti. dy/dx = 0, 2ax+b = 0, x = -b/2a

3. Sostituisci questo valore di x in y per il valore minimo/massimo.
Metodo 4 di 4: Esempi

1. Determina il valore massimo o minimo della funzione f(x) = x + x + 1.

2. Determina il valore massimo o minimo della funzione f(x) = -2(x-1) + 3.
Consigli
- L`asse di simmetria della parabola è x = h.
- -h è il valore corrispondente al valore massimo o minimo.
Articoli sull'argomento "Determinazione dei valori massimo e minimo di una funzione quadratica"
Condividi sui social network:
Simile
Popolare