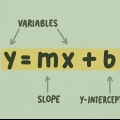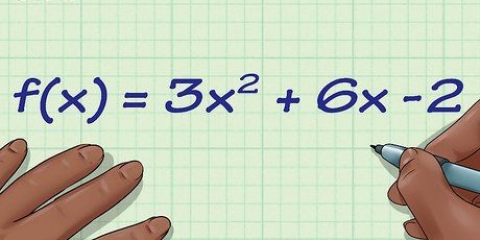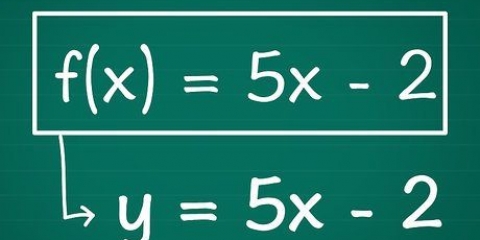Come Disegnare il Grafico di una Funzione

Contenuto

Passi
Consigli

Un grafico di una funzione è una rappresentazione visiva del comportamento di una funzione su un piano x-y. I grafici ci aiutano a comprendere vari aspetti della funzione che sarebbero difficili da comprendere solo osservando la funzione stessa. Puoi rappresentare graficamente migliaia di equazioni e ci sono formule diverse per ogni equazione. Tuttavia, ci sono sempre modi per rappresentare graficamente una funzione se hai dimenticato i passaggi esatti per il tipo specifico di funzione.

Passi

Metodo 1 di 3: tracciare un`equazione lineare con una tangente

Immagine titolata Graph a Function Step 1

1. Sappi che le funzioni lineari sono linee semplici facili da disegnare, come y=2X+5{ displaystyle y=2x+5} ${ displaystyle y=2x+5}$ . C`è una variabile e una costante, scritte come

F (X) o F y = un + B X

${ displaystyle F (x) ofy = a + bx}$ in una funzione lineare, senza esponenti, radicali, ecc. Se hai un`equazione così semplice, anche il grafico della funzione è semplice. Altri esempi di funzioni lineari sono:

$F (n) = 4 - 2 n$ ${ displaystyle F (n) = 4-2 n}$
$y = 3 T - 120$ ${ displaystyle y = 3t-120}$
$F (X) = \frac{2}{3} X + 3$ ${displaystyle F(x)={frac {2}{3}}x+3}$

Immagine titolata Graph a Function Step 2

2. Utilizzare la costante per indicare l`intersezione con l`asse y. L`intersezione con l`asse y è il punto in cui la funzione incrocia l`asse y sul grafico. In altre parole, è il punto in cui

X = 0

${displaystyle x=0}$ . Quindi, per trovarlo, imposta x su zero e lascia la costante nell`equazione. Nell`esempio precedente,

y = 2 X + 5

${ displaystyle y=2x+5}$ , è l`intersezione con l`asse y uguale a y=5, cioè il punto (0.5). Segna questo punto sul grafico con un punto.

Immagine titolata Graph a Function Step 3

3. Trova la pendenza della tua linea con il numero appena prima della variabile. Nell`esempio,

y = 2 X + 5

${ displaystyle y=2x+5}$ , è la pendenza `2`. Questo perché 2 appartiene alla variabile `x`. La pendenza indica quanto è ripida una linea o quanto è alta la linea prima di girare a destra oa sinistra. Una pendenza maggiore significa una linea più ripida.

Immagine titolata Graph a Function Step 4

4. Fai una frazione della pendenza. La pendenza ha a che fare con la pendenza e la pendenza è semplicemente la differenza tra il movimento su e giù e sinistra e destra. La pendenza è una frazione di la variazione di y rispetto alla variazione di x. Quanto deve "cambiare su y" la linea prima di "cambiare su x"? Nell`esempio, la pendenza `2` può essere letta come

2 o m h o o G 1 A destra

${displaystyle {frac {2{text{ }}su}{1{text{ a destra}}}}}$ .

Se la pendenza è negativa, significa che la linea scende quando si va a destra.

Immagine titolata Graph a Function Step 5

5. Inizia dall`intersezione con l`asse y e segui le modifiche su y e x, per disegnare più punti. Una volta che conosci la pendenza, usala per disegnare la tua funzione lineare. Inizia dall`intersezione con l`asse y, qui (0,5), quindi sali 2 e 1 a destra. Segnare anche questo punto (1,7). Trova altri 1-2 punti per disegnare il grafico.

Immagine titolata Graph a Function Step 6

6. Usa un righello per collegare i tuoi punti e rappresentare graficamente la tua funzione lineare. Per evitare errori o grafici approssimativi, trova e collega almeno tre punti separati, anche se due saranno sufficienti in caso di emergenza. Questo è il grafico della tua equazione lineare!

Metodo 2 di 3: Stima dei punti su un grafico

Immagine titolata Graph a Function Step 7

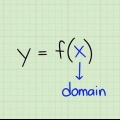
1. Determina la funzione. Assumere la funzione del modulo F(X), vero y rappresenta l`intervallo, X rappresenta il dominio, e F la funzione. Come esempio usiamo y = x+2, per cui F(X) = x+2.

Immagine titolata Graph a Function Step 8

2. Disegna due linee incrociate su un foglio di carta. La linea orizzontale sei tu X-cenere. La linea verticale sei tu y-cenere.

Immagine titolata Graph a Function Step 9

3. Numera il tuo grafico. Evidenzia entrambi i X-come se il y-asse con numeri equidistanti tra loro. Per il X-asse sono i numeri positivi a destra e negativi a sinistra. Per il y-asse sono i numeri positivi in alto e negativi in basso.

Immagine titolata Graph a Function Step 10

4. Calcola un y-valore per 2-3 X-i valori. Assume la funzione F(X) = x+2. Calcola alcuni valori per y dai valori corrispondenti per X visibile sull`asse nella funzione. Per equazioni più complicate può essere necessario semplificare la funzione, isolando prima una variabile.

-1: -1 + 2 = 1

0: 0 +2 = 2

1: 1 + 2 = 3

Immagine titolata Graph a Function Step 11

5. Disegna il punto del grafico per ogni coppia. Disegna linee verticali sottili immaginarie lungo il X-asse e orizzontalmente lungo il y-cenere. Il punto in cui queste linee si intersecano è un punto grafico (o usa semplicemente carta millimetrata).

Immagine titolata Graph a Function Step 12

6. Elimina le linee immaginarie. Dopo aver disegnato tutti i punti del grafico, puoi cancellare le linee immaginarie. Nota: il grafico di f(x) = x sarebbe una retta ad esso parallela attraverso l`origine (0,0), ma f(x) = x+2 è spostato di due unità (lungo l`asse y) sulla griglia a causa del +2 nell`equazione.

Metodo 3 di 3: Rappresentazione grafica di una funzione complessa

Immagine titolata Graph a Function Step 13

1. Comprendere come rappresentare graficamente tipi comuni di equazioni. Esistono tante diverse strategie di creazione di grafici quanti sono i tipi di funzioni, troppe per essere completamente trattate qui. Se trovi questo difficile e un preventivo non funziona, dai un`occhiata agli articoli su:

Funzioni quadratiche
Funzioni razionali
Funzioni logaritmiche
Disuguaglianze (nessuna caratteristica, ma comunque informazioni utili).

Immagine titolata Graph a Function Step 14

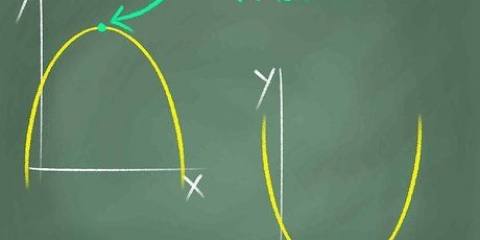
2.Per prima cosa determina gli zeri. Gli zeri sono i punti in cui il grafico interseca la linea orizzontale sul grafico. Sebbene non tutti i grafici abbiano zeri, la maggior parte lo fa ed è il primo passo che devi compiere per fare tutto bene. Per trovare gli zeri, prima imposta l`intera funzione su zero, quindi risolvila. Ad esempio:

F (X) = 2 X 2 - 18

${displaystyle F(x)=2x^{2}-18}$

Rendi F(x) uguale a zero:

0 = 2 X 2 - 18

${displaystyle 0=2x^{2}-18}$

Risolvere:

0 = 2 X 2 - 18

${displaystyle 0=2x^{2}-18}$

18 = 2 X 2

${displaystyle 18=2x^{2}}$

9 = X 2

${displaystyle 9=x^{2}}$

X = 3, - 3

${displaystyle x=3,-3}$

Immagine titolata Graph a Function Step 15

3. Trova e contrassegna eventuali asintoti orizzontali (luoghi in cui la funzione è impossibile da raggiungere) con una linea tratteggiata. Di solito sono punti in cui il grafico non esiste, ad esempio dove dividi per zero. Se la tua equazione ha una variabile in una frazione, ad esempio

y = 1 4 - X 2

${displaystyle y={frac {1}{4-x^{2}}}}$ , quindi inizia azzerando il fondo della frazione. Puoi mappare tutti i luoghi in cui è uguale a zero (in questo esempio una linea tratteggiata a x=2 e x=-2), perché non puoi mai dividere per zero. Tuttavia, le frazioni non sono gli unici posti in cui trovare gli asintoti. Di solito tutto ciò che serve è un po` di buon senso:

Alcune funzioni quadratiche, come

F (n) = n 2

${displaystyle F(n)=n^{2}}$ non sono mai negativi. Quindi c`è un asintoto a 0.

A meno che tu non stia lavorando con numeri immaginari, questo non è possibile:

\sqrt{- 1}

${displaystyle {sqrt {-1}}}$

Le equazioni con esponenti complessi possono avere molti asintoti.

Immagine titolata Graph a Function Step 16

4. Applica i valori e disegna punti diversi. Basta scegliere alcuni valori per x e risolvere la funzione. Quindi traccia un grafico dei punti sul tuo grafico. Più complicato è il grafico, più punti sono necessari. In generale, -1, 0 e 1 sono i punti più facili da ottenere, anche se vorrai averne due o tre in più su entrambi i lati dello zero per ottenere un buon grafico.

Per il confronto

y = 5 X 2 + 6

${displaystyle y=5x^{2}+6}$ , potresti inserire -1, 0, 1, -2, 2, -10 e 10. Questo ti dà una bella gamma di numeri da confrontare.

Sii intelligente nella selezione dei numeri. Nell`esempio, noti rapidamente che un segno negativo non ha importanza, ad esempio puoi interrompere il test -10, perché sarà lo stesso di 10.

Immagine titolata Graph a Function Step 17

5. Mappa il comportamento finale della funzione per vedere cosa succede quando diventa davvero grande. Questo ti dà un`idea della direzione generale di una funzione, solitamente come a verticale asintoto. Ad esempio: lo sai

y = X 2

${displaystyle y=x^{2}}$ alla fine diventa molto, molto grande. Solo una "x" in più (un milione contro un milione e uno) rende y molto più grande. Esistono alcuni modi per testare il comportamento finale, tra cui:

Assumi da due a quattro valori grandi per x, metà negativo e metà positivo, e disegna i punti.

Cosa succede se inserisci `infinito` per una variabile? La funzione diventa infinitamente più grande o più piccola?

Se i gradi sono uguali in una frazione, ad esempio

F (X) = X 3 - 2 X 3 + 4

${displaystyle F(x)={frac {x^{3}}{-2x^{3}+4}}}$ , quindi dividi solo i primi due coefficienti (

1 - 2

${displaystyle {frac {1}{-2}}}$ per ottenere il tuo asintoto finale (-0,5).

Se i gradi in una frazione sono diversi, dividi l`equazione al numeratore per l`equazione al denominatore usando la divisione lunga del polinomio.

Immagine titolata Graph a Function Step 18

6. Collega i punti, evitando comportamenti asintotici e finali, per stimare il grafico. Una volta che hai cinque o sei punti, gli asintoti e un`idea generale del comportamento finale, usa tutti questi per costruire una versione approssimativa del grafico.

Immagine titolata Graph a Function Step 19

7. Fornisci grafici perfetti usando una calcolatrice grafica. Le calcolatrici grafiche sono potenti computer palmari in grado di fornire grafici esatti per qualsiasi equazione. Consentono di localizzare punti esatti, trovare linee di pendenza e visualizzare facilmente equazioni difficili. Basta inserire l`equazione esatta nella sezione del grafico (di solito un pulsante etichettato `F(x) = `) e premere il pulsante del grafico per avere un`idea della funzione.

Consigli

Le calcolatrici grafiche sono un ottimo modo per esercitarsi. Prova a creare un grafico a mano e poi usa la calcolatrice per ottenere un`immagine perfetta del grafico, quindi confronta entrambi i grafici.
Se davvero non sai più cosa fare, inserisci solo alcuni punti. Fondamentalmente potresti disegnare l`intera funzione in questo modo, se provassi un numero infinito di combinazioni di numeri.