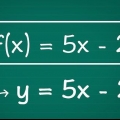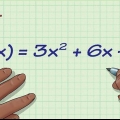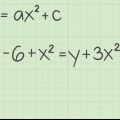Un polinomio senza radici o frazioni con variabili al denominatore. Il dominio di questo tipo di funzione è costituito dall`insieme di tutti i numeri reali. Una funzione con una frazione con una variabile al denominatore. Per trovare il dominio di questo tipo di funzione, poni il denominatore della frazione uguale a zero e ignora il valore x che trovi dopo aver risolto l`equazione. Una funzione con una variabile all`interno di un radicale. Per trovare il dominio di questo tipo di funzione, imposta i termini all`interno del radicale maggiore di 0 e risolvi l`equazione per scoprire quali valori per x sono corretti all`interno di questa funzione. Una funzione con un logaritmo naturale (ln). Scrivi i termini tra parentesi >0 e risolvi. Un grafico. Dedurre dal grafico quali valori sono corretti per x. Un rapporto. Questa è una lista di coordinate xey. Il tuo dominio è semplicemente un elenco di coordinate x. 
La struttura di un dominio è una parentesi quadra/tonda aperta, seguita dai 2 estremi del dominio separati da una virgola e seguita da una parentesi quadra/tonda di chiusura. Ad esempio: [-1.5). Ciò significa che il dominio va da -1 a 5. Usa parentesi quadre come [ e ] per indicare se un numero rientra in un determinato dominio. Quindi nell`esempio, [-1.5), -1 rientra nel dominio. Usa parentesi come ( e ) per indicare che un numero è al di fuori di un determinato dominio. Quindi nell`esempio, [-1.5), il 5 è al di fuori del dominio. Il dominio si ferma in qualsiasi momento prima del 5, ad esempio 4.999.. Usa "U" (significato "unione") per collegare parti del dominio separate tra loro.` Ad esempio: [-1,5) U (5,10]. Ciò significa che il dominio va da -1 a 10, ma c`è un gap nel dominio a 5. Ad esempio, ciò potrebbe essere dovuto a una funzione con "x - 5" al denominatore. puoi fare così tanto "VOI"-utilizzare i simboli se necessario, se il dominio ha più interruzioni. Usa il simbolo dell`infinito (in direzione positiva e negativa) per indicare che in quella direzione il dominio è infinito. All`infinito, usa sempre ( ) e non [ ]. 

f(x) = 2x/(x - 4) x - 4 = 0 (x - 2 )(x + 2) = 0 x ≠ (2, - 2) 
x = tutti i numeri reali tranne 2 e -2 

x-7 0 
x 7 
D = [7,∞) 
Ora controlla l`area sotto -2 (ad es. -3), se questo dà un risultato maggiore di zero. Giusto. (-3) - 4 = 5 Ora controlla l`area tra -2 e 2. Ad esempio, prendi 0. 0 - 4 = -4, quindi sai che i numeri tra -2 e 2 non funzionano. Ora prova un numero superiore a 2, ad esempio +3. 3 - 4 = 5, quindi i numeri sopra 2 funzionano. Annota il dominio quando hai finito. Ecco come scriverlo: D = (-∞, -2) U (2, ∞) 

x - 8 > 0 
x - 8 + 8 > 0 + 8 X > 8 
D = (8,∞) 

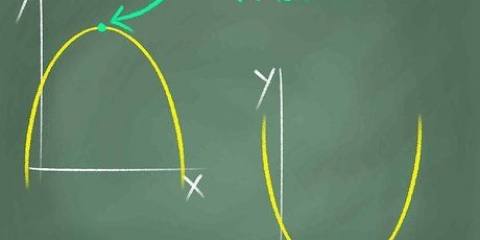
Una linea. Se vedi una linea sul grafico che va all`infinito, alla fine ogni valore di x sarà contenuto nella parabola, quindi il dominio è uguale a tutti i numeri reali. Una normale parabola. Se vedi una parabola rivolta verso l`alto o verso il basso, allora il dominio è costituito da tutti i numeri reali, perché tutti i numeri sull`asse x sono in definitiva contenuti nella parabola. Una parabola orizzontale. Se hai a che fare con una parabola con il vertice in (4,0) che si estende infinitamente a destra, allora il tuo dominio è uguale a D = [4,∞) 




Trovare il dominio di una funzione
Contenuto
- Passi
- Metodo 1 di 6: apprendimento delle basi
- Metodo 2 di 6: Trovare il dominio di una funzione che contiene una frazione
- Metodo 3 di 6: Trovare il dominio di una funzione con radice quadrata
- Metodo 4 di 6: Trovare il dominio di una funzione usando il logaritmo naturale
- Metodo 5 di 6: Trovare il dominio di una funzione usando un grafico
- Metodo 6 di 6: determinazione del dominio di una funzione utilizzando una raccolta/relazione
Il dominio di una funzione è una raccolta di numeri che si adattano a quella funzione. In altre parole, è una raccolta di valori x associati a una data equazione. Viene chiamato l`insieme dei valori y gamma di funzioni. Se desideri sapere come trovare il dominio di una funzione in diverse situazioni, segui questi passaggi.
Passi
Metodo 1 di 6: apprendimento delle basi

1. Impara la definizione di un dominio. Un dominio di una funzione è definito come l`insieme di tutti i numeri reali che possono fungere da input per quella funzione. In altre parole, un dominio è l`insieme completo di valori x immessi in una funzione, che risulta in un insieme di valori y.

2. Scopri come trovare il dominio di diverse funzioni. Il tipo di funzionalità determinerà il metodo migliore per trovare un dominio. Ecco le basi di cui avrai bisogno per le seguenti funzioni:

3. Comprendere la notazione di un dominio. La corretta notazione di un dominio è facile da imparare, ma è importante che tu lo faccia correttamente per non perdere punti in test ed esami. Ecco alcune cose che devi sapere per scrivere correttamente il dominio di una funzione:
Metodo 2 di 6: Trovare il dominio di una funzione che contiene una frazione

1. Scrivi il compito. Supponiamo di avere il seguente problema:
- f(x) = 2x/(x - 4)

2. Per le frazioni con una variabile al denominatore, impostare questa variabile uguale a zero in un`equazione. Se vuoi trovare il dominio di una funzione con una frazione, escludi tutti i valori x che rendono il denominatore uguale a zero, perché non puoi mai dividere per zero. Quindi scrivi il denominatore come un`equazione e ponilo uguale a 0. Ecco come farlo:

3. Prendi nota del dominio. Ecco come farlo:
Metodo 3 di 6: Trovare il dominio di una funzione con radice quadrata

1. Scrivi il compito. Supponiamo di avere il seguente problema: Y = (x-7)

2. Assicurati che i termini all`interno della radice quadrata possano essere maggiori o uguali a 0. Non puoi prendere la radice quadrata di un numero negativo, ma puoi prendere la radice quadrata di zero. Nota che questo vale non solo per le radici quadrate, ma per tutti i numeri di radice pari. Non si applica ai numeri radicali dispari, perché non è un problema se c`è un numero negativo sotto il segno del radicale. Ecco un esempio:

3. Isola la variabile. Ora per separare x sul lato sinistro dell`equazione, aggiungi 7 a entrambi i lati del segno di uguale, in modo che dopo questa operazione assomigli a questo:

4. Scrivi il dominio correttamente. Questa è la notazione corretta:

5. Trova il dominio di una funzione con radice quadrata se sono possibili più soluzioni. Supponiamo di avere la seguente funzione: y = 1/√( ̅x -4). Se prendi il denominatore fuori dalle parentesi e lo rendi uguale a zero ottieni x ≠ (2, - 2). Ecco come procedere:
Metodo 4 di 6: Trovare il dominio di una funzione usando il logaritmo naturale

1. Scrivi il compito. Supponiamo di avere questo:
- f(x) = ln(x-8)

2. Rendi i termini tra parentesi maggiori di zero. Il logaritmo naturale deve essere positivo, quindi rendi i termini tra parentesi maggiori di zero. Ecco un esempio:

3. Risolvere. Separa la variabile x aggiungendo 8 a entrambi i lati dell`equazione. Ecco come:

4. Prendi nota del dominio. Mostra che il dominio di questa equazione è uguale a tutti i numeri maggiori di 8 fino all`infinito. Ecco come:
Metodo 5 di 6: Trovare il dominio di una funzione usando un grafico

1. Visualizza il grafico.

2. Indagare quali valori x appartengono al grafico. Questo è più facile a dirsi che a farsi, quindi ecco alcuni suggerimenti:

3. Determina il dominio. Determina il dominio in base al tipo di grafico che hai. Se non sei del tutto sicuro ma conosci l`equazione della retta, inserisci le coordinate x nella funzione per verificare.
Metodo 6 di 6: determinazione del dominio di una funzione utilizzando una raccolta/relazione

1. Scrivi la relazione. Una relazione è semplicemente una serie di coordinate xey. Supponiamo di avere le seguenti coordinate: {(1, 3), (2, 4), (5, 7)}

2. Scrivi le coordinate x. Questi sono: 1, 2, 5.

3. Determina il dominio. D = {1, 2, 5}

4. Assicurati che questa relazione sia una funzione. Una relazione è una funzione se ogni volta che inserisci una coordinata x numerica ottieni la stessa coordinata y come risposta. Quindi se metti un 3 davanti a x, ottieni 6 come valore y e così via. La prossima relazione è non una funzione perché ottieni due diversi valori y per ogni valore di "X": {(1, 4),(3, 5),(1, 5)}.
Articoli sull'argomento "Trovare il dominio di una funzione"
Condividi sui social network:
Simile
Popolare