Quindi elaborare -1 nella funzione per ottenere la coordinata y. f(-1) = 3(-1) + 6(-1) -2 = 3 - 6 -2 = -5. Il vertice della parabola è (-1,-5). Elaboralo nel grafico disegnando un punto in corrispondenza della coordinata x -1 e della coordinata y -5. Dovrebbe trovarsi nel terzo quadrante del grafico. 
f(-2) = 3(-2) + 6(-2) -2 = -2. Un punto sul grafico è (-2, -2) f(0) = 3(0) + 6(0) -2 = -2. Un altro punto del grafico è (0,-2) f(1) = 3(1) + 6(1) -2 = 7. Un terzo punto del grafico è (1, 7). 



Ma supponiamo che y = -3 sia il punto più basso del grafico, ma che salga per sempre. Allora l`intervallo è f(x) ≥ -3, e non di più. Supponiamo che il grafico raggiunga il suo punto più alto a y=10, ma poi continui a cadere per sempre. Allora l`intervallo è f(x) ≤ 10. 






Ad esempio: se lei vende 2 biglietti dovrai moltiplicare 2 per 5, con 10 come risposta, e quindi l`importo totale raccolto. 

Cioè, qualsiasi numero intero positivo multiplo di cinque è un possibile risultato della funzione.
Determinazione dell'ambito di una funzione
Contenuto
- Passi
- Metodo 1 di 4: Determinazione dell`intervallo di una funzione con una data equazione
- Metodo 2 di 4: Determinazione dell`intervallo di una funzione utilizzando un grafico
- Metodo 3 di 4: Determinazione dell`ambito della funzione di una relazione
- Metodo 4 di 4: Determina l`ambito di una funzione in un problema
- Consigli
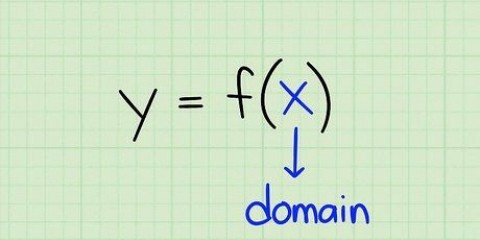
L`intervallo di una funzione è l`insieme di numeri che la funzione può produrre. In altre parole, è l`insieme di valori y che ottieni quando fattori tutti i possibili valori x nella funzione. Questo insieme di valori x è chiamato dominio. Se vuoi sapere come calcolare l`intervallo di una funzione, segui i passaggi seguenti.
Passi
Metodo 1 di 4: Determinazione dell`intervallo di una funzione con una data equazione

1. Scrivi l`equazione. Supponiamo di avere la seguente equazione: f(x) = 3x + 6x -2. Ciò significa che quando si immette un valore per il X dell`equazione, che quindi hai a y-ottiene valore. Questa è la funzione di una parabola.

2. Trova il vertice della funzione, se è un`equazione quadratica. Se hai una retta o qualsiasi funzione con un polinomio o un numero dispari, come f(x) = 6x+2x + 7, puoi saltare questo passaggio. Ma se hai a che fare con una parabola o un`equazione in cui la coordinata x è al quadrato o aumentata di una potenza pari, dovrai disegnare il vertice della parabola. Per fare ciò, usa l`equazione -b/2a per la coordinata x della funzione 3x + 6x -2, dove 3 = a, 6 = b e -2 = c. In questo caso, -B è -6 e 2a è 6, quindi la coordinata x è -6/6 o -1.

3. Trova altri punti della funzione. Per avere un`idea della funzione, dovresti inserire alcuni altri valori per x in modo da poter avere un`idea di come appare la funzione prima di iniziare a cercare l`intervallo. Poiché è una parabola e x è positivo, la parabola punterà verso l`alto (parabola a valle). Ma solo per essere sicuri, inseriamo qualche valore in più per x per vedere quali coordinate y producono:

4. Trova l`intervallo del grafico. Ora guarda le coordinate y sul grafico e trova il punto più basso in cui il grafico tocca la coordinata y. In questo caso la coordinata y più bassa è nella parte superiore della parabola, -5 e il grafico si estende all`infinito oltre questo punto. Ciò significa che l`intervallo della funzione y = tutti i numeri reali ≥ -5.
Metodo 2 di 4: Determinazione dell`intervallo di una funzione utilizzando un grafico

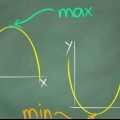
1. Trova il minimo della funzione. Trova la coordinata y più bassa della funzione. Supponiamo che la funzione raggiunga il suo punto più basso a -3. Questa funzione può diventare sempre più piccola, fino all`infinito, quindi non ha un punto più basso fisso, solo l`infinito.

2. Trova il massimo della funzione. Supponiamo che la coordinata y più alta della funzione sia 10. Questa funzione può anche diventare infinitamente più grande, quindi non ha un punto più alto fisso - solo infinita.

3. Indica qual è l`intervallo. Ciò significa che l`intervallo della funzione, o l`intervallo delle coordinate y, è compreso tra -3 e 10. Quindi, -3 ≤ f(x) ≤ 10. Questo è lo scopo della funzione.
Metodo 3 di 4: Determinazione dell`ambito della funzione di una relazione

1. Scrivi la relazione. Una relazione è un insieme di coppie ordinate di coordinate xey. È possibile esaminare una relazione e determinarne il dominio e l`ambito. Supponiamo di avere a che fare con la seguente relazione: {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}.

2. Elenca le coordinate y della relazione. Per determinare l`intervallo della relazione, scriviamo tutte le coordinate y di ciascuna coppia ordinata: {-3, 6, -1, 6, 3}.

3. Rimuovi tutte le coordinate duplicate in modo da avere solo una di ciascuna coordinata y. Potresti aver notato che hai il "6" due volte nell`elenco. Rimuovilo in modo da rimanere con {-3, -1, 6, 3}.

4. Scrivi l`intervallo della relazione in ordine crescente. Quindi disponi i numeri nel set dal più piccolo al più grande e hai trovato l`intervallo. L`intervallo della relazione {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} è {-3,-1, 3, 6}. Siete a posto.

5. Rendi la relazione una funzione è. Affinché una relazione sia una funzione, ogni volta che inserisci un numero da una coordinata x, la coordinata y deve essere la stessa. Ad esempio, la relazione {(2, 3) (2, 4) (6, 9)} è no funzione, perché se inserisci 2 come x per la prima volta, ottieni un 3 come valore, ma la seconda volta inserisci un 2, ottieni quattro. Una relazione è solo una funzione se ottieni sempre lo stesso output per un determinato input. Se inserisci -7, dovresti sempre ottenere la stessa coordinata y (qualunque essa sia), ogni volta.
Metodo 4 di 4: Determina l`ambito di una funzione in un problema

1. Leggi il problema. Supponiamo di lavorare sul seguente problema: "Becky vende i biglietti per il talent show della sua scuola a $ 5 ciascuno. L`importo totale che raccoglie è una funzione del numero di biglietti che vende. Qual è l`intervallo della funzione?"

2. Scrivi il problema come una funzione. In questo caso m l`importo che è stato raccolto e T il numero di biglietti venduti. Poiché ogni biglietto costa 5 euro, dovrai moltiplicare per 5 il numero di biglietti venduti per ottenere l`importo totale. Pertanto, la funzione può essere scritta come M(t) = 5t.

3. Determina qual è il dominio. Per trovare l`intervallo è necessario prima il dominio. Il dominio è costituito da tutti i possibili valori di t che partecipano all`equazione. In questo caso Becky può vendere 0 o più biglietti – non può vendere un numero negativo di biglietti. Dal momento che non conosciamo il numero di posti nell`auditorium della scuola, possiamo supporre che in teoria possa vendere un numero infinito di biglietti. E può vendere solo biglietti interi, non parte di essi. Pertanto, il dominio della funzione T = qualsiasi numero intero positivo.

4. Determina qual è l`intervallo. L`intervallo è il possibile importo che Becky può aumentare con la vendita. Dovrai lavorare con il dominio per trovare l`intervallo. Se sai che il dominio è costituito da un numero intero positivo e che l`equazione M(t) = 5t quindi sai anche che puoi inserire qualsiasi numero intero positivo in questa funzione per la risposta o intervallo. Ad esempio: se vende 5 biglietti, M(5) = 5 x 5 o 25 euro. Se ne vende 100, M(100) = 5 x 100 o 500 euro. Pertanto, l`intervallo della funzione qualsiasi numero intero positivo multiplo di cinque.
Consigli
- Vedi se riesci a trovare l`inverso della funzione. Il dominio dell`inversa di una funzione è uguale all`intervallo di quella funzione.
- Nei casi più difficili può essere più semplice tracciare prima il grafico utilizzando il dominio (se necessario) e poi leggere l`intervallo dal grafico.
- Verificare se la funzione si ripete. Qualsiasi funzione che si ripete lungo l`asse x avrà lo stesso intervallo per l`intera funzione. Ad esempio: f(x) = sin(x) ha un intervallo compreso tra -1 e 1.
Articoli sull'argomento "Determinazione dell'ambito di una funzione"
Condividi sui social network:
Simile
Popolare