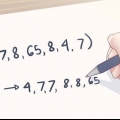Determinazione dell'Interquartile

Contenuto

Passi
Consigli

L`intervallo interquartile viene utilizzato per calcolare la diffusione di un set di dati. L`intervallo interquartile viene utilizzato nelle analisi statistiche per trarre conclusioni su un set di dati. Spesso si preferisce calcolare l`intervallo interquartile piuttosto che l`intervallo, perché la maggior parte dei valori anomali non viene inclusa. Continua a leggere per scoprire come determinare l`intervallo interquartile.

Passi

Metodo 1 di 3: Comprensione dell`intervallo interquartile

1. Comprendere come viene utilizzato l`intervallo interquartile. È essenzialmente un modo per comprendere la distribuzione di un set di dati. L`intervallo interquartile è la differenza tra il quartile più alto (il 25% più alto) e il quartile più basso (il 25% più basso) di un set di dati. Il quartile più basso è solitamente contrassegnato con Q1 e il quartile più alto con Q3, rendendo teoricamente Q2 il centro del set di dati e Q4 il punto più alto.

2. Capire cosa sono i quartili. Per visualizzare un quartile, dividi un elenco di numeri in quattro parti uguali. Ognuna di queste parti è a "quartile." Dai un`occhiata al seguente set di dati: 1, 2, 3, 4, 5, 6, 7, 8.

1 e 2 formano il primo quartile, o Q1.

3 e 4 formano il secondo quartile, o Q2.

5 e 6 formano il terzo quartile, o Q3.

7 e 8 formano il quarto quartile, o Q4.

3. Impara la formula. Per trovare la differenza tra il quartile più alto e quello più basso, sottrarre il 75° percentile dal 25° percentile. La formula è scritta come segue: Q3 – Q1 = intervallo interquartile.

Metodo 2 di 3: Organizzare la raccolta dei dati

1. Raccogli i tuoi dati. Se devi impararlo a scuola e fare un test, probabilmente otterrai un set di dati già pronto, come 1, 4, 5, 7, 10. Questo è il tuo set di dati o i numeri con cui lavorerai. Tuttavia, potresti dover organizzare tu stesso i numeri sulla base di una tabella o di una somma di storie. Assicurati che ogni numero si riferisca alla stessa cosa, ad esempio il numero di uova in ogni nido all`interno di un gruppo di uccelli, o il numero di parcheggi che ogni casa ha in una determinata strada.

2. Ordina il tuo set di dati in ordine crescente. Ciò significa che ordini i dati dal numero più basso a quello più alto. Dai un`occhiata ai seguenti esempi:

Esempio con un numero pari di numeri (set A): 4 7 9 11 12 20

Esempio con un numero dispari di numeri (set B): 5 8 10 10 15 18 23

3. Dividi i dati a metà. Per fare ciò, è necessario determinare il centro dei dati: il numero o i numeri che si trovano esattamente al centro del set di dati. Se hai un numero dispari di numeri, scegli il numero che si trova esattamente nel mezzo. Se hai un numero pari di numeri, il punto medio sarà tra i due numeri centrali.

Esempio con un numero pari di numeri (set A), in cui il punto medio è compreso tra 9 e 11: 4 7 9 | 11 12 20

Esempio con un numero dispari di numeri (insieme B), dove (10) è il centro: 5 8 10 (10) 15 18 23

Metodo 3 di 3: calcolo dell`intervallo interquartile

1. Determina la mediana della metà inferiore e superiore del tuo set di dati. La mediana è il "centro," o il numero nel mezzo di un set di dati. In questo caso non stai cercando il centro dell`intero set di dati, ma il centro relativo della metà superiore e inferiore. Se hai un numero dispari di numeri, non includere il loro punto medio. Ad esempio, nel set di dati B non dovresti includere una delle decine.

Esempio con un numero pari di numeri (set A):

Mediana della metà inferiore = 7 (Q1)
Mediana della metà superiore = 12 (Q3)

Esempio con un numero dispari di numeri (set B):

Mediana della metà inferiore = 8 (Q1)

Mediana della metà superiore = 18 (Q3)

2. Risolvi Q3 - Q1 per determinare l`intervallo interquartile. Ora sai quanti numeri sono compresi tra il 25° e il 75° percentile. Puoi usarlo per capire la dispersione dei dati. Ad esempio, se puoi ottenere un massimo di 100 punti su un test e l`intervallo interquartile dei voti ottenuti è 5, puoi presumere che la maggior parte delle persone che hanno sostenuto questo test conoscessero la stessa quantità dell`argomento. Non c`è molta differenza tra i numeri alti e bassi. Tuttavia, se l`intervallo interquartile dei voti ottenuti è 30, ci si potrebbe chiedere perché alcune persone hanno avuto un voto così alto e altri un voto così basso.

Esempio con un numero pari di numeri (set A): 12 - 7 = 5

Esempio con un numero dispari di numeri (set B): 18 - 8 = 10

Consigli

È importante imparare a calcolarlo da solo, ma ci sono diversi calcolatori online che puoi utilizzare per verificare di aver calcolato correttamente l`intervallo interquartile. Non fare troppo affidamento su un`app calcolatrice se devi impararlo per le lezioni di matematica a scuola. Se ti viene chiesto dell`intervallo interquartile su un test, dovrai essere in grado di calcolarlo a memoria.