Gli angoli retti sono spesso indicati nei libri di testo e nei test con un quadratino nell`angolo destro. Questa marcatura speciale significa "90 gradi." 
Se il tuo triangolo ha i lati di 3 e 4 e hai assegnato lettere a quei lati in modo che a = 3 e b = 4, risolvi l`equazione come: 3 + 4 = c. 
Se a = 3, a = 3 x 3 o 9.Se b = 4, allora b = 4 x 4 o 16. Quando consideri quei valori nella tua equazione, ora dovrebbe apparire così: 9 + 16 = c. 
Nel nostro esempio, 9 + 16 = 25, prendi nota allora 25 = c. 
Nel nostro esempio, c = 25.La radice quadrata di 25 è 5 (5 x 5 = 25, Così Sqrt(25) = 5).E questo significa c = 5, la lunghezza della nostra ipotenusa! 

Calcoli l`ipotenusa di questo triangolo in base alla lunghezza di una delle gambe e moltiplichi la sua lunghezza per Sqrt(2). È utile conoscere questo rapporto, soprattutto se i tuoi problemi di test o compiti a casa ti danno la lunghezza dei lati sotto forma di variabili anziché di numeri interi. 
Data la lunghezza della gamba più corta (quella opposta all`angolo di 30 gradi), moltiplica la lunghezza di quella gamba per 2 per ottenere la lunghezza dell`ipotenusa. Ad esempio, se la lunghezza della gamba più corta 4 è, allora sai che l`ipotenusa 8 deve essere. Se conosci la lunghezza della gamba più lunga (opposta all`angolo di 60 gradi), moltiplica quella lunghezza per2/Sqrt(3) per trovare la lunghezza dell`ipotenusa.Ad esempio, se la lunghezza della gamba più corta 4 è, allora sai che l`ipotenusa 4.62 deve essere. 

Per trovare il seno di un angolo di 80 gradi, lo farai peccato 80 deve digitare seguito dal segno di uguale o Invio, o80 peccato. (La risposta è -0,9939.) Puoi anche cercare "calcolatore del peccato" con il tuo browser per alcune calcolatrici facili da usare in modo da non dover indovinare. 
La regola del seno può infatti essere utilizzata per risolvere ogni triangolo, ma solo un triangolo rettangolo avrà un`ipotenusa. 

Ad esempio, se lo sai A = 40 gradi, poi B = 180 – (90 + 40). Semplifica questo a B = 180 – 130 e puoi dedurlo rapidamente B = 50 gradi. 
Per continuare con il nostro esempio, diciamo che la lunghezza del lato a = 10.Angolo C = 90 gradi, angolo A = 40 gradi e angolo B = 50 gradi. 

Partendo dal nostro esempio, lo vediamo peccato 40 = 0,64278761.Per trovare il valore di c, dividiamo la lunghezza di a per questo numero e troviamo quello 10 / 0,64278761 = 15,6, la lunghezza della nostra ipotenusa!
Determinazione della lunghezza dell'ipotenusa
Contenuto
Tutti i triangoli rettangoli hanno un angolo retto (di 90 gradi) e l`ipotenusa è il lato opposto a tale angolo. L`ipotenusa è il lato più lungo del triangolo ed è anche molto facile da trovare utilizzando diversi metodi. Questo articolo ti insegnerà come determinare la lunghezza dell`ipotenusa usando il teorema di Pitagora, a condizione che tu conosca la lunghezza degli altri due lati del triangolo. Quindi imparerai come calcolare l`ipotenusa di alcuni triangoli rettangoli speciali che incontrerai spesso nei test. E infine imparerai come calcolare la lunghezza dell`ipotenusa usando la regola del seno, quando si conosce solo la lunghezza di uno dei lati e la grandezza di uno degli angoli.
Passi
Metodo 1 di 3: utilizzo del teorema di Pitagora

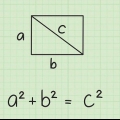
1. Impara il teorema di Pitagora. Il teorema di Pitagora descrive la relazione tra i lati di un triangolo rettangolo. Afferma che per un triangolo rettangolo arbitrario con lati aeb e ipotenusa di lunghezza c, abbiamo a + b = c.

2. Assicurati che il tuo triangolo sia un triangolo rettangolo.Il teorema di Pitagora funziona solo per i triangoli rettangoli e per definizione solo un triangolo rettangolo può avere un`ipotenusa.Se il tuo triangolo contiene un angolo esattamente di 90 gradi, allora è un triangolo rettangolo e puoi continuare.

3. Assegna le variabili a, b e c ai lati del triangolo.La variabile "C" è sempre assegnato all`ipotenusa, cioè il lato più lungo.Scegli uno degli altri lati per il un, e nominare il lato rimanente B (non importa quale, la matematica rimane la stessa).Quindi elaborare le lunghezze di aeb nella formula, come mostrato nell`esempio seguente:

4. Determina i quadrati di a e b.Per trovare il quadrato di un numero, basta moltiplicare quel numero per se stesso, quindi a = a x a. Trova i quadrati di aeb e incorporali nella formula.

5. Conta i valori diun e B insieme su. Scomponi questo nella tua equazione e ti dà il valore di c. Ora manca solo un passo e hai determinato l`ipotenusa!

6. Determina la radice quadrata di c. Usa la funzione radice quadrata sulla tua calcolatrice (o tabelline, se le conosci a memoria) per trovare la radice quadrata di c. La risposta è la lunghezza della tua ipotenusa!
Metodo 2 di 3: Determinazione dell`ipotenusa di triangoli rettangoli speciali

1. Impara a riconoscere i triangoli di un triangolo pitagorico. Le lunghezze dei lati di una triade di Pitagora sono interi che obbediscono al Teorema di Pitagora. Incontrerai regolarmente questi triangoli speciali nei libri di testo di geometria e nei test standard come il SAT e il GRE.In particolare, se memorizzi le prime 2 triple pitagoriche, puoi risparmiare molto tempo su quei test perché conosci immediatamente l`ipotenusa di uno qualsiasi di questi triangoli solo guardando le lunghezze dei lati!
- Il primo trio pitagorico lo è 3-4-5 (3 + 4 = 5, 9 + 16 = 25).Quando vedi un triangolo rettangolo con i lati di lunghezza 3 e 4, sai subito con certezza che l`ipotenusa sarà 5 senza dover fare alcun calcolo.
- Il rapporto di una terna pitagorica rimane lo stesso anche quando i lati vengono moltiplicati per un numero diverso. Ad esempio: un triangolo rettangolo con i lati 6 e 8 avrà un`ipotenusa di 10 (6 + 8 = 10, 36 + 64 = 100).Lo stesso vale per9-12-15, Anche 1.5-2-2.5.Fai i calcoli e vedrai!
- Il secondo trio pitagorico che incontrerai spesso nei test è 5-12-13 (5 + 12 = 13, 25 + 144 = 169).Fai attenzione anche ai suoi plurali, come 24-10-26 e 2.5-6-6.5.

2. Impara il rapporto tra i lati di un triangolo rettangolo con angoli 45-45-90. Un triangolo rettangolo 45-45-90 ha angoli di 45, 45 e 90 gradi ed è anche chiamato triangolo rettangolo isoscele. Questo si trova spesso nei test standard ed è un triangolo molto facile da risolvere. Il rapporto tra i lati di questo triangolo è 1:1:Sqrt(2), il che significa che la lunghezza delle gambe è uguale e la lunghezza dell`ipotenusa è quindi semplicemente la lunghezza delle gambe moltiplicata per la radice quadrata di due.

3. Impara le proporzioni di un triangolo 30-60-90 ad angolo retto. Questo triangolo ha angoli di 30, 60 e 90 gradi e può essere formato dividendo a metà un triangolo equilatero. I lati del triangolo rettangolo 30-60-90 hanno sempre il rapporto 1:Sqrt(3):2, o x:Sqrt(3)x:2x.Se data la lunghezza di una gamba del triangolo destro 30-60-90 e si chiede di determinare l`ipotenusa, è molto facile fare:
Metodo 3 di 3: Calcolo dell`ipotenusa con la regola del seno

1. Capisci cos`è "Seno" si intende. I termini "seno," "coseno" e "tangente" tutti si riferiscono a determinate relazioni tra gli angoli e/o i lati di un triangolo rettangolo.In un triangolo rettangolo, l`è seno di un angolo definito come la lunghezza del lato opposto all`angolo diviso per l`ipotenusa del triangolo. L`abbreviazione di seno come appare sulla calcolatrice è peccato.

2. Impara a calcolare il seno. Anche una semplice calcolatrice scientifica ha una funzione seno. Guarda la chiave contrassegnata peccato.Per trovare il seno di un angolo di solito premi il tasto peccato-quindi digitare l`angolo in gradi.Tuttavia, su alcune calcolatrici devi prima inserire l`angolo in gradi e poi premere il tasto peccato-premi il bottone. Dovrai sperimentare con la tua calcolatrice o guardare nel manuale per determinare quale è.

3. Impara la regola del seno.La regola del seno è uno strumento utile per risolvere i problemi del triangolo. Puoi usarlo principalmente per trovare l`ipotenusa di un triangolo rettangolo, se conosci la lunghezza di un lato e uno dei suoi angoli diversi dall`angolo retto. Per qualsiasi triangolo con i lati un, B e C e gli angoli un, B e C, la regola del seno lo afferma un / peccato un = B / peccato B = C / peccato C.

4. Assegna le variabili a, b e c ai lati del triangolo. L`ipotenusa (il lato più lungo) dovrebbe essere sempre la "C" sono. Per semplicità, etichetta il lato di lunghezza nota come "un" e altri "B". Quindi assegna le variabili A, B e C agli angoli del triangolo. Quindi diventa l`angolo retto opposto all`ipotenusa "C".L`angolo opposto "un" è l`angolo "un" e l`angolo opposto "B" è "B".

5. Calcola il terzo angolo. Perché è un angolo retto lo sai già C = 90 gradi e sai anche quale angolo un o B è. Poiché la somma di tutti gli angoli in un triangolo deve sempre essere uguale a 180 gradi, è facile calcolare il terzo angolo usando la formula: 180 – (90 + LA) = B. Puoi anche invertire questa equazione in modo che 180 – (90 + B) = A.

6. Esamina il tuo triangolo.A questo punto conosci tutti gli angoli del triangolo e la lunghezza del lato a. Ora è il momento di elaborare questi valori nella regola del seno, per calcolare la lunghezza degli altri due lati.

7. Applica la regola del seno al tuo triangolo.Dobbiamo solo elaborare i nostri numeri e risolvere la seguente equazione, per trovare la lunghezza dell`ipotenusa c: lunghezza lato a / peccato A = lunghezza lato c / peccato C.Questo può ancora sembrare un po` intimidatorio, ma il seno di 90 gradi è una costante ed è sempre uguale a 1!La nostra equazione può quindi essere semplificata in: un / peccato A = c / 1, o più semplice un / peccato A = c.

8. Dividi la lunghezza della setaun attraverso il seno dell`angolo un per trovare la lunghezza dell`ipotenusa!Puoi calcolarlo in due passaggi separati, dapprima: peccato Calcola e scrivi A, poi dividi per a. Oppure provalo tutto in una volta nella calcolatrice. Se lo fai, non dimenticare le parentesi dopo il segno di divisione.Ad esempio, digita 10 / (peccato 40) o 10 / (40 peccato), a seconda della calcolatrice.
Articoli sull'argomento "Determinazione della lunghezza dell'ipotenusa"
Condividi sui social network:
Simile
Popolare