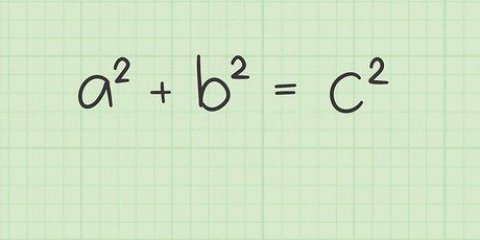Ad esempio, se la larghezza di un rettangolo è 3 cm e la lunghezza è 4 cm, la tua formula sarà simile a questa:  .
. 
Ad esempio:




Ad esempio:



Quindi, la diagonale o rettangolo con una larghezza di 3 cm e una lunghezza di 4 cm è di 5 cm. 

Ad esempio, se l`area del rettangolo è di 35 centimetri quadrati, la tua formula sarebbe simile a questa:  .
. 
Ad esempio:

 .
. 

Ad esempio, se il perimetro di un rettangolo è di 24 centimetri, la tua formula sarebbe simile a questa:  .
. 
Ad esempio:


 .
. 
Ad esempio, se hai trovato con la formula dell`area che  , quindi sostituisci il valore
, quindi sostituisci il valore  nella formula della circonferenza:
nella formula della circonferenza:



Ad esempio:




Ad esempio:




Ad esempio,  sta diventando
sta diventando  .
. 
Ad esempio, l`equazione  può essere sciolto
può essere sciolto  .
. 
Ad esempio:


E

 .
.
Quindi, la lunghezza e la larghezza del rettangolo sono 7 cm e 5 cm. 
Stai usando il teorema di Pitagora perché la diagonale di un rettangolo lo divide in due triangoli rettangoli congruenti. La larghezza e la lunghezza del rettangolo sono le lunghezze dei lati del triangolo; la diagonale è l`ipotenusa del triangolo. 
Ad esempio, se sai che la larghezza e la lunghezza del rettangolo sono 5 cm e 7 cm, la tua formula sarebbe simile a questa:  .
. 
Ad esempio:




Ad esempio:



Quindi la diagonale di un rettangolo con area di 35 cm e perimetro di 24 cm è di circa 8,6 cm. 

Puoi usare questo metodo se conosci il perimetro del rettangolo, tranne per il fatto che ora stai usando la formula del perimetro invece della formula dell`area. La formula per il perimetro di un rettangolo è  , per cui
, per cui  è uguale alla larghezza del rettangolo, e
è uguale alla larghezza del rettangolo, e  è uguale alla lunghezza del rettangolo.
è uguale alla lunghezza del rettangolo. 
Ad esempio, se l`area del rettangolo è di 35 centimetri quadrati, la tua formula assomiglierebbe a volt:  .
. 
Ad esempio, se l`hai trovato  , quindi sostituisci questa relazione con
, quindi sostituisci questa relazione con  nella formula dell`area:
nella formula dell`area:



Ad esempio:




Ad esempio, l`equazione  può essere sciolto come
può essere sciolto come  .
. 
Ad esempio:


E

 .
.
In questo caso c`è una risposta negativa. Poiché la lunghezza di un rettangolo non può essere negativa, sai che la lunghezza deve essere 5 cm. 
Ad esempio, se sai che la lunghezza del rettangolo è 5 cm e che il rapporto tra le lunghezze dei lati è  , quindi inserisci 5 come lunghezza nella formula:
, quindi inserisci 5 come lunghezza nella formula:




Usi il teorema di Pitagora perché la diagonale di un rettangolo lo divide in due triangoli rettangoli congruenti. La larghezza e la lunghezza del rettangolo sono le lunghezze dei lati del triangolo; la diagonale è l`ipotenusa del triangolo. 
Ad esempio, se sai che la larghezza e la lunghezza del rettangolo sono pari a 5 cm e 7 cm, la tua formula ora è simile a questa:  .
. 
Ad esempio:




Ad esempio:



Quindi la diagonale di un rettangolo con una larghezza che è 2 cm in più rispetto alla sua lunghezza, e ha un`area di 35 cm, è di circa 8,6 cm.
Calcola la lunghezza della diagonale in un rettangolo
Contenuto
Una diagonale è una linea retta che collega un angolo di un rettangolo con l`angolo opposto. Un rettangolo ha due diagonali, ciascuna della stessa lunghezza. Se conosci le lunghezze dei lati di un rettangolo, è facile trovare la lunghezza della diagonale usando il teorema di Pitagora, perché una diagonale divide un rettangolo in due triangoli rettangoli. Se non conosci le lunghezze dei lati, ma hai altri dati (come l`area e il perimetro, o il rapporto tra le lunghezze dei lati), puoi misurare la lunghezza e la larghezza dei lati con un qualche passaggio in più, trova il rettangolo e poi, usando il teorema di Pitagora, trova la lunghezza e la larghezza della diagonale.
Passi
Metodo 1 di 3: utilizzare la lunghezza e la larghezza

1. Scrivi la formula per il teorema di Pitagora. La formula è  , per cui
, per cui  e
e  sono uguali alle lunghezze dei lati di un triangolo rettangolo, e
sono uguali alle lunghezze dei lati di un triangolo rettangolo, e  è uguale alla lunghezza dell`ipotenusa di un triangolo rettangolo.
è uguale alla lunghezza dell`ipotenusa di un triangolo rettangolo.
 , per cui
, per cui  e
e  sono uguali alle lunghezze dei lati di un triangolo rettangolo, e
sono uguali alle lunghezze dei lati di un triangolo rettangolo, e  è uguale alla lunghezza dell`ipotenusa di un triangolo rettangolo.
è uguale alla lunghezza dell`ipotenusa di un triangolo rettangolo. - Usi il teorema di Pitagora perché la diagonale di un rettangolo lo divide in due triangoli rettangoli congruenti. La lunghezza e la larghezza del rettangolo sono le lunghezze dei lati del triangolo; la diagonale è l`ipotenusa del triangolo.

2. Applicare la lunghezza e la larghezza alla formula. Questi sono se è dato correttamente, oppure puoi misurarli. Assicurati di sostituire  e
e  .
.
 e
e  .
. .
.
3. Al quadrato la lunghezza e la larghezza, quindi somma questi numeri insieme. La quadratura sta moltiplicando il numero per se stesso.




4. Sottrarre la radice quadrata di ciascun lato dell`equazione. Il modo più semplice per trovare una radice quadrata è usare una calcolatrice. Puoi usare una calcolatrice online se non hai una calcolatrice scientifica. Questo ti dà il valore  , oppure l`ipotenusa del triangolo e la diagonale del rettangolo.
, oppure l`ipotenusa del triangolo e la diagonale del rettangolo.
 , oppure l`ipotenusa del triangolo e la diagonale del rettangolo.
, oppure l`ipotenusa del triangolo e la diagonale del rettangolo.


Quindi, la diagonale o rettangolo con una larghezza di 3 cm e una lunghezza di 4 cm è di 5 cm.
Metodo 2 di 3: Utilizzo dell`area e del perimetro

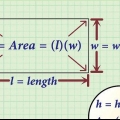
1. Scrivi la formula per l`area di un rettangolo. La formula è  , per cui
, per cui  è uguale all`area del rettangolo,
è uguale all`area del rettangolo,  è uguale alla lunghezza del rettangolo, e
è uguale alla lunghezza del rettangolo, e  è uguale alla larghezza del rettangolo.
è uguale alla larghezza del rettangolo.
 , per cui
, per cui  è uguale all`area del rettangolo,
è uguale all`area del rettangolo,  è uguale alla lunghezza del rettangolo, e
è uguale alla lunghezza del rettangolo, e  è uguale alla larghezza del rettangolo.
è uguale alla larghezza del rettangolo.
2. Usa l`area del rettangolo nella formula. Assicurati di sostituire la variabile corretta  .
.
 .
. .
.
3. Riorganizza la formula e ottieni un valore per w  . Puoi farlo dividendo entrambi i lati dell`equazione per
. Puoi farlo dividendo entrambi i lati dell`equazione per  . Metti da parte questo valore. Lo userai più avanti nella formula per il perimetro.
. Metti da parte questo valore. Lo userai più avanti nella formula per il perimetro.
 . Puoi farlo dividendo entrambi i lati dell`equazione per
. Puoi farlo dividendo entrambi i lati dell`equazione per  . Metti da parte questo valore. Lo userai più avanti nella formula per il perimetro.
. Metti da parte questo valore. Lo userai più avanti nella formula per il perimetro.
 .
.
4. Scrivi la formula per il perimetro di un rettangolo. La formula è  , per cui
, per cui  è uguale alla larghezza del rettangolo, e
è uguale alla larghezza del rettangolo, e  è uguale alla lunghezza del rettangolo.
è uguale alla lunghezza del rettangolo.
 , per cui
, per cui  è uguale alla larghezza del rettangolo, e
è uguale alla larghezza del rettangolo, e  è uguale alla lunghezza del rettangolo.
è uguale alla lunghezza del rettangolo.
5. Usa il valore del perimetro nella formula. Assicurati di sostituire la variabile  .
.
 .
. .
.
6. Dividi entrambi i membri dell`equazione per 2. Questo ti dà il valore  .
.
 .
.

 .
.
7. Usa il valore w  nell`equazione. Usa il valore che hai trovato riorganizzando la formula dell`area.
nell`equazione. Usa il valore che hai trovato riorganizzando la formula dell`area.
 nell`equazione. Usa il valore che hai trovato riorganizzando la formula dell`area.
nell`equazione. Usa il valore che hai trovato riorganizzando la formula dell`area. , quindi sostituisci il valore
, quindi sostituisci il valore  nella formula della circonferenza:
nella formula della circonferenza:


8. Elimina la frazione nell`equazione. Puoi farlo moltiplicando entrambi i lati dell`equazione per  .
.
 .
.



9. Imposta l`equazione uguale a 0. Puoi farlo sottraendo il termine di primo grado da entrambi i lati dell`equazione.




10. Riordina l`ordine dei termini nell`equazione. Ciò significa che viene prima il termine con l`esponente, seguito dal termine con la variabile e infine la costante. Durante la riorganizzazione, prestare attenzione ai segni positivi e negativi corretti. L`equazione è ora ordinata come equazione quadratica.
 sta diventando
sta diventando  .
.
11. Fattorizzare l`equazione quadratica. Per istruzioni dettagliate su come farlo, leggi l`articolo Risolvi equazioni quadratiche.
 può essere sciolto
può essere sciolto  .
.
12. Determina i valori di l  . Puoi farlo impostando ogni termine su zero e risolvendo la variabile. Ottieni due soluzioni a questa equazione. Poiché hai a che fare con un rettangolo, le due soluzioni saranno la larghezza e la lunghezza del tuo rettangolo.
. Puoi farlo impostando ogni termine su zero e risolvendo la variabile. Ottieni due soluzioni a questa equazione. Poiché hai a che fare con un rettangolo, le due soluzioni saranno la larghezza e la lunghezza del tuo rettangolo.
 . Puoi farlo impostando ogni termine su zero e risolvendo la variabile. Ottieni due soluzioni a questa equazione. Poiché hai a che fare con un rettangolo, le due soluzioni saranno la larghezza e la lunghezza del tuo rettangolo.
. Puoi farlo impostando ogni termine su zero e risolvendo la variabile. Ottieni due soluzioni a questa equazione. Poiché hai a che fare con un rettangolo, le due soluzioni saranno la larghezza e la lunghezza del tuo rettangolo.

E

 .
.Quindi, la lunghezza e la larghezza del rettangolo sono 7 cm e 5 cm.

13. Scrivi la formula per il teorema di Pitagora. La formula è  , per cui
, per cui  e
e  sono uguali alle lunghezze dei lati di un triangolo rettangolo, e
sono uguali alle lunghezze dei lati di un triangolo rettangolo, e  è uguale alla lunghezza dell`ipotenusa di un triangolo rettangolo.
è uguale alla lunghezza dell`ipotenusa di un triangolo rettangolo.
 , per cui
, per cui  e
e  sono uguali alle lunghezze dei lati di un triangolo rettangolo, e
sono uguali alle lunghezze dei lati di un triangolo rettangolo, e  è uguale alla lunghezza dell`ipotenusa di un triangolo rettangolo.
è uguale alla lunghezza dell`ipotenusa di un triangolo rettangolo.
14. Usa la latitudine e la longitudine nella formula. Non importa quale valore usi per quale variabile.
 .
.
15. Al quadrato la latitudine e la longitudine, quindi somma questi numeri insieme. Quadrare significa moltiplicare un numero per se stesso.




16. Prendi la radice quadrata di ciascun lato dell`equazione. Il modo più semplice per trovare una radice quadrata è usare una calcolatrice. Puoi usare una calcolatrice online se non hai una calcolatrice scientifica. Questo ti dà il valore  , e questa è l`ipotenusa del triangolo e la diagonale del rettangolo.
, e questa è l`ipotenusa del triangolo e la diagonale del rettangolo.
 , e questa è l`ipotenusa del triangolo e la diagonale del rettangolo.
, e questa è l`ipotenusa del triangolo e la diagonale del rettangolo.


Quindi la diagonale di un rettangolo con area di 35 cm e perimetro di 24 cm è di circa 8,6 cm.
Metodo 3 di 3: Utilizzo dell`area e delle lunghezze relazionali dei lati

1. Scrivi una formula che spieghi la relazione tra le lunghezze dei lati. È possibile modificare la lunghezza ( ) o la larghezza (
) o la larghezza ( ) isolato. Metti da parte questa formula per un momento. Presto lo utilizzerai nella formula della superficie.
) isolato. Metti da parte questa formula per un momento. Presto lo utilizzerai nella formula della superficie.
 ) o la larghezza (
) o la larghezza ( ) isolato. Metti da parte questa formula per un momento. Presto lo utilizzerai nella formula della superficie.
) isolato. Metti da parte questa formula per un momento. Presto lo utilizzerai nella formula della superficie. - Ad esempio, se sai che la larghezza di un rettangolo è 2 cm in più rispetto alla sua lunghezza, puoi scrivere una formula come
:
.

2. Scrivi la formula per l`area di un rettangolo. La formula è  , per cui
, per cui  è uguale all`area del rettangolo,
è uguale all`area del rettangolo,  è uguale alla lunghezza del rettangolo, e
è uguale alla lunghezza del rettangolo, e  è uguale alla larghezza del rettangolo.
è uguale alla larghezza del rettangolo.
 , per cui
, per cui  è uguale all`area del rettangolo,
è uguale all`area del rettangolo,  è uguale alla lunghezza del rettangolo, e
è uguale alla lunghezza del rettangolo, e  è uguale alla larghezza del rettangolo.
è uguale alla larghezza del rettangolo. , per cui
, per cui  è uguale alla larghezza del rettangolo, e
è uguale alla larghezza del rettangolo, e  è uguale alla lunghezza del rettangolo.
è uguale alla lunghezza del rettangolo.
3. Usa l`area del rettangolo nella formula. Assicurati di sostituire la variabile  .
.
 .
. .
.
4. Utilizzare la formula relazionale per la lunghezza (o larghezza) nella formula. Dal momento che hai a che fare con un rettangolo, non importa se stai lavorando con una variabile  o
o  .
.
 o
o  .
. , quindi sostituisci questa relazione con
, quindi sostituisci questa relazione con  nella formula dell`area:
nella formula dell`area:


5. Rendila un`equazione quadratica. Lo fai usando la proprietà distributiva e moltiplicando insieme i termini tra parentesi, dopodiché imposti l`equazione uguale a 0.




6. Fattorizzare l`equazione quadratica. Per istruzioni dettagliate su come farlo, leggi l`articolo Risolvi equazioni quadratiche.
 può essere sciolto come
può essere sciolto come  .
.
7. Determina i valori di l  . Lo fai rendendo ogni termine uguale a zero e risolvendo la variabile. Trovi due soluzioni all`equazione.
. Lo fai rendendo ogni termine uguale a zero e risolvendo la variabile. Trovi due soluzioni all`equazione.
 . Lo fai rendendo ogni termine uguale a zero e risolvendo la variabile. Trovi due soluzioni all`equazione.
. Lo fai rendendo ogni termine uguale a zero e risolvendo la variabile. Trovi due soluzioni all`equazione.

E

 .
.In questo caso c`è una risposta negativa. Poiché la lunghezza di un rettangolo non può essere negativa, sai che la lunghezza deve essere 5 cm.

8. Usa il valore della lunghezza (o larghezza) nella formula della relazione. Questo ti darà la lunghezza dell`altro lato del rettangolo.
 , quindi inserisci 5 come lunghezza nella formula:
, quindi inserisci 5 come lunghezza nella formula:



9. Scrivi la formula per il teorema di Pitagora. La formula è  , per cui
, per cui  e
e  sono uguali alle lunghezze dei lati di un triangolo rettangolo, e
sono uguali alle lunghezze dei lati di un triangolo rettangolo, e  è uguale alla lunghezza dell`ipotenusa di un triangolo rettangolo.
è uguale alla lunghezza dell`ipotenusa di un triangolo rettangolo.
 , per cui
, per cui  e
e  sono uguali alle lunghezze dei lati di un triangolo rettangolo, e
sono uguali alle lunghezze dei lati di un triangolo rettangolo, e  è uguale alla lunghezza dell`ipotenusa di un triangolo rettangolo.
è uguale alla lunghezza dell`ipotenusa di un triangolo rettangolo.
10. Usa la latitudine e la longitudine nella formula. Non importa quale valore usi per quale variabile.
 .
.
11. Al quadrato la latitudine e la longitudine, quindi somma questi numeri insieme. Quadrare significa moltiplicare un numero per se stesso.




12. Sottrarre la radice quadrata di ciascun lato dell`equazione. Il modo più semplice per trovare una radice quadrata è usare una calcolatrice. Puoi usare una calcolatrice online se non hai una calcolatrice scientifica. Questo ti dà il valore  , oppure l`ipotenusa del triangolo e quindi la diagonale del rettangolo.
, oppure l`ipotenusa del triangolo e quindi la diagonale del rettangolo.
 , oppure l`ipotenusa del triangolo e quindi la diagonale del rettangolo.
, oppure l`ipotenusa del triangolo e quindi la diagonale del rettangolo.


Quindi la diagonale di un rettangolo con una larghezza che è 2 cm in più rispetto alla sua lunghezza, e ha un`area di 35 cm, è di circa 8,6 cm.
Articoli sull'argomento "Calcola la lunghezza della diagonale in un rettangolo"
Condividi sui social network:
Simile
Popolare