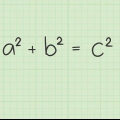Ad esempio, se vuoi trovare la larghezza di un rettangolo con un`area di 24 cm e una lunghezza di 8 cm, la tua formula sarebbe simile a questa:


Ad esempio, nell`equazione  , dividere ogni lato per 8.
, dividere ogni lato per 8.




Ad esempio, per un rettangolo con un`area di  e una lunghezza di
e una lunghezza di  , diventa la larghezza
, diventa la larghezza  .
. 
Ad esempio, se volessi trovare la larghezza di un rettangolo con una circonferenza di 22 cm e una lunghezza di 8 cm, la formula sarebbe simile a questa:



Ad esempio, nell`equazione  , sottrarre 16 da ciascun lato e dividere per 2.
, sottrarre 16 da ciascun lato e dividere per 2.





Ad esempio, per un rettangolo con un perimetro di  e una lunghezza di
e una lunghezza di  , diventa la larghezza
, diventa la larghezza  .
. 

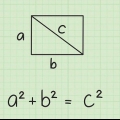
Ad esempio, quando si determina la larghezza di un rettangolo con una diagonale di 5 cm e un lato di 4 cm, la formula sarebbe simile a questa: 

Ad esempio:




Ad esempio, nell`equazione  , sottrarre 16 da ciascun lato.
, sottrarre 16 da ciascun lato.



Ad esempio:



Ad esempio, per un rettangolo con una diagonale di  e un lato di
e un lato di  , diventa la larghezza
, diventa la larghezza  .
. 

La relazione può essere data affermando quante volte un lato è maggiore dell`altro, o quante unità in più o in meno. Ad esempio, si può sapere che la lunghezza è cinque centimetri più lunga della larghezza. L`espressione per la lunghezza diventa quindi  .
. 
Ad esempio, se sai che l`area è di 24 cm e quello  , allora la formula si presenta così:
, allora la formula si presenta così:



Ad esempio, semplificare  Fino a
Fino a  .
. 
Potrebbe essere necessario aggiungere o sottrarre per risolverlo, o fattorizzare o utilizzare un`equazione quadratica per risolverlo. Ad esempio,  può essere sciolto come segue:
può essere sciolto come segue:


Quindi hai due possibili soluzioni per :
: o
o  . Poiché un rettangolo non può avere una larghezza negativa, puoi escludere -8. Così è la tua soluzione
. Poiché un rettangolo non può avere una larghezza negativa, puoi escludere -8. Così è la tua soluzione  .
.
Determinazione della larghezza di un rettangolo
Contenuto
Esistono numerosi modi per trovare le dimensioni mancanti di un rettangolo e il metodo che utilizzerai dipenderà dai dati che hai. Se si conosce l`area o il perimetro, così come la lunghezza di un lato del rettangolo (o il rapporto tra la sua lunghezza e la sua larghezza), è possibile determinare la dimensione mancante. Le proprietà di un rettangolo sono tali che questi metodi possono essere utilizzati per determinarne la latitudine o la longitudine.
Passi
Metodo 1 di 4: Utilizzo dell`area e della lunghezza

1. Annota la formula per l`area di un rettangolo. La formula è  , per cui
, per cui  è uguale all`area del rettangolo,
è uguale all`area del rettangolo,  è uguale alla lunghezza del rettangolo, e
è uguale alla lunghezza del rettangolo, e  è uguale alla larghezza del rettangolo.
è uguale alla larghezza del rettangolo.
 , per cui
, per cui  è uguale all`area del rettangolo,
è uguale all`area del rettangolo,  è uguale alla lunghezza del rettangolo, e
è uguale alla lunghezza del rettangolo, e  è uguale alla larghezza del rettangolo.
è uguale alla larghezza del rettangolo. - Il metodo funziona solo per una determinata area e lunghezza del rettangolo.
- Questa formula è disponibile anche nel modulo
, per cui
è uguale all`altezza del rettangolo (anziché alla lunghezza). Questi due termini si riferiscono alle stesse dimensioni.

2. Usa i valori di area e lunghezza nella formula. Assicurati di sostituire le variabili corrette.


3. Risolvere per w  . Puoi farlo dividendo ciascun lato dell`equazione per la sua lunghezza.
. Puoi farlo dividendo ciascun lato dell`equazione per la sua lunghezza.
 . Puoi farlo dividendo ciascun lato dell`equazione per la sua lunghezza.
. Puoi farlo dividendo ciascun lato dell`equazione per la sua lunghezza. , dividere ogni lato per 8.
, dividere ogni lato per 8.



4. Scrivi la tua risposta finale. Non dimenticare di menzionare l`unità di lettura.
 e una lunghezza di
e una lunghezza di  , diventa la larghezza
, diventa la larghezza  .
.Metodo 2 di 4: Utilizzo della circonferenza e della lunghezza
1. Scrivi la formula per il perimetro di un rettangolo. La formula è  , per cui
, per cui  è uguale al perimetro del rettangolo,
è uguale al perimetro del rettangolo,  è uguale alla lunghezza del rettangolo, e
è uguale alla lunghezza del rettangolo, e  è uguale alla larghezza del rettangolo.
è uguale alla larghezza del rettangolo.
 , per cui
, per cui  è uguale al perimetro del rettangolo,
è uguale al perimetro del rettangolo,  è uguale alla lunghezza del rettangolo, e
è uguale alla lunghezza del rettangolo, e  è uguale alla larghezza del rettangolo.
è uguale alla larghezza del rettangolo.- Questo metodo funziona solo per un determinato perimetro e lunghezza del rettangolo.
- Questa formula è anche scritta come
, per cui
è uguale all`altezza del rettangolo e viene utilizzata al posto della lunghezza. Le variabili
e
si riferiscono alle stesse dimensioni e la proprietà distributiva impone che queste due formule, sebbene ordinate in modo diverso, producano lo stesso risultato.

2. Usa la circonferenza e la lunghezza nella formula. Assicurati di sostituire le variabili corrette.



3. Risolvere w  . Per fare ciò, devi sottrarre la lunghezza da ciascun lato dell`equazione e dividerla per 2.
. Per fare ciò, devi sottrarre la lunghezza da ciascun lato dell`equazione e dividerla per 2.
 . Per fare ciò, devi sottrarre la lunghezza da ciascun lato dell`equazione e dividerla per 2.
. Per fare ciò, devi sottrarre la lunghezza da ciascun lato dell`equazione e dividerla per 2. , sottrarre 16 da ciascun lato e dividere per 2.
, sottrarre 16 da ciascun lato e dividere per 2.




4. Scrivi la risposta finale. Non dimenticare di menzionare l`unità di lettura.
 e una lunghezza di
e una lunghezza di  , diventa la larghezza
, diventa la larghezza  .
.Metodo 3 di 4: Usare la diagonale e la lunghezza

1. Scrivi la formula per la diagonale di un rettangolo. La formula è  , per cui
, per cui  è uguale alla lunghezza della diagonale,
è uguale alla lunghezza della diagonale,  è uguale alla lunghezza, e
è uguale alla lunghezza, e  è uguale alla larghezza del rettangolo.
è uguale alla larghezza del rettangolo.
 , per cui
, per cui  è uguale alla lunghezza della diagonale,
è uguale alla lunghezza della diagonale,  è uguale alla lunghezza, e
è uguale alla lunghezza, e  è uguale alla larghezza del rettangolo.
è uguale alla larghezza del rettangolo. - Questo metodo funziona solo per una determinata lunghezza della diagonale e per la lunghezza di un lato del rettangolo.
- Questa formula è anche scritta come
, per cui
è uguale all`altezza del rettangolo e viene utilizzata al posto della lunghezza. Le variabili
e
fare riferimento alle stesse letture.

2. Sostituisci i valori della diagonale e del lato nella formula. Assicurati di sostituire le variabili corrette.


3. Al quadrato entrambi i lati della formula. Devi farlo per sbarazzarti del segno radicale in modo che l`isolamento della variabile di larghezza diventi più facile.




4. Isola la variabile w  . Lo fai sottraendo la lunghezza al quadrato, da ciascun lato dell`equazione.
. Lo fai sottraendo la lunghezza al quadrato, da ciascun lato dell`equazione.
 . Lo fai sottraendo la lunghezza al quadrato, da ciascun lato dell`equazione.
. Lo fai sottraendo la lunghezza al quadrato, da ciascun lato dell`equazione. , sottrarre 16 da ciascun lato.
, sottrarre 16 da ciascun lato.


5. Risolvere per w  . Puoi farlo determinando la radice quadrata per ciascun lato dell`equazione.
. Puoi farlo determinando la radice quadrata per ciascun lato dell`equazione.
 . Puoi farlo determinando la radice quadrata per ciascun lato dell`equazione.
. Puoi farlo determinando la radice quadrata per ciascun lato dell`equazione.


6. Scrivi la risposta finale. Non dimenticare di menzionare l`unità di lettura.
 e un lato di
e un lato di  , diventa la larghezza
, diventa la larghezza  .
.Metodo 4 di 4: Utilizzo dell`area o del perimetro e della lunghezza relativa

1. Scrivi la formula per l`area o il perimetro di un rettangolo. La formula da utilizzare dipende dai valori misurati dati. Se viene fornita l`area, utilizzare la formula dell`area. Se viene data la circonferenza, utilizzare la formula della circonferenza.
- Se l`area o il perimetro sono sconosciuti o la relazione tra la lunghezza e la larghezza, non è possibile utilizzare questo metodo.
- La formula per l`area è
.
- La formula per la circonferenza è
.
- Ad esempio, forse dato che l`area di un rettangolo è 24 cm, allora usi la formula per l`area di un rettangolo.

2. Scrivi l`espressione che descrive la relazione tra la lunghezza e la larghezza. Scrivi la tua espressione in un confronto con  .
.
 .
. .
.
3. Sostituisci la variabile l  nella formula dell`area o del perimetro dall`espressione per la lunghezza. La formula ora sente solo la variabile
nella formula dell`area o del perimetro dall`espressione per la lunghezza. La formula ora sente solo la variabile  il che significa che puoi calcolare la larghezza.
il che significa che puoi calcolare la larghezza.
 nella formula dell`area o del perimetro dall`espressione per la lunghezza. La formula ora sente solo la variabile
nella formula dell`area o del perimetro dall`espressione per la lunghezza. La formula ora sente solo la variabile  il che significa che puoi calcolare la larghezza.
il che significa che puoi calcolare la larghezza. , allora la formula si presenta così:
, allora la formula si presenta così:


4. Semplifica l`equazione. L`equazione semplificata può assumere forme diverse, a seconda del rapporto tra la lunghezza e la larghezza, ea seconda che si tratti dell`area o del perimetro. Prova a fare un confronto con il quale tu  può risolvere il più facilmente possibile.
può risolvere il più facilmente possibile.
 può risolvere il più facilmente possibile.
può risolvere il più facilmente possibile. Fino a
Fino a  .
.
5. Risolvere per w  . Ancora una volta, come fai
. Ancora una volta, come fai  risolve dipende dall`equazione semplificata. Usa le regole di base dell`algebra e della geometria per risolvere questo problema.
risolve dipende dall`equazione semplificata. Usa le regole di base dell`algebra e della geometria per risolvere questo problema.
 . Ancora una volta, come fai
. Ancora una volta, come fai  risolve dipende dall`equazione semplificata. Usa le regole di base dell`algebra e della geometria per risolvere questo problema.
risolve dipende dall`equazione semplificata. Usa le regole di base dell`algebra e della geometria per risolvere questo problema. può essere sciolto come segue:
può essere sciolto come segue:

Quindi hai due possibili soluzioni per
 :
: o
o  . Poiché un rettangolo non può avere una larghezza negativa, puoi escludere -8. Così è la tua soluzione
. Poiché un rettangolo non può avere una larghezza negativa, puoi escludere -8. Così è la tua soluzione  .
.Articoli sull'argomento "Determinazione della larghezza di un rettangolo"
Condividi sui social network:
Simile
Popolare