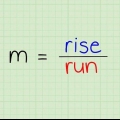Come Determinare l'Inclinazione di una Linea

Contenuto

Passi

La pendenza di una linea è una misura della velocità con cui la linea cambia. Questo può essere fatto con una linea retta -- dove la pendenza ti dice esattamente quanto in alto (pendenza positiva) o in discesa (pendenza negativa) una linea va su una certa distanza. La pendenza può essere utilizzata anche per una tangente a una curva. Oppure potrebbe essere una linea curva, utilizzata in analisi, in cui la pendenza è anche nota come "derivata" di una funzione. Ad ogni modo, basti pensare alla pendenza come al "tasso di variazione" di un grafico: se la variabile "x" diventa più grande, a quale velocità cambia "y"?? Questo è un modo di pensare alla pendenza come causa ed effetto.

Passi

Metodo 1 di 3: Trovare la pendenza di un`equazione lineare

Immagine titolata Find the Slope of an Equation Step 1

1. Usa la pendenza per determinare la pendenza e in quale direzione (su o giù) va una linea. Determinare la pendenza di una retta è facile, purché tu abbia o possa elaborare un`equazione lineare. Questo metodo funziona solo quando:

Le variabili non hanno esponenti.
Esistono solo due variabili e nessuna di esse è una frazione (ad esempio, le seguenti non possono essere: $\frac{1}{X}$ ${frac{1}{x}}$ )
L`equazione può essere semplificata nella forma $y = m X + B$ $y=mx+b$ , per cui m e B costanti (numeri come 3, 10, -12, $\frac{4}{3}, \frac{3}{5}$ ${frac{4}{3}},{frac{3}{5}}$ ).

2. Trova il numero prima della x, solitamente scritto come `m` per determinare la pendenza. Se l`equazione è già nella forma corretta,

y = m X + B

$y=mx+b$ , quindi scegli il numero nella posizione `m` (ma se non c`è un numero prima di x, la pendenza è 1). Quindi questa è anche la pendenza! Sappi che questo numero, m, è sempre moltiplicato per la variabile, in questo caso una `x`. Dai un`occhiata ai seguenti esempi:

y = 2 X + 6

$y=2x+6$

Pendenza = 2

y = 2 - X

$y=2-x$

Pendenza = -1

y = \frac{3}{8} X - 10

$y={frac{3}{8}}x-10$

pendenza = $\frac{3}{8}$ ${frac{3}{8}}$

Immagine titolata Find the Slope of an Equation Step 3

3. Riconoscere l`equazione in cui una variabile è isolata se la pendenza non è chiara. Puoi aggiungere, sottrarre, moltiplicare, ecc. per isolare una variabile (di solito la `y`). Ricorda che qualunque cosa tu faccia su un lato del segno di uguale (come aggiungere 3), devi farlo anche sull`altro lato. Il tuo obiettivo finale è un`equazione, tipo

y = m X + B

$y=mx+b$ . Ad esempio:

Trova la pendenza di $2 y - 3 = 8 X + 7$ $2y-3=8x+7$

Convertilo nel modulo $y = m X + B$ $y=mx+b$ :

2 y - 3 + 3 = 8 X + 7 + 3

$2y-3+3=8x+7+3$

2 y = 8 X + 10

$2y=8x+10$

2 y 2 = 8 X + 10 2

${frac{2y}{2}}={frac{8x+10}{2}}$

y = 4 X + 5

$y=4x+5$

Determina la pendenza:

Pendenza = M = 4

Metodo 2 di 3: Determinazione della pendenza con due punti

Immagine titolata Find the Slope of an Equation Step 4

1. Usa un grafico e due punti per trovare rapidamente la pendenza senza l`equazione. Se hai un grafico e una linea ma nessuna equazione, puoi comunque determinare la pendenza con facilità. Tutto ciò di cui hai bisogno sono due punti sulla linea, che applichi all`equazione

y 2 - y_{1} X 2 - X_{1}

${frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Quando determini la pendenza, tieni a mente le seguenti informazioni per assicurarti di essere sulla strada giusta:

Pendenze positive salgono e verso destra.
Pendenze negative scendono verso destra.
I pendii più ripidi sono linee più ripide. I pendii meno ripidi sono sempre più graduali.
Le linee orizzontali perfette hanno una pendenza pari a zero.
Le linee perfettamente verticali non hanno alcuna pendenza. La loro pendenza (o pendenza) è `indefinita`.

Immagine titolata Find the Slope of an Equation Step 5

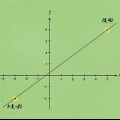
2. Scegli due punti, mettendoli nella forma semplice (x, y). Usa il grafico (o la domanda di assegnazione) per trovare le coordinate xey di due punti sul grafico. Possono essere costituiti da due punti qualsiasi attraverso cui passa la linea. Si supponga ad esempio che in questo metodo la retta passi per il punto (2.4) e per la (6.6).

In ogni coppia, la coordinata x è il primo numero e la coordinata y è il secondo numero dopo il punto decimale.

Ogni coordinata x su una linea ha una coordinata y corrispondente.

Immagine titolata Find the Slope of an Equation Step 6

3. Etichetta i punti x₁, y₁, X₂, y₂, e mantieni ogni punto con la sua coppia. Continuando con il nostro primo esempio, usando i punti (2.4) e (6.6), etichettare le coordinate xey di ciascun punto. Se tutto è andato bene, ora ti ritroverai con:

X₁: 2

y₁: 4

X₂: 6

y₂: 6

Immagine titolata Find the Slope of an Equation Step 7

4. Sostituisci questi punti nella "formula punto-pendenza" per trovare la pendenza. La seguente formula viene utilizzata per determinare la pendenza utilizzando due punti qualsiasi su una retta: $y 2 - y_{1} X 2 - X_{1}$ ${frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Basta sostituire i quattro punti e semplificare:

Punti originali: (2.4) e (6.6).

Applicare alla formula punto-pendenza:

6 - 4 6 - 2

${frac{6-4}{6-2}}$

Semplifica per la risposta finale:

$\frac{2}{4} = \frac{1}{2}$ ${frac{2}{4}}={frac{1}{2}}$ = pendenza

Immagine titolata Find the Slope of an Equation Step 8

5. Comprendere come funziona la formula punto-pendenza. La pendenza di una retta è indicata dalla variazione di y da x (y/x): quanto sale la retta diviso per quanto la retta continua a destra. L`aumento della linea è la differenza tra i valori y (ricorda, l`asse y va su e giù), e l`aumento della linea è la differenza tra i valori x (e l`asse x va da da sinistra a destra).

Immagine titolata Find the Slope of an Equation Step 9

6. Impara altri modi che devi conoscere per determinare la pendenza. L`equazione della pendenza è

y 2 - y_{1} X 2 - X_{1}

${frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Questo può anche essere rappresentato dalla lettera greca `Δ` (`delta`), che significa `differenza`. La pendenza può anche essere rappresentata come Δy/Δx, che significa `differenza di y` / `differenza di x`. Questa è esattamente la stessa domanda di "Determina la pendenza tra.."

Metodo 3 di 3: utilizzare il calcolo differenziale per trovare la pendenza di una curva

Immagine titolata Find the Slope of an Equation Step 10

1. Esamina come determinare la derivata di funzioni comuni in diversi modi. I derivati ti danno il tasso di variazione (o pendenza) in un punto di una linea. La linea può essere curva o dritta, non importa. Ricorda come cambia la linea in un dato momento, piuttosto che come cambia la pendenza dell`intera linea. Il modo in cui determini la derivata dipende dal tipo di funzione, quindi rivedi come determinare la derivata delle funzioni prima di continuare.

Leggi qui sulla determinazione della derivata
Le derivate più semplici, quelle per equazioni esponenziali standard, puoi trovare facilmente con un metodo rapido. Lo userai nel resto del metodo.

Immagine titolata Find the Slope of an Equation Step 11

2. Comprendere quali problemi richiedono di calcolare la pendenza utilizzando le derivate. Non ti verrà sempre richiesta esplicitamente la derivata o la pendenza di una curva. Potrebbe anche essere chiesto del "tasso di variazione" al punto (x, y). Potrebbe essere richiesta un`equazione per la pendenza del grafico, il che significa semplicemente trovare la derivata. Infine, ti potrebbe essere chiesto `la pendenza della retta tangente in (x, y)`. Ciò significa ancora una volta che richiede solo la pendenza della curva in un punto specifico (x, y).

Con questo metodo, poniti la seguente domanda: "Qual è la pendenza della linea

F (X) = 2 X 2 + 6 X

$f(x)=2x^{2}+6x$ al punto (4.2)?"

Il derivato è spesso scritto come

F^{sesso} (X), y^{sesso},

Immagine titolata Find the Slope of an Equation Step 12

3.Trova la derivata della funzione. Non hai nemmeno bisogno di un grafico reale, solo la funzione o l`equazione del grafico. In questo esempio utilizziamo una funzione discussa in precedenza,

4X+6 $F$

Immagine titolata Find the Slope of an Equation Step 13

4.Sostituisci il punto nell`equazione della derivata per trovare la pendenza. Il differenziale di una funzione ti dà la pendenza della funzione in un dato punto. In altre parole, f"(x) è la pendenza della funzione in qualsiasi momento (x,f(x)). Quindi per questo problema di esercizio: