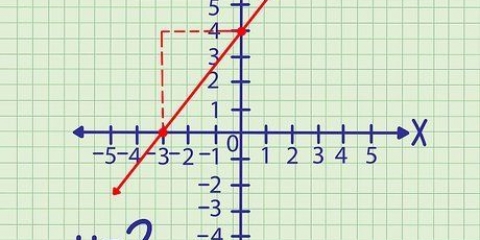
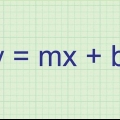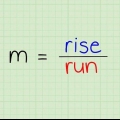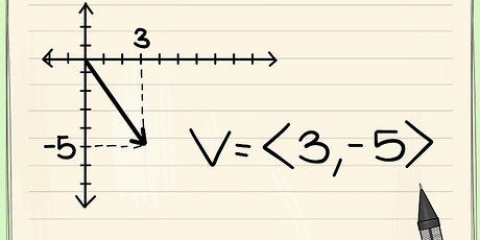(3-5)/(8-2) = -2/6 = -1/3 La pendenza della linea è -1/3. Per trovare questa pendenza, devi semplificare 2/6 ai suoi valori più piccoli, 1/3, poiché sia 2 che 6 sono divisibili per 2. 
Il reciproco negativo di -1/3 è 3 perché 3/1 è il reciproco di 1/3 e il segno è cambiato da negativo a positivo. 

3 --> y = mx + b = y = 3x + b 
(5, 4) --->y = 3x + b = 4 = 3(5) + b = 4 = 15 + b 
4 = 15 + b = -11 = b b = -11 
y = mx + b y = 3x - 11 L`equazione della bisettrice perpendicolare per i punti (2, 5) e (8, 3) è y = 3 x - 11.
Determinazione della bisettrice perpendicolare di due punti
Contenuto
Una bisettrice perpendicolare è una retta che divide in due un segmento collegato da due punti con un angolo di 90 gradi. Per trovare la bisettrice perpendicolare di due punti, tutto ciò che devi fare è trovare i loro punti medi e il reciproco, quindi applicare le risposte all`equazione di una retta della forma y = mx + b. Se vuoi sapere come trovare la bisettrice perpendicolare di due punti, segui i passaggi seguenti.
Passi
Metodo 1 di 2: raccogliere informazioni

1. Trova il centro dei due punti. Trova il punto medio di due punti applicando i punti alla formula del punto medio: [(X1 + X2)/2,( e1 + y2)/2]. Ciò significa che fai la media delle coordinate xey dei due punti, che ti dà il centro delle due coordinate. Supponiamo di lavorare con le coordinate (x1, y1) di (2, 5) e le coordinate (x2, y2) da (8, 3). Determinare il centro dei due punti come segue:
- [(2+8)/2, (5 +3)/2] =
- (2/10, 2/8) =
- (5, 4)
- Le coordinate del centro di (2, 5) e (8, 3) sono (5, 4).

2. Trova la pendenza dei due punti. Per trovare la pendenza (pendenza) dei due punti, applica i punti alla formula della pendenza: (s2 - y1) / (X2 - X1). La pendenza di una linea è la distanza di una variazione verticale sulla distanza di una corrispondente variazione orizzontale. Determinare la pendenza della retta attraverso i punti (2, 5) e (8, 3) come segue:

3. Trova il reciproco negativo della pendenza dei due punti. Per trovare il reciproco negativo di una pendenza, prendi il reciproco della pendenza e cambia il segno. Puoi trovare il reciproco di un numero invertendo le coordinate xey. Il reciproco negativo di 1/2 è -2/1, o solo -2; il reciproco di -4 è 1/4.
Metodo 2 di 2: Calcola l`equazione della retta

1. Scrivi l`equazione di una retta nella forma y = mx + b. L`equazione di una retta passante per due punti è della forma `y = mx + b ` dove le coordinate xey sulla linea sono rappresentate da `x` e `y`, la `m` rappresenta la pendenza della linea e la `b` rappresenta l`intersezione della linea con l`asse y. Dopo aver scritto questa equazione, puoi iniziare a trovare l`equazione della bisettrice perpendicolare dei due punti.

2. Applicare il reciproco negativo della pendenza originale all`equazione. Il reciproco negativo della pendenza dei punti (2, 5) e (8, 3) era 3. La `m` nell`equazione rappresenta la pendenza, quindi inserisci 3 per la `m` nell`equazione di una retta, y = mx + b.

3. Applicare il punto medio alla linea. Sai già che i punti medi dei punti (2, 5) e (8, 3) sono uguali a (5, 4). Poiché la bisettrice perpendicolare passa per i punti medi delle due rette, puoi applicare le coordinate dei punti medi all`equazione della retta. Basta compilare (5, 4) al posto delle coordinate xey della linea.

4. Risolvi per l`incrocio. Hai trovato tre delle quattro variabili nell`equazione della retta. Ora hai abbastanza informazioni per determinare la restante variabile `b`, l`intersezione di questa linea con l`asse y. Isolare la variabile `b` per determinarne il valore. Sottrai 15 da entrambi i membri dell`equazione.

5. Scrivi l`equazione della bisettrice perpendicolare. Per scrivere l`equazione della bisettrice perpendicolare, sostituire la pendenza della retta (3) e l`intersezione con l`asse y (-11) nell`equazione della forma y = mx + b. Non inserire nulla per le coordinate xey, perché con questa equazione puoi trovare qualsiasi coordinata sulla linea compilando una coordinata x o una y.
Articoli sull'argomento "Determinazione della bisettrice perpendicolare di due punti"
Condividi sui social network:
Simile
Popolare