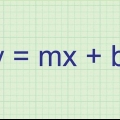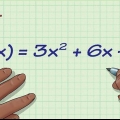La derivata di un esponente è l`esponente moltiplicato per la potenza -1 di un numero. Quindi, la derivata di x è 5x e la derivata di x è 3.5 volte. Se c`è già un numero davanti alla x, moltiplicalo per l`esponente. Ad esempio: la derivata di 3x è 12x. La derivata di qualsiasi costante è zero. Quindi la derivata di 8 è 0. La derivata di una somma è la somma di ogni singola derivata. Ad esempio: la derivata di x + 3x è 3x + 6x. La derivata di un prodotto è il primo fattore moltiplicato per la derivata del secondo fattore più il secondo fattore per la derivata del primo. Ad esempio , la derivata di x(2x + 1) è x(2) + (2x + 1)3x, che è uguale a 8x + 3x. La derivata di un quoziente (diciamo, f/g) è [g(derivata di f) - f(derivata di g)]/g. Ad esempio: la derivata di (x + 2x - 21)/(x - 3) è (x - 6x + 15)/(x - 3). 






Determinazione di una derivata
Contenuto
Le derivate possono essere utilizzate per determinare caratteristiche utili di un grafico, come massimi, minimi, picchi e valli e pendenze. Puoi persino usarli per disegnare equazioni complesse senza una calcolatrice grafica! Sfortunatamente, determinare la derivata di un`equazione è spesso un compito difficile, ma questo articolo ti aiuterà con una serie di suggerimenti e trucchi.
Passi

1. Comprendere la notazione di una derivata. I seguenti due modi di annotazione sono i più comuni, ma si possono trovare numerosi altri modi Wikipedia.
- Notazione Leibniz Questa notazione è più comunemente usata quando l`equazione contiene ay e x. Dy/dx significa letteralmente "la derivata di y rispetto a x". Prova a pensarlo come Δy/Δx per i valori di xey dove la differenza è infinitesima. Questa spiegazione dà naturalmente la definizione di un limite rispetto alla derivata: limh->0 (f(x+h)-f(x))/h. Applicando questa notazione alla derivata seconda, scrivi: dy/dx.
- Notazione di Lagrange La derivata di una funzione f si scrive anche come f`(x). Questa notazione è pronunciata come "la funzione f di x". Questa notazione è più breve di quella di Leibniz e viene utilizzata quando si considera una derivata come una funzione. Per le derivate superiori basta aggiungerne un`altra " ` " pronta per "F", facendo sembrare la seconda derivata come f``(x).

2. Capire cos`è un derivato e a cosa serve. Innanzitutto, per trovare la pendenza di un grafico lineare, vengono presi due punti sulla linea e queste coordinate vengono inserite nell`equazione (y2 - y1)/(X2 - X1). Ma questo è possibile solo con i grafici lineari. Per le equazioni quadratiche e superiori, il grafico è una curva, quindi la differenza tra due punti non è sufficientemente precisa. Per trovare la pendenza di una tangente di una parabola, vengono presi due punti e riempiti nell`equazione, per determinare la pendenza di una linea curva: [f(x + dx) - f(x)]/dx. Dx significa"delta x," qual è la differenza tra le due coordinate x dei due punti del grafico. Si noti che questa equazione è la stessa di (y2 - y1)/(X2 - X1), ma in forma diversa. Poiché è già noto che il risultato non sarà accurato, viene scelta un`approssimazione indiretta. Per trovare la pendenza della tangente nel punto (x, f(x)), dx deve avvicinarsi a 0 in modo che i due punti scelti siano quasi uguali.Ma non puoi dividere per 0, quindi dopo aver riempito i valori dei due punti devi eliminare dedx al denominatore. Se questo ha successo, rendi dx uguale a 0 e risolvi. Questa è la pendenza della tangente in (x, f(x)). La derivata di un`equazione è l`equazione generale per trovare la pendenza di qualsiasi tangente di un grafico. Può sembrare molto difficile, ma gli esempi seguenti ti mostreranno come determinare la derivata.
Metodo 1 di 4: Differenziazione esplicita

1. Usa la differenziazione esplicita se y è già su un lato dell`equazione.

2. Sostituisci un`equazione in un`altra equazione [f(x + dx) - f(x)]/dx. Ad esempio, l`equazione y = x, la cui derivata è [(x + dx) - x]/dx.

3. Espandi ulteriormente dx per ottenere l`equazione [dx(2x + dx)]/dx. Ora è possibile eliminare la dx al numeratore e al denominatore. Il risultato è 2x + dx e quando dx si avvicina a 0 la derivata diventa 2x. Questa è la pendenza di qualsiasi tangente al grafico y = x è 2x. Inserisci semplicemente il valore di un dato punto x di cui vuoi trovare la tangente nell`equazione.

4. Impara a riconoscere gli schemi dello stesso tipo di equazioni. Di seguito ne troverai alcuni.
Metodo 2 di 4: Differenziazione implicita

1. Usa la differenziazione implicita quando la tua equazione non può essere scritta semplicemente con la y su un lato del segno di uguale. Anche se lo scrivi con la y su un lato, calcolare dy/dx sarebbe comunque un lavoro ingrato. Di seguito è riportato un esempio di come risolvere questo tipo di equazione.

2. In questo esempio, xy + 2y = 3x + 2y, sostituisci jey con f(x), in modo che sia chiaro che questa è effettivamente una funzione. L`equazione diventa quindi xf(x) + 2[f(x)] = 3x + 2f(x).

3. Per trovare la derivata di questa equazione, differenzia (una parola impressionante per trovare la derivata) i tuoi due lati dell`equazione rispetto a x. L`equazione diventa quindi xf`(x) + 2xf(x) + 6[f(x)]f`(x) = 3 + 2f`(x).

4. Sostituisci di nuovo f(x) con y. Fai attenzione a non farlo con f`(x) poiché è molto diverso da f(x).

5. Risolvi per f`(x). La risposta di questo esempio è (3 - 2xy)/(x + 6y - 2).
Metodo 3 di 4: Derivati superiori

1. Prendere la derivata superiore di una funzione significa semplicemente prendere la derivata della derivata. Ad esempio, se viene richiesta la derivata terza, prendi la derivata della derivata della derivata. Per alcune equazioni, una derivata maggiore diventa uguale a 0.
Metodo 4 di 4: La regola della catena

1. Se y è una funzione differenziabile di z e z è una funzione differenziabile di x, allora y è una funzione composita di x e la derivata di y rispetto a x (dy/dx) è (dy/du)*(du /dx). La regola della catena può anche essere un`equazione composta, come questa: (2x - x). Per trovare la derivata di questo; pensa allo stesso modo in cui lo fai con la linea di prodotti. Moltiplica l`equazione per l`esponente e riduci l`esponente per 1. Quindi moltiplica l`equazione per la derivata che cade sotto l`esponente (in questo caso, 2x^4 - x). La risposta a questo problema diventa quindi 3(2x - x)(8x - 1).
Consigli
- Ogni volta che vedi un problema apparentemente irrisolvibile, non preoccuparti. Prova a dividere il problema in parti più piccole applicando le regole del prodotto, la regola del quoziente, ecc. Quindi differenziare le singole parti.
- Esercitati con la regola del prodotto, la regola del quoziente, la regola della catena e, soprattutto, la differenziazione implicita poiché possono essere piuttosto complicate dal calcolo.
- Conosci la tua calcolatrice; prova le diverse funzioni della calcolatrice per scoprire come funzionano. È certamente prezioso sapere come utilizzare le funzioni tangente e derivata, se la tua calcolatrice le ha.
- Memorizzare le derivate trigonometriche più comunemente usate e come lavorarci.
Avvertenze
- Ricorda che il segno meno è davanti alla f(derivata o g) quando usi la regola del quoziente; questo è un errore comune e si tradurrà in una risposta sbagliata.
Articoli sull'argomento "Determinazione di una derivata"
Condividi sui social network:
Simile
Popolare