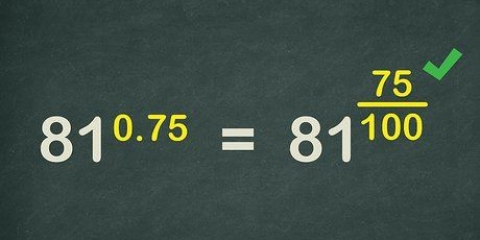Trovare la Derivata della Radice Quadrata di x

Contenuto

Passi

Se hai studiato matematica a scuola, devi aver imparato la regola del potere per determinare la derivata di funzioni semplici. Tuttavia, quando la funzione contiene una radice quadrata o un radicale, ad esempio $\sqrt{X}$ ${sqrt{x}}$ , allora la regola del potere sembra difficile da applicare. Utilizzando una semplice sostituzione di esponenti, determinare la derivata di tale funzione diventa molto semplice. È quindi possibile applicare la stessa sostituzione e utilizzare la regola della catena per trovare la derivata di molte altre funzioni con radici.

Passi

Metodo 1 di 3: Applicazione della regola del potere

Immagine titolata Differenzia la radice quadrata di X Step 1

1. Dai un`altra occhiata alla regola del potere per i derivati. La prima regola che probabilmente hai imparato per trovare derivati è la regola del potere. Questa regola lo dice per una variabile

X

$X$ alla potenza di un numero

un

$un$ , è la derivata ed è calcolata come segue:

$F (X) = X un$ ${displaystyle f(x)=x^{a}}$
$F sesso (X) = un X^{un - 1}$ ${displaystyle f^{prime}(x)=ascia^{a-1}}$
Dai un`occhiata alle seguenti funzioni di esempio e alle loro derivate:

Se $F (X) = X 2$ ${displaystyle f(x)=x^{2}}$ , poi $F sesso (X) = 2 X$ ${displaystyle f^{prime}(x)=2x}$
Se $F (X) = 3 X 2$ ${displaystyle f(x)=3x^{2}}$ , poi $F sesso (X) = 2 * 3 X = 6 X$ ${displaystyle f^{prime}(x)=2*3x=6x}$
Se $F (X) = X 3$ ${displaystyle f(x)=x^{3}}$ , poi $F sesso (X) = 3 X^{2}$ ${displaystyle f^{prime}(x)=3x^{2}}$
Se $F (X) = \frac{1}{2} X^{4}$ ${displaystyle f(x)={frac {1}{2}}x^{4}}$ , poi $F sesso (X) = 4 * \frac{1}{2} X^{3} = 2 X^{3}$ ${displaystyle f^{prime }(x)=4*{frac {1}{2}}x^{3}=2x^{3}}$

Immagine titolata Differenzia la radice quadrata di X Step 2

2. Riscrivi la radice quadrata come esponente. Per trovare la derivata di una funzione radice quadrata, ricorda che la radice quadrata di un numero o di una variabile può essere scritta anche come esponente. Il termine sotto il radicale è scritto come base, ed è elevato alla potenza 1/2. Il termine è usato anche come esponente della radice quadrata. Guarda attraverso i seguenti esempi:

\sqrt{X} = X^{\frac{1}{2}}

${displaystyle {sqrt {x}}=x^{frac {1}{2}}}$

\sqrt{4} = 4^{\frac{1}{2}}

${displaystyle {sqrt {4}}=4^{frac {1}{2}}}$

\sqrt{3 X} = (3 X)^{\frac{1}{2}}

${displaystyle {sqrt {3x}}=(3x)^{frac {1}{2}}}$

Immagine titolata Differenzia la radice quadrata di X Step 3

3. Applicare la regola del potere. Se la funzione è la radice quadrata più semplice,

F (X) = \sqrt{X}

${displaystyle f(x)={sqrt {x}}}$ , quindi applica la regola della potenza come segue per trovare la derivata:

F (X) = \sqrt{X}

${ displaystyle f (x) = { sqrt {x}} }$ (Annotare la funzione originale.)

F (X) = X (\frac{1}{2})

${displaystyle f(x)=x^{({frac {1}{2}})} }$ (Riscrivi la radice come esponente.)

F sesso (X) = \frac{1}{2} X^{(\frac{1}{2} - 1)}

${displaystyle f^{prime }(x)={frac {1}{2}}x^{({frac {1}{2}}-1)} }$ (Trova la derivata usando la regola della potenza.)

F sesso (X) = \frac{1}{2} X^{(- \frac{1}{2})}

${displaystyle f^{prime }(x)={frac {1}{2}}x^{(-{frac {1}{2}})} }$ (Semplifica l`esponente.)

Immagine titolata Differenzia la radice quadrata di X Step 4

4. Semplifica il risultato. A questo punto, dovresti sapere che un esponente negativo significa che prendi l`inverso di quello che sarebbe il numero con l`esponente positivo. L`esponente di

- \frac{1}{2}

${displaystyle -{frac {1}{2}}}$ significa che la radice quadrata della base diventa il denominatore di una frazione.

Continuando con la radice quadrata della funzione x dall`alto, la derivata può essere semplificata come segue:

F sesso (X) = \frac{1}{2} X^{- \frac{1}{2}}

${displaystyle f^{prime }(x)={frac {1}{2}}x^{-{frac {1}{2}}}}$

F sesso (X) = \frac{1}{2} * \frac{1}{\sqrt{X}}

${displaystyle f^{prime }(x)={frac {1}{2}}*{frac {1}{sqrt {x}}}}$

F sesso (X) = 12 \sqrt{X}

${displaystyle f^{prime }(x)={frac {1}{2{sqrt {x}}}}}$

Metodo 2 di 3: Applicazione della regola della catena per le funzioni radice quadrata

Immagine titolata Differenzia la radice quadrata di X Step 5

1. Rivedere la regola della catena per le funzioni. La regola della catena è una regola per le derivate utilizzata quando la funzione originale combina una funzione all`interno di un`altra funzione. La regola della catena dice che, per due funzioni

F (X)

$f(x)$ e

G (X)

${ displaystyle g (x)}$ , la derivata della combinazione delle due funzioni può essere trovata come segue:

Se $y = F (G (X))$ ${ displaystyle y = f (g (x))}$ , poi $y sesso = F^{sesso} (G) * G^{sesso} (X)$ ${ displaystyle y ^ { prime } = f ^ { prime } (g) * g ^ { prime } (x)}$ .

Immagine titolata Differenzia la radice quadrata di X Step 6

2. Definire le funzioni della regola della catena. L`uso della regola della catena richiede di definire prima le due funzioni che compongono la funzione combinata. Per le funzioni radice quadrata, la funzione più esterna è

F (G)

${ displaystyle f (g)}$ la funzione radice quadrata e la funzione più interna

G (X)

${ displaystyle g (x)}$ la funzione sotto il radicale.

Ad esempio: supponiamo di avere la derivata di

\sqrt{3 X + 2}

${displaystyle {sqrt {3x+2}}}$ vuoi trovare. Quindi definisci le due parti come segue:

F (G) = \sqrt{G} = G^{\frac{1}{2}}

${displaystyle f(g)={sqrt {g}}=g^{frac {1}{2}}}$

G (X) = (3 X + 2)

${ displaystyle g(x)=(3x+2)}$

Immagine titolata Differenzia la radice quadrata di X Step 7

3. Trova le derivate delle due funzioni. Per applicare la regola della catena alla radice quadrata di una funzione, devi prima trovare la derivata della funzione radice quadrata generale:

F (G) = \sqrt{G} = G^{\frac{1}{2}}

${displaystyle f(g)={sqrt {g}}=g^{frac {1}{2}}}$

F sesso (G) = \frac{1}{2} G^{- \frac{1}{2}}

${displaystyle f^{prime }(g)={frac {1}{2}}g^{-{frac {1}{2}}}}$

F sesso (G) = 12 \sqrt{G}

${displaystyle f^{prime }(g)={frac {1}{2{sqrt {g}}}}}$

Determinare quindi la derivata della seconda funzione:

G (X) = (3 X + 2)

${ displaystyle g(x)=(3x+2)}$

G sesso (X) = 3

${displaystyle g^{prime}(x)=3}$

Immagine titolata Differenzia la radice quadrata di X Step 8

4. Combina le funzioni nella regola della catena. La regola della catena è

y sesso = F^{sesso} (G) * G^{sesso} (X)

${ displaystyle y ^ { prime } = f ^ { prime } (g) * g ^ { prime } (x)}$ . Combina le derivate come segue:

y sesso = 12 \sqrt{G} * 3

${displaystyle y^{prime }={frac {1}{2{sqrt {g}}}}*3}$

y sesso = 12 \sqrt{(3 X + 2} * 3

${displaystyle y^{prime }={frac {1}{2{sqrt {(3x+2}}}}}*3}$

y sesso = 32 \sqrt{(3 X + 2}

${displaystyle y^{prime }={frac {3}{2{sqrt {(3x+2}}}}}$

Metodo 3 di 3: Trovare rapidamente le derivate delle funzioni radice

Immagine titolata Differenzia la radice quadrata di X Step 9

1. Determina le derivate di una funzione radice quadrata usando un metodo rapido. Quando vuoi trovare la derivata della radice quadrata di una variabile o di una funzione, puoi applicare una semplice regola: la derivata sarà sempre la derivata del numero sotto il radicale, divisa per il doppio della radice quadrata originale. Simbolicamente, questo può essere rappresentato come:

Se $F (X) = \sqrt{voi}$ ${displaystyle f(x)={sqrt {u}}}$ , poi $F sesso (X) = voi sesso 2 \sqrt{voi}$ ${displaystyle f^{prime }(x)={frac {u^{prime }}{2{sqrt {u}}}}}$

Immagine titolata Differenzia la radice quadrata di X Step 10

2. Trova la derivata del numero sotto il radicale. Questo è un numero o una funzione sotto il segno della radice quadrata. Per utilizzare questo metodo rapido, trova la derivata del numero sotto il radicale. Dai un`occhiata ai seguenti esempi:

Nella funzione

\sqrt{5 X + 2}

${displaystyle {sqrt {5x+2}}}$ , è il numero radice

(5 X + 2)

${ displaystyle (5x+2)}$ . La derivata è

5

$5$ .

Nella funzione

\sqrt{3 X} 4

${displaystyle {sqrt {3x^{4}}}}$ , è il numero radice

3 X 4

${displaystyle 3x^{4}}$ . La derivata è

12 X 3

${displaystyle 12x^{3}}$ .

Nella funzione

\sqrt{S io n (X)}

${ displaystyle { sqrt {peccato (x)}}}$ , è il numero radice

peccato (X)

${ displaystyle sin(x)}$ . La derivata è

\cos (X)

${ displaystyle cos (x)}$ .

Immagine titolata Differenzia la radice quadrata di X Step 11

3. Scrivi la derivata del numero radice come numeratore di una frazione. La derivata di una funzione radice quadrata conterrà una frazione. Il numeratore di questa frazione è la derivata del numero radice. Quindi, nelle funzioni di esempio sopra, la prima parte della derivata sarà così:

F (X) = \sqrt{5 X + 2}

${displaystyle f(x)={sqrt {5x+2}}}$ , poi

F sesso (X) = \frac{5}{denominatore}

${displaystyle f^{prime}(x)={frac {5}{text{denominatore}}}}$

F (X) = \sqrt{3 X} 4

${displaystyle f(x)={sqrt {3x^{4}}}}$ , poi

F sesso (X) = 12 X 3 denominatore

${displaystyle f^{prime }(x)={frac {12x^{3}}{text{denominatore}}}}$

F (X) = \sqrt{peccato (X)}

${displaystyle f(x)={sqrt { sin(x)}}}$ , poi

F sesso (X) = \cos (X) denominatore

${displaystyle f^{prime}(x)={frac {cos(x)}{text{denominatore}}}}$

Immagine titolata Differenzia la radice quadrata di X Step 12

4. Scrivi il denominatore come il doppio della radice quadrata originale. Con questo metodo rapido, il denominatore è il doppio della funzione radice quadrata originale. Quindi nelle tre funzioni di esempio sopra, i denominatori delle derivate sono:

F (X) = \sqrt{5 X + 2}

${displaystyle f(x)={sqrt {5x+2}}}$ , poi

F sesso (X) = contatore 2 \sqrt{5 X + 2}

${displaystyle f^{prime }(x)={frac {text{contatore}}{2{sqrt {5x+2}}}}}$

F (X) = \sqrt{3 X} 4

${displaystyle f(x)={sqrt {3x^{4}}}}$ , poi

F sesso (X) = contatore 2 \sqrt{3 X} 4

${displaystyle f^{prime }(x)={frac {text{contatore}}{2{sqrt {3x^{4}}}}}}}$

F (X) = \sqrt{peccato (X)}

${displaystyle f(x)={sqrt { sin(x)}}}$ , poi

F sesso (X) = contatore 2 \sqrt{peccato (X)}

${displaystyle f^{prime }(x)={frac {text{contatore}}{2{sqrt {sin(x)}}}}}$

Immagine titolata Differenzia la radice quadrata di X Step 13

5. Combina numeratore e denominatore per trovare la derivata. Metti insieme le due metà della frazione e il risultato sarà la derivata della funzione originale.