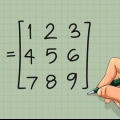Determinare il Determinante di una Matrice 3x3: 12 Passaggi (con Immagini)

Contenuto

Passi
- Parte 1 di 2: Determinazione del determinante
- Parte 2 di 2: Semplificare il problema
Consigli

Il determinante di una matrice è ampiamente utilizzato in matematica, algebra lineare e geometria superiore. Al di fuori del mondo scientifico, ingegneri e programmatori di computer grafica utilizzano frequentemente i determinanti delle matrici. Leggi questo articolo per determinare il determinante di una matrice 3x3.

Passi

Parte 1 di 2: Determinazione del determinante

Immagine titolata Trova il determinante di una matrice 3X3 Step 1

1. Scrivi la tua matrice 3 x 3. Iniziamo con una matrice 3 x 3 A e proviamo il determinante |A| piacergli. Usiamo la seguente notazione generale per la matrice (e questa è la nostra matrice di esempio):

$m = (\begin{matrix} un \end{matrix} 11 {un}_{12} {un}_{13} {un}_{21} & {un}_{22} & {un}_{23} {un}_{31} & {un}_{32} & {un}_{33}) = (\begin{matrix} 1 & 5 & 3 \\ 2 & 4 & 7 \\ 4 & 6 & 2 \end{matrix})$ $M={begin{pmatrix}a_{{11}}&a_{{12}}&a_{{13}}\a_{{21}}&a_{{22}}&a_{ {23}}\a_{{31}}&a_{{32}}&a_{{33}}end{pmatrix}}={begin{pmatrix}1&5&3\2& 4&7\4&6&2end{pmatrice}}$

Immagine titolata Trova il determinante di una matrice 3X3 Step 2

2. Scegli una riga o una colonna. Questa sarà la tua riga o colonna di riferimento. Otterrai la stessa risposta, indipendentemente da quale scegli. Ora scegli la prima riga. Successivamente ti consiglieremo su come scegliere l`opzione più facile da calcolare.

Scegliamo la prima riga della nostra matrice di esempio A. Cerchia 1 5 3. In termini generali, cerchio a₁₁ un₁₂ un₁₃.

Immagine titolata Trova il determinante di una matrice 3X3 Step 3

3. Cancella la riga e la colonna del primo elemento. Guarda la riga o la colonna che hai cerchiato e seleziona il primo elemento. Disegna una linea attraverso la riga e la colonna corrispondenti. Se tutto va bene, questo ora produce quattro numeri. Lo trattiamo come una matrice 2 x 2.

Nel nostro esempio, la riga di riferimento è 1 5 3. Esso primo elemento è nella riga 1 e nella colonna 1. Cancella completamente la riga 1 e la colonna 1. Annota gli elementi rimanenti come aMatrice 2x2:

~~1 5 3~~
2 4 7
4 6 2

Immagine titolata Trova il determinante di una matrice 3X3 Step 4

4. Determina il determinante della matrice 2 x 2. Non dimenticare: la matrice

(\begin{matrix} un & B \\ C & D \end{matrix})

${begin{pmatrix}a&b\c&dend{pmatrix}}$ ha un determinante di ad - ac. Lo sai disegnando una croce (X) attraverso la matrice 2 x 2. Moltiplica i due numeri collegati per della X. Quindi sottrarre il prodotto dei due numeri collegati da /. Usa questa formula per calcolare il determinante della matrice che hai appena trovato.

Nel nostro esempio, il determinante della matrice è

(\begin{matrix} 4 & 7 \\ 6 & 2 \end{matrix})

${begin{pmatrix}4&7\6&2end{pmatrix}}$ = 4 * 2 - 7 * 6 = -34.

Questo determinante è chiamato il minore dell`elemento che abbiamo scelto nella nostra matrice originale. In questo caso abbiamo il minore di un₁₁ trovato.

Immagine titolata Trova il determinante di una matrice 3X3 Step 5

5. Moltiplica la risposta per l`elemento scelto. Ricorda che hai selezionato un elemento dalla tua riga (o colonna) di riferimento quando hai deciso quale riga e colonna barrare. Moltiplica questo elemento per il determinante che hai appena calcolato per la matrice 2x2.

Nel nostro esempio abbiamo a₁₁ selezionato, che ha valore 1. Moltiplica questo per -34 (il determinante della matrice 2x2) per ottenere 1*-34 = -34 ottenere.

Immagine titolata Trova il determinante di una matrice 3X3 Step 6

6. Determina il segno della tua risposta. Ora moltiplica la risposta per 1 o per -1 per ottenere il cofattore dell`elemento prescelto. Quello che usi dipende dalla posizione dell`elemento nella matrice 3x3. Memorizza la seguente semplice tabella per scoprire quale elemento causa cosa:

+ - +
- + -
+ - +

Perché noi un₁₁ abbiamo scelto, contrassegnato con un +, moltiplichiamo il numero per +1 (in altre parole, non ci facciamo niente). La risposta è ancora -34.

Un altro modo per determinare il segno è con la formula (-1), dove io e J formano la riga e la colonna dell`elemento.

Immagine titolata Trova il determinante di una matrice 3X3 Step 7

7. Ripetere questa procedura per il secondo elemento nella riga o colonna di riferimento. Continua con la matrice 3x3 originale, con la riga o la colonna che hai cerchiato in precedenza. Ripeti la stessa procedura con questo elemento:

Attraversa la riga e la colonna di quell`elemento. In questo caso si seleziona l`elemento a₁₂ (con valore 5). Incrocia la prima riga (1 5 3) e la seconda colonna

(\begin{matrix} 5 \\ 4 \\ 6 \end{matrix})

${begin{pmatrix}5\4\6end{pmatrix}}$ .

Tratta gli elementi rimanenti come una matrice 2x2. Nel nostro esempio, la matrice è

(\begin{matrix} 2 & 7 \\ 4 & 2 \end{matrix})

${begin{pmatrix}2&7\4&2end{pmatrix}}$

Determina il determinante di questa matrice 2x2. Usa la formula ad - bc. (2*2 - 7*4 = -24)

Moltiplica questo per l`elemento scelto della matrice 3x3. -24 * 5 = -120

Determina se moltiplicare per -1. Usa la tabella dei caratteri o la formula (-1). Abbiamo l`elemento a₁₂ scelto, e questo è un – sulla tabella dei caratteri. Dobbiamo cambiare il segno della nostra risposta: (-1)*(-120) = 120.

Immagine titolata Trova il determinante di una matrice 3X3 Step 8

8. Ripetere per il terzo elemento. Ora devi trovare un cofattore. Calcola i per il terzo termine nella riga o colonna di riferimento. Ecco una rapida spiegazione di come calcolare il cofattore di ₁₃ nel nostro esempio:

Incrocia la riga 1 e la colonna 3 e ottieni

(\begin{matrix} 2 & 4 \\ 4 & 6 \end{matrix})

${begin{pmatrix}2&4\4&6end{pmatrix}}$

Il suo determinante è 2*6 - 4*4 = -4.

Moltiplica questo per l`elemento a₁₃: -4 * 3 = -12.

elemento a₁₃ è un + sulla tabella dei caratteri, quindi la risposta è -12.

Immagine titolata Trova il determinante di una matrice 3X3 Step 9

9. Somma i tre risultati insieme. Questo è il passo finale. Hai calcolato i cofattori, uno per ogni elemento in una singola riga o colonna. Somma questi insieme e hai trovato il determinante della matrice 3x3.

Nel nostro esempio, il determinante è -34 + 120 + -12 = 74.

Parte 2 di 2: Semplificare il problema

Immagine titolata Trova il determinante di una matrice 3X3 Step 10

1. Scegli il riferimento con il maggior numero di zeri. Non dimenticarlo tu ogni può scegliere riga o colonna come riferimento. Otterrai la stessa risposta, qualunque cosa tu scelga. Se scegli una riga o una colonna con zeri, devi solo calcolare il cofattore degli elementi che non sono zero. Il motivo è il seguente:

Supponiamo di scegliere la riga 2, con gli elementi a₂₁, un₂₂, e un₂₃. Per risolvere questo problema osserviamo tre diverse matrici 2x2. Supponiamo di chiamarla A₂₁, un₂₂ e A₂₃.
Il determinante della matrice 3x3 è a₂₁|A₂₁| - un₂₂|A₂₂| + un₂₃|A₂₃|.
Se i termini a₂₂ e un₂₃ sono entrambi 0, allora la nostra formula diventa₂₁|A₂₁| - 0*|A₂₂| + 0*|A₂₃| = a₂₁|A₂₁| - 0 + 0 = a₂₁|A₂₁|. Ora non resta che calcolare il cofattore di un singolo elemento.

Immagine titolata Trova il determinante di una matrice 3X3 Step 11

2. Somma le righe per semplificare la matrice. Se prendi i valori di una riga e li aggiungi a un`altra riga, il determinante della matrice non cambierà. Lo stesso vale per le colonne. Puoi farlo ripetutamente - o moltiplicare i valori per una costante prima di sommare - per ottenere il maggior numero possibile di zeri nella matrice. Questo può farti risparmiare un sacco di lavoro.

Ad esempio, supponiamo di avere una matrice 3x3:

(\begin{matrix} 9 & - 1 & 2 \\ 3 & 1 & 0 \\ 7 & 5 & - 2 \end{matrix})

${begin{pmatrix}9&-1&2\3&1&0\7&5&-2end{pmatrix}}$

Ogni 9 in posizione a₁₁ per eliminarlo, possiamo moltiplicare la seconda riga per -3 e aggiungere il risultato alla prima. La nuova prima riga diventa quindi [9 -1 2] + [-9 -3 0] = [0 -4 2].

La nuova matrice è

(\begin{matrix} 0 & - 4 & 2 \\ 3 & 1 & 0 \\ 7 & 5 & - 2 \end{matrix})

${begin{pmatrix}0&-4&2\3&1&0\7&5&-2end{pmatrix}}$ Prova a usare lo stesso trucco per le colonne, a₁₂ per fare uno 0.

Immagine titolata Trova il determinante di una matrice 3X3 Step 12

3. Impara il trucco per risolvere le matrici triangolari. In questi casi speciali, il determinante è semplicemente il prodotto degli elementi lungo la diagonale principale, da a₁₁ in alto a sinistra ad a₃₃ in basso a destra. Stiamo ancora parlando di matrici 3x3, ma le matrici "triangolari" hanno schemi di valori speciali che non zero sono:

Matrice del triangolo superiore: tutti gli elementi diversi da zero si trovano sopra o sopra la diagonale principale. Tutti i valori sottostanti sono zero.

Matrice triangolo inferiore: tutti gli elementi diversi da zero si trovano sopra o sotto la diagonale principale.

Matrice diagonale: tutti gli elementi diversi da zero si trovano sulla diagonale principale. (Un sottoinsieme di quanto sopra.)

Consigli

Questo metodo può essere utilizzato per matrici quadrate di qualsiasi dimensione. Ad esempio, se lo usi per una matrice 4x4, mantieni dopo il "barrare" una matrice 3x3, per la quale è possibile calcolare il determinante come indicato sopra. Attenzione, perché farlo a mano sarà molto noioso!
Se tutti gli elementi di una riga o di una colonna sono uguali a 0, il determinante di quella matrice è uguale a 0.