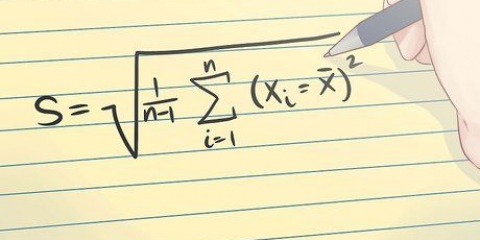Determinazione del Coefficiente di Correlazione

Contenuto

Passi
Consigli
Avvertenze

Il coefficiente di correlazione, indicato come r o ρ, è la misura della correlazione lineare (la relazione, sia in forza che in direzione) tra due variabili. Va da -1 a +1, utilizzando i segni più e meno per rappresentare la correlazione positiva e negativa. Se il coefficiente di correlazione è esattamente -1, allora la relazione tra le due variabili è completamente negativa; se il coefficiente di correlazione è esattamente +1, allora la relazione è completamente positiva. Due variabili possono avere una correlazione positiva, una correlazione negativa o nessuna correlazione. Puoi calcolare la correlazione a mano, utilizzando alcuni calcolatori di correlazione gratuiti disponibili online, oppure utilizzando le funzioni statistiche di una buona calcolatrice grafica.

Passi

Metodo 1 di 4: Calcolo manuale del coefficiente di correlazione

Immagine titolata Find the Correlation Coefficient Step 1

1. Raccogli prima i tuoi dati. Per iniziare a calcolare una correlazione efficiente, esamina prima le coppie di dati. È utile metterli in una tabella, sia verticalmente che orizzontalmente. Etichetta ogni riga o colonna x e y.

Ad esempio: supponiamo di avere quattro coppie di dati per X e y. La tabella potrebbe quindi apparire così:

x || y
1 || 1
2 || 3
4 || 5
5 || 7

Immagine titolata Find the Correlation Coefficient Step 2

2. Calcola la media di X. Per calcolare la media, devi sommare tutti i valori di X aggiungi e poi dividi per il numero di valori.

Partendo dall`esempio sopra, nota che hai quattro valori per X. Per calcolare la media, conta tutti i valori per X e dividilo per 4. Il calcolo quindi si presenta così:

μ X = (1 + 2 + 4 + 5) / 4

${displaystyle mu _{x}=(1+2+4+5)/4}$

μ X = 12 / 4

${displaystyle mu _{x}=12/4}$

μ X = 3

${displaystyle mu _{x}=3}$

Immagine titolata Find the Correlation Coefficient Step 3

3. Trova la media di y. Per ottenere la media di y Per trovarlo, segui gli stessi passaggi, sommando tutti i valori di y insieme e poi dividendo per il numero di valori.

Nell`esempio sopra, hai anche quattro valori per y. Somma tutti questi valori e poi dividi per 4. I calcoli saranno quindi simili a questo:

μ y = (1 + 3 + 5 + 7) / 4

${displaystyle mu _{y}=(1+3+5+7)/4}$

μ y = 16 / 4

${displaystyle mu _{y}=16/4}$

μ y = 4

${displaystyle mu _{y}=4}$

Immagine titolata Find the Correlation Coefficient Step 4

4. Determina la deviazione standard di X. Una volta che hai i tuoi mezzi, puoi calcolare la deviazione standard. Usa la formula per questo:

Σ X = \sqrt{} 1 n - 1 Σ (X - μ_{X})^{2}

${displaystyle sigma _{x}={sqrt {{frac {1}{n-1}}Sigma (x-mu _{x})^{2}}}}$

Con i dati di esempio, i tuoi calcoli saranno simili a questo:

Σ X = \sqrt{} 1 4 - 1 * ((1 - 3)^{2} + (2 - 3)^{2} + (4 - 3)^{2} + (5 - 3)^{2})

${displaystyle sigma _{x}={sqrt {{frac {1}{4-1}}*((1-3)^{2}+(2-3)^{2}+(4 -3)^{2}+(5-3)^{2})}}}$

Σ X = \sqrt{} \frac{1}{3} * (4 + 1 + 1 + 4)

${displaystyle sigma _{x}={sqrt {{frac {1}{3}}*(4+1+1+4)}}}$

Σ X = \sqrt{} \frac{1}{3} * (10)

${displaystyle sigma _{x}={sqrt {{frac {1}{3}}*(10)}}}$

Σ X = \sqrt{\frac{10}{3}}

${displaystyle sigma _{x}={sqrt {frac {10}{3}}}}$

Σ X = 1, 83

${ displaystyle sigma _ {x} = 1,83}$

Immagine titolata Find the Correlation Coefficient Step 5

5. Calcola la deviazione standard di y. Utilizzando gli stessi passaggi di base, trova la deviazione standard di y. Utilizzerai la stessa formula, usando i punti dati per y.

Con i dati di esempio, i tuoi calcoli saranno simili a questo:

Σ y = \sqrt{} 1 4 - 1 * ((1 - 4)^{2} + (3 - 4)^{2} + (5 - 4)^{2} + (7 - 4)^{2})

${displaystyle sigma _{y}={sqrt {{frac {1}{4-1}}*((1-4)^{2}+(3-4)^{2}+(5 -4)^{2}+(7-4)^{2})}}}$

Σ y = \sqrt{} \frac{1}{3} * (9 + 1 + 1 + 9)

${displaystyle sigma _{y}={sqrt {{frac {1}{3}}*(9+1+1+9)}}}$

Σ y = \sqrt{} \frac{1}{3} * (20)

${displaystyle sigma _{y}={sqrt {{frac {1}{3}}*(20)}}}$

Σ y = \sqrt{\frac{20}{3}}

${displaystyle sigma _{y}={sqrt {frac {20}{3}}}}$

Σ y = 2, 58

${ displaystyle sigma _ {y} = 2,58}$

Immagine titolata Find the Correlation Coefficient Step 6

6. Visualizza la formula di base per determinare un coefficiente di correlazione. La formula per calcolare un coefficiente di correlazione utilizza medie, deviazioni standard e il numero di coppie in un set di dati (rappresentato da n). Il coefficiente di correlazione stesso è rappresentato dalla lettera minuscola r o dalla lettera greca ρ (rho). Per questo articolo, utilizzeremo la formula nota come coefficiente di correlazione di Pearson come mostrato di seguito:

ρ = (1 n - 1) Σ (X - μ X Σ_{X}) * (y - μ y Σ_{y})

${displaystyle rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}} }right)*left({frac {y-mu _{y}}{sigma _{y}}}right)}$

Si possono notare leggere variazioni nella formula, qui o in altre spiegazioni. Ad esempio, alcuni useranno la notazione greca con rho e sigma, mentre altri useranno r e s. Alcune spiegazioni possono utilizzare formule leggermente diverse, ma saranno matematicamente equivalenti a questa.

Immagine titolata Find the Correlation Coefficient Step 7

7. Determina il coefficiente di correlazione. Ora hai le medie e le deviazioni standard per le tue variabili, quindi puoi passare alla formula del coefficiente di correlazione. Ricordati che n rappresenta il numero di valori che hai. Hai già elaborato le altre informazioni rilevanti nei passaggi precedenti.

Utilizzando i dati di esempio, è possibile inserire i dati nella formula del coefficiente di correlazione e calcolarli in questo modo:

ρ = (1 n - 1) Σ (X - μ X Σ_{X}) * (y - μ y Σ_{y})

${displaystyle rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}} }right)*left({frac {y-mu _{y}}{sigma _{y}}}right)}$

ρ = (\frac{1}{3}) *

${displaystyle rho =left({frac {1}{3}}right)*}$ [

(1 - 3 1, 83) * (1 - 4 2, 58) + (2 - 3 1, 83) * (3 - 4 2, 58)

${displaystyle left({frac {1-3}{1.83}}right)*left({frac {1-4}{2.58}}right)+left({ frac {2- 3}{1.83}}destra)*sinistra({frac {3-4}{2.58}}destra)}$

+ (4 - 3 1, 83) * (5 - 4 2, 58) + (5 - 3 1, 83) * (7 - 4 2, 58)

${displaystyle +left({frac {4-3}{1.83}}right)*left({frac {5-4}{2.58}}right)+left({ frac {5 -3}{1.83}}destra)*sinistra({frac {7-4}{2.58}}destra)}$ ]

ρ = (\frac{1}{3}) * (6 + 1 + 1 + 6 4, 721)

${displaystyle rho =left({frac {1}{3}}right)*left({frac {6+1+1+6}{4,721}}right)}$

ρ = (\frac{1}{3}) * 2, 965

${displaystyle rho =left({frac {1}{3}}right)*2.965}$

ρ = (2, 965 3)

${displaystyle rho =left({frac {2.965}{3}}right)}$

ρ = 0, 988

${ displaystyle rho = 0,988}$

Immagine titolata Find the Correlation Coefficient Step 8

8. Interpreta il risultato. Per questo set di dati, il coefficiente di correlazione è 0,988. Questo numero ti dice due cose sui dati. Guarda il segno del numero e la dimensione del numero.

Poiché il coefficiente di correlazione è positivo, si può dire che esiste una correlazione positiva tra i dati x e i dati y. Ciò significa che all`aumentare dei valori x, ti aspetti che aumentino anche i valori y.

Poiché il coefficiente di correlazione è molto vicino a +1, i dati x e y sono strettamente correlati. Se dovessi rappresentare graficamente questi punti, vedresti che sono un`ottima approssimazione di una retta.

Metodo 2 di 4: utilizzo dei calcolatori di correlazione online

Immagine titolata Find the Correlation Coefficient Step 9

1. Cerca online i calcolatori di correlazione. La misurazione della correlazione è un calcolo abbastanza standard per gli statistici. Il calcolo può diventare molto noioso per set di dati di grandi dimensioni se eseguito a mano. Pertanto, molte fonti hanno reso disponibili online i calcoli di correlazione comuni. Usa qualsiasi motore di ricerca e inserisci il termine di ricerca "calcolatore di correlazione".

Immagine titolata Find the Correlation Coefficient Step 10

2. Per i dati in. Si prega di leggere attentamente le istruzioni sul sito web in modo da poter inserire correttamente i dati. È importante che le coppie di dati siano mantenute in ordine o otterrai un risultato di correlazione errato. Diversi siti Web utilizzano una formattazione diversa per inserire i dati.

Ad esempio: sul sito web http://ncalcolatori.com/statistics/calcolatore del coefficiente di correlazione.htm trova una casella orizzontale per inserire i valori x e una seconda casella orizzontale per inserire i valori y. Inserisci i termini separati solo da virgole. Quindi il set di dati x calcolato in precedenza in questo articolo deve essere inserito come 1,2,4,5. Il set di dati y viene inserito come 1,3,5,7.

Su un altro sito, http://www.alcol.com/calcolatori/statistica/coefficiente-di-correlazione/, puoi inserire i dati sia orizzontalmente che verticalmente, purché mantieni i punti dati in ordine.

Immagine titolata Find the Correlation Coefficient Step 11

3. Calcola i risultati. Questi siti di calcolo sono popolari perché, in generale, dopo aver inserito i dati, tutto ciò che devi fare è fare clic sul pulsante "Calcola": il risultato apparirà automaticamente.

Metodo 3 di 4: Utilizzo di una calcolatrice grafica

Immagine titolata Find the Correlation Coefficient Step 12

1. Inserisci i tuoi dati. Sulla tua calcolatrice grafica, attiva la funzione statistica e quindi seleziona il comando `Modifica`.

Ogni calcolatrice ha comandi chiave leggermente diversi. Questo articolo fornisce istruzioni specifiche per Texas Instruments TI-86.
Entra nella funzione Stat premendo [2nd]-Stat (sopra il tasto `+`) e poi F2-Edit.

Immagine titolata Find the Correlation Coefficient Step 13

2. Cancella tutti i vecchi dati salvati. La maggior parte dei calcolatori manterrà i dati statistici fino a quando non saranno cancellati. Per assicurarti di non confondere i vecchi dati con i nuovi dati, devi prima cancellare tutte le informazioni memorizzate in precedenza.

Utilizzare i tasti freccia per spostare il cursore per evidenziare la categoria `xStat`. Quindi premere `Cancella` e `Invio. Questo dovrebbe cancellare tutti i valori nella colonna xStat.

Usa i tasti freccia per evidenziare la categoria `yStat`. Premi "Cancella" e "Invio" per cancellare i dati anche da quella colonna.

Immagine titolata Find the Correlation Coefficient Step 14

3. Inserisci i valori dei tuoi dati. Utilizzare i tasti freccia per spostare il cursore sul primo spazio sotto l`intestazione xStat. Digita il tuo primo valore di dati e quindi premi Invio. Dovresti vedere lo spazio nella parte inferiore dello schermo `xStat(1)=__` dove il tuo valore riempie lo spazio vuoto. Quando premi Invio, i dati riempiranno la tabella, il cursore si sposterà alla riga successiva e la riga nella parte inferiore dello schermo dovrebbe ora leggere `xStat(2)=__`.

Continua a inserire tutti i valori x.

Una volta inseriti i valori x, utilizzare i tasti freccia per passare alla colonna yStat e inserire i valori y.

Quando tutti i dati sono stati inseriti, premere Esci per cancellare lo schermo e uscire dal menu Stat.

Immagine titolata Find the Correlation Coefficient Step 15

4. Calcola le statistiche di regressione lineare. Il coefficiente di correlazione è una misura di quanto bene i dati approssimano una linea retta. Una calcolatrice grafica con funzioni statistiche può calcolare molto rapidamente la linea di adattamento migliore e il coefficiente di correlazione.

Entra nella funzione Stat e poi premi il pulsante Calc. Sulla TI-86 questo è [2nd][Stat][F1].

Scegli i calcoli di regressione lineare. Sulla TI-86, è [F3], etichettato "LinR.` Lo schermo grafico mostrerà quindi la riga `LinR _` con un cursore lampeggiante.

Ora devi inserire i nomi delle due variabili che vuoi calcolare. Questi sono xStat e yStat.

Sulla TI-86, selezionare l`elenco dei nomi ("Nomi") premendo [2nd][List][F3].

La riga inferiore dello schermo dovrebbe ora mostrare le variabili disponibili. Scegli [xStat] (questo è probabilmente il pulsante F1 o F2), quindi inserisci una virgola e poi [yStat].

Premere Invio per calcolare i dati

Immagine titolata Find the Correlation Coefficient Step 16

5. Interpreta i risultati. Quando si preme Invio, la calcolatrice calcolerà immediatamente le seguenti informazioni per i dati inseriti:

y = un + B X

${ displaystyle y=a+bx}$ : Questa è la formula generale per una retta. Tuttavia, invece del noto `y=mx+b`, questo viene presentato in ordine inverso.

un =

${displaystyle a=}$ . Questo è il valore dell`intersezione con l`asse y della linea che si adatta meglio.

B =

${displaystyle b=}$ . Questa è la pendenza della linea che si adatta meglio.

corretta =

${displaystyle {text{corr}}=}$ . Questo è il coefficiente di correlazione.

n =

${displaystyle n=}$ . Questo è il numero di coppie di dati utilizzate nel calcolo.

Metodo 4 di 4: ripetere le basi

Immagine titolata Find the Correlation Coefficient Step 17

1. Comprendere il concetto di correlazione. La correlazione si riferisce alla relazione statistica tra due grandezze. Il coefficiente di correlazione è un singolo numero che puoi calcolare per due serie di punti dati. Il numero è sempre compreso tra -1 e +1 e indica quanto strettamente sono collegati i due set di dati.

Ad esempio, se hai misurato l`altezza e l`età dei bambini fino a circa 12 anni, ti aspetteresti di trovare una forte correlazione positiva. Man mano che i bambini crescono, tendono a diventare più alti.
Un esempio di correlazione negativa è confrontare il tempo che qualcuno trascorre a praticare il golf e il punteggio di golf di quella persona. Con il progredire della pratica, il punteggio dovrebbe diminuire.
In definitiva, ti aspetteresti poca correlazione, positiva o negativa, tra il numero di scarpe di una persona, ad esempio, e i voti degli esami.

Immagine titolata Find the Correlation Coefficient Step 18

2. Calcola la media. La media aritmetica, o "media", di un insieme di dati viene calcolata sommando tutti i valori dei dati insieme e quindi dividendo per il numero di valori nell`insieme. Quando vuoi determinare il coefficiente di correlazione per i tuoi dati, devi calcolare la media di ogni set di dati.

La media di una variabile è indicata dalla variabile con una linea orizzontale sopra di essa. Questo è spesso indicato come "x-bar" o "y-bar" per i set di dati di x e y. In alternativa, la media può essere indicata dalla lettera greca minuscola μ (mu). Ad esempio, per rappresentare la media dei punti dati di x, puoi usare μ_X o μ(x).

Ad esempio, se hai un insieme di x (1,2,5,6,9,10), la media di questi dati verrebbe calcolata come segue:

μ X = (1 + 2 + 5 + 6 + 9 + 10) / 6

${displaystyle mu _{x}=(1+2+5+6+9+10)/6}$

μ X = 33 / 6

${displaystyle mu _{x}=33/6}$

μ X = 5, 5

${displaystyle mu _{x}=5,5}$

Immagine titolata Find the Correlation Coefficient Step 19

3. Conoscere l`importanza della deviazione standard. Nelle statistiche, la deviazione standard misura la variazione, mostrando lo spread dei numeri rispetto alla media. Un gruppo di numeri con una deviazione standard bassa sono abbastanza vicini tra loro. Un gruppo di numeri con una deviazione standard elevata è più disperso.

Come simbolo, la deviazione standard è espressa con la lettera minuscola s o la lettera greca σ (sigma). Quindi la deviazione standard dei dati x viene scritta come S_X o_X.

Immagine titolata Find the Correlation Coefficient Step 20

4. Riconosci la notazione della sommatoria. L`operatore di somma è uno degli operatori più comuni in matematica, che rappresenta una somma di valori. È rappresentato dalla lettera maiuscola greca, sigma o ∑.

Ad esempio, se hai un insieme di punti dati x (1,2,5,6,9,10), allora ∑x significa:

1+2+5+6+9+10 = 33

Consigli

Il coefficiente di correlazione è talvolta indicato come "coefficiente di correlazione momento-prodotto Pearson", in onore di Karl Pearson, il suo sviluppatore.
In generale, un coefficiente di correlazione maggiore di 0,8 (positivo o negativo) rappresenta una forte correlazione; un coefficiente di correlazione inferiore a 0,5 (sempre positivo o negativo) rappresenta un coefficiente di correlazione debole.

Avvertenze

La correlazione mostra che due insiemi di dati sono in qualche modo collegati. Tuttavia, fai attenzione a non interpretarlo come una relazione causale. Ad esempio, se confronti le dimensioni delle scarpe delle persone e la loro altezza, probabilmente troverai una forte correlazione positiva. Le persone più grandi generalmente hanno i piedi più grandi. Tuttavia, questo non significa che diventare alti ti farà crescere i piedi, o che i piedi grandi ti faranno diventare alto. Succedono solo insieme.