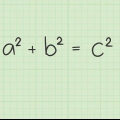Ad esempio: hai un triangolo con una base di 15 centimetri e un triangolo corrispondente con una base lunga 10 cm. 
Ad esempio, se riduci un triangolo con base 15 cm a un triangolo con base 10 cm, il rapporto è  .
.
Inserendo i valori corretti, questo diventa .
. 
Ad esempio: il rapporto  può essere semplificato a
può essere semplificato a . Quindi il fattore di scala di due triangoli, uno con base di 15 cm e uno con base di 10 cm, è
. Quindi il fattore di scala di due triangoli, uno con base di 15 cm e uno con base di 10 cm, è  .
. 

Ad esempio, con un fattore di scala 2 ingrandisci la figura. 
Ad esempio, se l`ipotenusa di un triangolo rettangolo è lunga 5 centimetri e il fattore di scala è 2, per determinare l`ipotenusa del triangolo corrispondente, si calcola  . Quindi il triangolo scalato ha un`ipotenusa di 10 cm.
. Quindi il triangolo scalato ha un`ipotenusa di 10 cm. 
Ad esempio, se la base di un triangolo rettangolo è 3 cm, con un fattore di scala di 2, si calcola  per la base del triangolo scalato. Se l`altezza di un triangolo rettangolo è lungo 4 cm, con un fattore di scala di 2, allora calcola
per la base del triangolo scalato. Se l`altezza di un triangolo rettangolo è lungo 4 cm, con un fattore di scala di 2, allora calcola  per l`altezza del triangolo scalato.
per l`altezza del triangolo scalato. 

Le figure irregolari possono essere ridimensionate se i loro lati sono tutti proporzionali. Quindi puoi calcolare un fattore di scala utilizzando qualsiasi dimensione data. Poiché conosci la larghezza di qualsiasi poligono, puoi creare un`equazione di rapporto. Aumentando si usa il rapporto  . Se hai intenzione di ridurre, usa il rapporto
. Se hai intenzione di ridurre, usa il rapporto  .
. Semplifica il rapporto. Il rapporto  può essere semplificato a
può essere semplificato a  . Il rapporto
. Il rapporto  può essere semplificato a
può essere semplificato a  . Quindi i due poligoni irregolari hanno un fattore di scala di
. Quindi i due poligoni irregolari hanno un fattore di scala di  o
o  .
. 
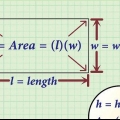
Moltiplica l`altezza del rettangolo ABCD per il fattore di scala. Questo ti darà l`altezza del rettangolo EFGH:  .
. Moltiplica la larghezza del rettangolo ABCD per il fattore di scala. Questo ti darà la larghezza del rettangolo EFGH:  .
. Moltiplica l`altezza e la larghezza del rettangolo EFGH per l`area:  . Quindi, l`area del rettangolo EFGH è di 150 cm2.
. Quindi, l`area del rettangolo EFGH è di 150 cm2. 

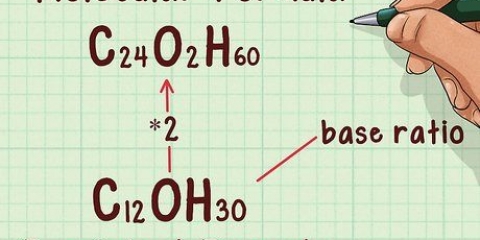
Ad esempio: per determinare la formula molecolare della sostanza in questione, moltiplicare il pedice di H2O per il fattore di scala 3. H2O * 3 = H6O3 
Ad esempio: il fattore di scala per la connessione è 3. La formula molecolare della sostanza è H6O3.
Determinazione del fattore di scala
Contenuto
Il fattore di scala (lineare) è il rapporto di due lati corrispondenti di figure della stessa forma. Figure simili hanno la stessa forma ma dimensioni diverse. Il fattore di scala viene utilizzato per risolvere semplici problemi geometrici. È possibile utilizzare il fattore di scala per determinare i lati sconosciuti di una figura. Al contrario, puoi utilizzare la lunghezza del lato di due numeri simili per calcolare il fattore di scala. Tali problemi richiedono di moltiplicare o semplificare le frazioni.
Passi
Metodo 1 di 4: Determinazione del fattore di scala di una figura in scala

1. Controlla se le cifre sono simili. Figure della stessa forma hanno gli stessi angoli e le lunghezze dei lati sono proporzionali. Figure simili hanno la stessa forma, ma una figura è più grande dell`altra.
- La dichiarazione deve indicare che le forme sono uguali, o mostrare che gli angoli sono gli stessi, altrimenti indicare che il rapporto di lunghezza dei lati è proporzionale, alla scala, o che corrispondono tra loro.

2. Trova un lato corrispondente di ogni figura. Potrebbe essere necessario ruotare o capovolgere la figura in modo che le due forme si allineino e riconosci i lati corrispondenti. La lunghezza di questi due lati deve essere data, oppure devi essere in grado di misurarli. Se non si conosce la lunghezza del lato di ciascuna figura, non è possibile trovare il fattore di scala.

3. Stabilisci il rapporto. Per ogni coppia di figure corrispondenti, ci sono due fattori di scala: uno che usi quando ingrandisci una figura e uno che usi quando rimpicciolisci. Se ingrandisci a una versione più grande, usa il rapporto  . Quando si ridimensiona una figura, utilizzare il rapporto
. Quando si ridimensiona una figura, utilizzare il rapporto  .
.
 . Quando si ridimensiona una figura, utilizzare il rapporto
. Quando si ridimensiona una figura, utilizzare il rapporto  .
. .
.Inserendo i valori corretti, questo diventa
 .
.
4. Semplifica il rapporto. Il rapporto semplificato, o frazione, fornisce il fattore di scala. Se riduci il fattore di scala sarà una frazione regolare. Se ingrandisci diventa un numero intero o una frazione impropria, che puoi convertire in decimale.
 può essere semplificato a
può essere semplificato a . Quindi il fattore di scala di due triangoli, uno con base di 15 cm e uno con base di 10 cm, è
. Quindi il fattore di scala di due triangoli, uno con base di 15 cm e uno con base di 10 cm, è  .
.Metodo 2 di 4: determinazione di una cifra corrispondente utilizzando il fattore di scala

1. Determina la lunghezza del lato della figura. Hai bisogno di una figura i cui lati siano dati o misurabili. Se non è possibile determinare la lunghezza del lato dell`immagine, non è possibile creare una figura in scala.
- Ad esempio: hai un triangolo rettangolo con i lati di 4 cm e 3 cm e un`ipotenusa di 5 cm.

2. Decidi se ingrandire o ridurre. Se ingrandisci, la cifra mancante aumenterà e il fattore di scala sarà un numero intero, una frazione impropria o un decimale. Man mano che ti rimpicciolisci, la cifra si riduce e il tuo fattore di scala è molto probabilmente una frazione regolare.

3. Moltiplica la lunghezza di un lato per il fattore di scala. Il fattore di scala deve essere indicato. Moltiplicando la lunghezza del lato per il fattore di scala si restituisce il lato mancante della figura in scala.
 . Quindi il triangolo scalato ha un`ipotenusa di 10 cm.
. Quindi il triangolo scalato ha un`ipotenusa di 10 cm.
4. Determina gli altri lati della figura. Continua a moltiplicare ogni lato per il fattore di scala. Questo ti darà i lati corrispondenti della figura mancante.
 per la base del triangolo scalato. Se l`altezza di un triangolo rettangolo è lungo 4 cm, con un fattore di scala di 2, allora calcola
per la base del triangolo scalato. Se l`altezza di un triangolo rettangolo è lungo 4 cm, con un fattore di scala di 2, allora calcola  per l`altezza del triangolo scalato.
per l`altezza del triangolo scalato.Metodo 3 di 4: Alcuni esempi di esercizi

1. Determina il fattore di scala di queste figure corrispondenti: un rettangolo con un`altezza di 6 cm e un rettangolo con un`altezza di 54 cm.
- Confronta le due altezze. Per aumentare, il rapporto è
. Per ridurre, usa il rapporto
.
- Semplifica il rapporto. Il rapporto
può essere semplificato a
. Il rapporto
può essere semplificato a
. Quindi i due rettangoli hanno un fattore di scala di
o
.

2. Prova la seguente attività. Un poligono irregolare è lungo 14 cm nel punto più largo. Un corrispondente poligono irregolare misura 8 cm nella parte più larga. Qual è il fattore di scala?
 . Se hai intenzione di ridurre, usa il rapporto
. Se hai intenzione di ridurre, usa il rapporto  .
. può essere semplificato a
può essere semplificato a  . Il rapporto
. Il rapporto  può essere semplificato a
può essere semplificato a  . Quindi i due poligoni irregolari hanno un fattore di scala di
. Quindi i due poligoni irregolari hanno un fattore di scala di  o
o  .
.
3. Utilizzare il fattore di scala per rispondere al seguente problema. Il rettangolo ABCD misura 8 cm x 3 cm. rettangolo EFGH è un rettangolo corrispondente più grande. Dato è un fattore di scala di 2,5. Qual è l`area del rettangolo EFGH?
 .
. .
. . Quindi, l`area del rettangolo EFGH è di 150 cm2.
. Quindi, l`area del rettangolo EFGH è di 150 cm2.Metodo 4 di 4: Il fattore di scala in chimica

1. Dividi la massa molare di una sostanza per quella della formula empirica. Quando conosci la formula empirica di un composto chimico e hai bisogno della formula molecolare della stessa sostanza chimica, puoi trovare il fattore di scala di cui hai bisogno dividendo la massa molare della sostanza per la massa molare della formula empirica.
- Ad esempio: vuoi conoscere la massa molare di un composto H2O con una massa molare di 54,05 g/mol.
- La massa molare di H2O è 18,0152 g/mol.
- Determina il fattore di scala dividendo la massa molare del composto per la massa molare della formula empirica:
- Fattore di scala = 54,05 / 18,0152 = 3

2. Moltiplica la formula empirica per il fattore di scala. Moltiplica il pedice di ogni elemento all`interno della formula empirica per il fattore di scala appena calcolato. Questo ti darà la formula molecolare del composto.

3. Scrivi la risposta. Con questa risposta hai trovato la risposta corretta per la formula empirica e per la formula molecolare del legame chimico.
Articoli sull'argomento "Determinazione del fattore di scala"
Condividi sui social network:
Simile
Popolare