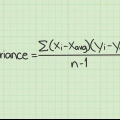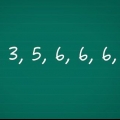Come Calcolare il Coefficiente di Correlazione del Rango di Spearman

Contenuto

Passi
Consigli
Avvertenze

Con il coefficiente di correlazione del rango di Spearman puoi vedere se due variabili sono correlate da una funzione monotona (d.w.z. che se un numero aumenta, aumenta anche l`altro numero o viceversa). Per calcolare il coefficiente di correlazione del rango di Spearman, devi ordinare e confrontare i set di dati per trovare Σd, quindi inserire quel valore nella versione standard o semplificata della formula del coefficiente di correlazione del rango di Spearman. Puoi anche calcolare questo coefficiente con formule di Excel o comandi R.

Passi

Metodo 1 di 3: manualmente

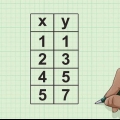
1. Disegna la tua tabella dati. Organizza le informazioni necessarie per calcolare il coefficiente di correlazione del rango di Spearman. Hai bisogno:

6 colonne di intestazioni, come mostrato sopra.
Tante righe quante sono le coppie di dati.

2. Riempi le prime due colonne con le tue coppie di dati.

3. Disporre i punti dati della prima colonna nella terza colonna, da 1 a n (il numero totale di punti dati che hai). Assegna al numero più basso la posizione 1, al numero successivo la posizione 2 e così via.

4. Fai lo stesso con la quarta colonna come nel passaggio 3, ma ora disponi la seconda colonna.

Se hai due (o più) punti dati con lo stesso valore in una colonna, prendi la media delle posizioni che quei punti dati avrebbero normalmente e assegna ai punti dati questa media come nuova posizione.
Nell`esempio a destra ci sono due cinque che normalmente sarebbero in posizione 2 e 3. Sono due le stesse canzoni, quindi prendi la media delle loro posizioni. La media di 2 e 3 è 2,5, quindi dai a entrambi i cinque la posizione 2,5.

5. Nella colonna `d`, calcola la differenza tra le due posizioni in ciascuna coppia di dati. In altre parole, se uno ha la posizione 1 e l`altro ha la posizione 3, la differenza è 2. (Positivo o negativo non importa, dal momento che raddozzeremo questa differenza nel passaggio successivo.)

6. Al quadrato i valori nella colonna d e scrivi questi valori nella colonna d.

7. Somma tutti i punti dati nella colonna d insieme. Questo valore è Σd.

8. Scegli una delle formule seguenti:

Se non si sono verificati punti dati uguali nei passaggi precedenti, immettere Σd nella formula semplice per il coefficiente di correlazione del rango di Spearman

e inserisci il numero di coppie di dati per `n` per trovare la tua risposta.

Se si sono verificati punti dati simili nei passaggi precedenti, utilizzare la formula standard per il coefficiente di correlazione del rango di Spearman:

9. Interpreta il risultato. Questo può variare tra -1 e 1.

Vicino a -1 – Correlazione negativa.

Vicino a 0 – Nessuna correlazione lineare.

Vicino a 1 – Correlazione positiva.

Metodo 2 di 3: In Excel

1. Crea nuove colonne con le posizioni delle colonne esistenti. Ad esempio, se hai i tuoi dati nella colonna A2:A11, utilizzerai la formula `=RANK(A2,A$2:A$11)` ed estenderai l`intervallo a tutte le righe e colonne.

2. Trattare punti dati uguali come descritto nei passaggi 3 e 4 del metodo 1.

3. In una nuova cella, esegui un calcolo di correlazione tra le due colonne con una formula come `=CORREL(C2:C11,D2:D11)`. In questo caso, C e D sono le colonne di posizione. Il coefficiente di correlazione del rango di Spearman appare nella cella di correlazione.

Metodo 3 di 3: Con R

1. Installa R se non lo hai già. (Vedere https://www.r-progetto.org/.)

2. Salva i tuoi dati come file CSV, con i dati che desideri correlare nelle prime due colonne. Puoi farlo con il menu "Salva con nome".

3. Apri l`editor R. Se stai lavorando nel terminale, esegui semplicemente R. Quando sei sul desktop, fai clic sul logo R.

4. Digita i seguenti comandi:

D <- leggere.csv("NAME_OF_YOU_CSV.csv") e premere invio

cor(rank(d[,1]),rank(d[,2]))

Consigli

La maggior parte dei set di dati richiede almeno cinque coppie di dati per stabilire una tendenza (nell`esempio sono state utilizzate solo tre coppie per semplificare l`esempio).

Avvertenze

Il coefficiente di correlazione del rango di Spearman mostra la forza di correlazione solo se i punti dati sono in continuo aumento o diminuzione. Se il grafico a dispersione dei punti dati mostra un andamento diverso, il coefficiente di correlazione del rango di Spearman aumenterà la correlazione non visualizzare correttamente.
Questa formula si basa sul presupposto che non esistono punti dati uguali. Se ci sono punti dati uguali, come nell`esempio precedente, utilizzare la seguente definizione: il coefficiente di correlazione momento-prodotto per i ranghi.