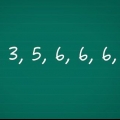Continuiamo a lavorare con l`esempio sopra. Ecco il nostro set di dati che mostra le temperature in gradi Fahrenheit di vari oggetti in una stanza: {71, 70, 73, 70, 70, 69, 70, 72, 71, 300, 71, 69}. Se ordiniamo i valori nell`insieme dal più basso al più alto, questo diventa il nostro nuovo insieme: {69, 69, 70, 70, 70, 70, 71, 71, 71, 72, 73, 300}. 
Non lasciarti confondere dai set di dati con un numero pari di punti - la media dei due punti centrali è spesso un numero che non è nel set di dati stesso - va bene. Tuttavia, se i due punti centrali sono gli stessi, la media sarà ovviamente anche questo numero - anche questo lo è Bene. Nel nostro esempio abbiamo 12 punti. I due termini centrali sono i punti 6 e 7 – 70 e 71. rispettivamente. Quindi la mediana del nostro set di dati è la media di questi due punti: ((70 + 71) / 2)=70.5. 
Nel nostro esempio, sei punti sono sopra la mediana e sei sotto di essa. Quindi per trovare il primo quartile dobbiamo prendere la media dei due punti centrali negli ultimi sei punti. I punti 3 e 4 degli ultimi sei sono entrambi 70, quindi la loro media è ((70 + 70) / 2)=70. Quindi il nostro valore per il Q1 è 70. 
Continuando con l`esempio sopra, vediamo che i due punti medi dei sei punti sopra la mediana sono 71 e 72. La media di questi due punti è ((71 + 72) / 2)=71.5. Quindi il nostro valore per il terzo trimestre è 71,5. 
Nel nostro esempio i valori per Q1 e Q3 sono rispettivamente 70 e 71,5. Per trovare l`intervallo interquartile, calcoliamo Q3 - Q1: 71,5 - 70=1,5. Funziona anche se Q1, Q3 o entrambi i numeri sono negativi. Ad esempio, se il nostro valore per Q1 fosse -70, l`intervallo interquartile sarebbe 71,5 - (-70)=141,5, che è corretto. 
Nel nostro esempio, l`intervallo interquartile è (71,5 - 70) o 1,5. Moltiplica questo per 1,5 e ottieni 2,25. Aggiungiamo questo numero a Q3 e lo sottraiamo da Q1, per trovare i limiti interni come segue: 71,5 + 2,25=73,75 70 - 2.25=67.75 Così sono i confini interni 67.75 e 73.75. Nel nostro set di dati, solo la temperatura del forno – 300 gradi Fahrenheit – è al di fuori di questo intervallo. Quindi questo potrebbe essere un lieve valore anomalo. Tuttavia, dobbiamo anche determinare se questa temperatura è un valore anomalo estremo, quindi non saltiamo ancora alle conclusioni.

Nel nostro esempio, moltiplichiamo l`intervallo interquartile per 3 e arriviamo a (1,5 * 3) o 4,5. Possiamo ora trovare i limiti esterni allo stesso modo dei limiti interni: 71,5 + 4,5=76 70 - 4,5=65,5 Quindi ci sono i limiti esterni 65.5 e 76. I punti dati che si trovano al di fuori dei confini esterni sono considerati valori anomali estremi. Nel nostro esempio, la temperatura del forno, 300 gradi Fahrenheit, è ben al di fuori dei limiti esterni. Quindi la temperatura del forno è sicuro un valore anomalo estremo.

Un altro criterio da considerare è se i valori anomali influiscono sulla media di un set di dati in modo distorto o fuorviante. Ciò è particolarmente importante se intendi trarre conclusioni dalla media del tuo set di dati. Esaminiamo il nostro esempio. Da quel momento altamente Sebbene sia improbabile che il forno abbia raggiunto una temperatura di 300°F a causa di una forza imprevista della natura, nel nostro esempio possiamo concludere con quasi il 100% di certezza che il forno è stato lasciato acceso accidentalmente, determinando una lettura di temperatura anormalmente elevata. Inoltre, se non rimuoviamo il valore anomalo, il nostro set di dati ha una media di (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73 + 300)/12=89,67 °F, mentre la media privo di il valore anomalo risulta a (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73)/11=70,55 °F. Poiché il valore anomalo è stato causato da un errore umano e poiché non è corretto dire che la temperatura ambiente media era prossima a 32°C, dobbiamo scegliere di scegliere il nostro valore anomalo rimuovere. 
Ad esempio, immagina di progettare un nuovo farmaco per far crescere i pesci in un allevamento ittico. Usiamo il nostro vecchio set di dati ({71, 70, 73, 70, 70, 69, 70, 72, 71, 300, 71, 69}), tranne per il fatto che ogni punto ora rappresenta la massa di un pesce (in grammi) dopo trattamento con un altro farmaco sperimentale dalla nascita. In altre parole, il primo farmaco dava a un pesce una massa di 71 grammi, il secondo dava a un altro pesce una massa di 70 grammi e così via. In questa situazione 300. è ancora un enorme valore anomalo, ma non dovremmo rimuoverlo ora. Perché, se assumiamo che il valore anomalo non sia il risultato di un errore, rappresenta un grande successo nel nostro esperimento. Il farmaco che ha prodotto un pesce da 300 grammi ha funzionato meglio di qualsiasi altro farmaco, quindi è così più punto dati importante nel nostro set, piuttosto che il meno punto dati importante.
Calcola valori anomali
UN anomalo o anomalo nelle statistiche, un punto dati che differisce significativamente dagli altri punti dati in un campione. Spesso i valori anomali segnalano agli statistici anomalie o errori nelle misurazioni, dopodiché possono rimuovere i valori anomali dal set di dati. Se effettivamente scelgono di rimuovere i valori anomali dal set di dati, ciò potrebbe apportare modifiche significative alle conclusioni tratte dallo studio. Questo è il motivo per cui è importante calcolare e determinare i valori anomali se si desidera interpretare correttamente i dati statistici.
Passi

1. Scopri come individuare potenziali valori anomali. Prima di poter decidere se rimuovere i valori anomali da un determinato set di dati, dobbiamo ovviamente riconoscere i possibili valori anomali nel set di dati. In generale, i valori anomali sono i punti dati che si discostano in modo significativo dalla tendenza che gli altri valori nella forma impostata – in altre parole, sparare degli altri valori. Di solito è facile riconoscerlo nelle tabelle e (soprattutto) nei grafici. Se il set di dati è rappresentato graficamente, i valori anomali saranno "lontani" dagli altri valori. Ad esempio, se la maggior parte dei punti in un set di dati forma una linea retta, i valori anomali non saranno conformi a questa linea.
- Diamo un`occhiata a un set di dati che mostra le temperature di 12 oggetti diversi in una stanza. Se la temperatura di 11 degli oggetti oscilla intorno ai 21°C al massimo di qualche grado, mentre un oggetto, un forno, ha una temperatura di 150°C, puoi vedere a colpo d`occhio che il forno è probabilmente un valore anomalo.

2. Ordina tutti i punti dati dal basso verso l`alto. Il primo passaggio nel calcolo dei valori anomali consiste nel trovare il valore mediano (o il valore medio) del set di dati. Questo compito diventa molto più semplice se i valori nel set sono in ordine dal più basso al più alto. Quindi, prima di continuare, ordina i valori nel tuo set di dati in questo modo.

3. Calcola la mediana del set di dati. La mediana di un set di dati è il punto dati in cui metà dei dati è al di sopra e metà dei dati è al di sotto: è fondamentalmente il "centro" del set di dati. Se il set di dati contiene un numero dispari di punti, la mediana è facile da trovare: la mediana è il punto con tanti punti sopra e sotto di essa. Se c`è un numero pari di punti, poiché non c`è un punto medio, devi prendere la media dei due punti medi per trovare la mediana. Quando si calcolano i valori anomali, la mediana è solitamente indicata dalla variabile Q2, poiché si trova tra Q1 e Q3, il primo e il terzo quartile. Determineremo queste variabili in seguito.

4. Calcola il primo quartile. Questo punto, che chiamiamo variabile Q1, è il punto dati al di sotto del quale si trova il 25 percento (o un quarto) delle osservazioni. In altre parole, questo è il punto medio di tutti i punti nel set di dati qui di seguito la mediana. Se c`è un numero pari di valori al di sotto della mediana, devi fare nuovamente la media dei due valori medi per trovare Q1, come potresti aver già fatto per determinare tu stesso la mediana.

5. Calcola il terzo quartile. Questo punto, che indichiamo con la variabile Q3, è il punto dati al di sopra del quale si trova il 25 percento dei dati. Trovare Q3 è praticamente come trovare Q1, tranne che in questo caso stiamo guardando i punti sopra la mediana.

6. Trova l`intervallo interquartile. Ora che abbiamo determinato Q1 e Q3 dobbiamo calcolare la distanza tra queste due variabili. La distanza tra Q1 e Q3 può essere trovata sottraendo Q1 da Q3. Il valore che ottieni per l`intervallo interquartile è fondamentale per determinare i limiti per i punti non devianti nel tuo set di dati.

7. Trova i "limiti interni" del set di dati. È possibile identificare i valori anomali determinando se rientrano in un certo numero di limiti numerici; i cosiddetti "valori limite interni" e "valori limite esterni". Un punto che non rientra nei limiti interni del set di dati è classificato come a lieve anomalia, e un punto che cade al di fuori dei limiti esterni è classificato come a estremo valore anomalo. Per trovare i limiti interni del tuo set di dati, moltiplica prima l`intervallo interquartile per 1,5. Aggiungi il risultato a Q3 e sottrailo da Q1. I due risultati sono i limiti interni del tuo set di dati.


8. Trova i "limiti esterni" del set di dati. Lo fai allo stesso modo dei limiti interni, con l`unica differenza che moltiplichi l`intervallo interquartile per 3 anziché per 1,5. Quindi aggiungi il risultato a Q3 e sottrai da Q1 per trovare i limiti esterni.


9. Utilizzare una valutazione qualitativa per determinare se è necessario "scartare" i valori anomali. Con il metodo sopra è possibile determinare se alcuni punti sono valori anomali lievi, valori anomali estremi o nessun valore anomalo. Ma non commettere errori: riconoscere un punto come anomalo lo rende solo uno candidato da rimuovere dal set di dati e non rimuovere immediatamente un punto dovere trasformarsi in. Il cavalcò il motivo per cui un valore anomalo è diverso dal resto dei punti dell`insieme è fondamentale per determinare se l`anomalia debba essere rimossa. In generale, i valori anomali causati da qualche errore - un errore nelle misurazioni, nelle registrazioni o nel disegno sperimentale, per esempio - vengono rimossi. Al contrario, di solito lo sono valori anomali che non sono causati da errori e che rivelano informazioni o tendenze nuove e impreviste non cancellato.

10. Comprendere l`importanza di (a volte) conservare i valori anomali. Mentre alcuni valori anomali dovrebbero essere rimossi da un set di dati perché sono il risultato di errori o perché distorcono in modo fuorviante i risultati, altri valori anomali dovrebbero essere mantenuti. Ad esempio, se un outlier è stato ottenuto correttamente (e quindi non è il risultato di un errore) e/o se l`outlier fornisce una nuova visione del fenomeno da misurare, non dovrebbe essere rimosso immediatamente. Gli esperimenti scientifici sono situazioni particolarmente delicate quando si tratta di trattare con valori anomali: rimuovere erroneamente un valore anomalo può significare scartare informazioni importanti su una nuova tendenza o scoperta.
Consigli
- Se trovi valori anomali, prova a spiegarli prima di rimuoverli dal set di dati; possono indicare errori di misurazione o deviazioni nella distribuzione.
Necessità
- Calcolatrice
Articoli sull'argomento "Calcola valori anomali"
Condividi sui social network:
Popolare