Esempio: `Numero di libri` in cima alla prima colonna. Scrivi "Frequenza" nella parte superiore della seconda colonna. Nella seconda riga, scrivi il primo valore in Numero di libri: 3. Conta il numero di tre nel tuo set di dati. Poiché ci sono due tre, digita 2 sotto frequenza nella stessa riga. Ripetere per ogni valore fino a completare l`intera tabella: 3 | F=2 5 | F=1 6 | F=3 8 | F=1 
Esempio: Il valore più basso è tre. Il numero di studenti che hanno letto tre libri è due. Nessuno ha letto meno libri, quindi la frequenza cumulativa è tre. Aggiungi questo alla prima riga della tabella: 3 | F=2 | CF=2 
Esempio: 3 | F=2 | CF=2 5 | F=1 | CF=2+1=3 
Esempio: 3 | F=2 | CF=2 5 | F=1 | CF=2 + 1=3 6 | F=3 | CF=3 + 3=6 8 | F=1 | CF=6 + 1=7 
Somma le singole frequenze: 2 + 1 + 3 + 1=7, la nostra ultima frequenza cumulativa. Conta il numero di punti dati. La nostra lista era 3, 3, 5, 6, 6, 6, 8. Ci sono sette oggetti, la nostra frequenza cumulativa finale. 

Set di dati: 233, 259, 277, 278, 289, 301, 303 Tabella (prima colonna -- valore, seconda colonna -- frequenza, terza colonna -- frequenza cumulativa): 200–250|1|1 251–300|4|1 + 4=5 301–350|2|5 + 2=7 
Ad esempio: se il tuo set di dati va da 1 a 8, disegna un asse x con otto unità contrassegnate su di esso. Su ciascun valore dell`asse x, traccia un punto sul valore y che è uguale alla frequenza cumulativa in quel punto. Collega ogni coppia di punti adiacenti con una linea. Se non ci sono punti dati in un dato valore, la frequenza assoluta è zero. L`aggiunta di zero all`ultima frequenza cumulativa non cambierà il valore, quindi disegniamo un punto allo stesso valore y dell`ultimo valore. Poiché la frequenza cumulativa aumenta sempre insieme ai valori, il grafico dovrebbe sempre rimanere stabile o salire mentre si sposta verso destra. Se la linea scende ad un certo punto, potresti guardare accidentalmente una frequenza assoluta. 
Osserva l`ultimo punto sul lato destro del grafico. Il valore y è la frequenza cumulativa totale, che è il numero di punti nel set di dati. Supponiamo che questo valore sia uguale a 16. Moltiplica questo valore per ½ e trovalo sull`asse y. Nel nostro esempio, questo è 8 (metà di 16). Trova 8 sull`asse y. Trova il punto sul grafico a questo valore y. Sposta il dito dall`8 sull`asse y lungo il grafico. Fermati quando il dito tocca la linea del grafico. Questo è il punto in cui viene conteggiata esattamente la metà dei tuoi punti dati. Determina il valore x a questo punto. Sposta il dito verso il basso sull`asse x. Questo valore è la mediana del tuo set di dati. Ad esempio, se questo valore è 65, metà del tuo set di dati è inferiore a 65 e metà è superiore a 65. 
Per trovare il valore y del quartile inferiore, prendi la frequenza cumulativa massima e moltiplicala per ¼. Il valore x corrispondente ti darà il valore y, con esattamente un quarto dei dati sotto di esso. Per trovare il valore y del quartile superiore, moltiplicare la frequenza cumulativa massima per ¾. Il valore x corrispondente ti darà il valore y, con esattamente tre quarti dei dati sotto e un quarto sopra.
Calcola frequenza cumulativa
Contenuto
Nelle statistiche, la frequenza assoluta si riferisce al numero di volte in cui un dato valore viene visualizzato in un set di dati. La frequenza cumulativa è diversa: è la somma (o totale preliminare) di tutte le frequenze fino al punto corrente nel set di dati. Non preoccuparti se suona come un gergo; è facile se prendi carta e penna.
Passi
Parte 1 di 2: Determinazione della frequenza cumulativa fondamentale

1. Ordina il set di dati. Un "set di dati" è solo il gruppo di numeri che stai studiando. Ordina questi valori dal più piccolo al più grande.
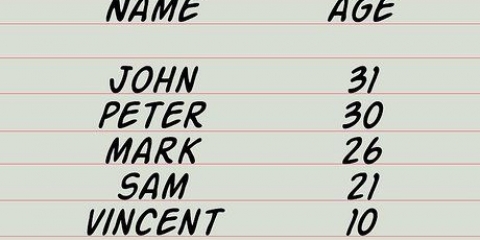
- Esempio: Il tuo set di dati contiene il numero di libri che ogni studente ha letto nell`ultimo mese. Dopo l`ordinamento, questo è il set di dati: 3, 3, 5, 6, 6, 6, 8.

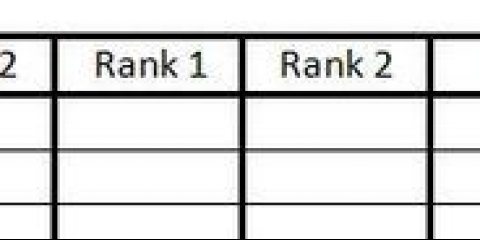
2. Conta la frequenza assoluta di ogni valore. La frequenza di un valore è il numero di volte in cui il valore viene visualizzato (puoi chiamarlo "frequenza assoluta" se vuoi evitare confusione con la frequenza cumulativa). Il modo più semplice per tenerne traccia è creare una tabella. Digita "Valore" (o una descrizione di ciò che il valore misura) all`inizio della prima colonna. Scrivi "Frequenza" nella parte superiore della seconda colonna. Compila la tabella per ogni valore.

3. Determina la frequenza cumulativa del primo valore. La frequenza cumulativa risponde alla domanda "quante volte arriva questo valore? o un valore inferiore per?Inizia sempre con il valore più basso nel tuo set di dati. Poiché non ci sono valori più piccoli, la risposta è la stessa della frequenza assoluta di quel valore.

4. Determina la frequenza cumulativa del valore seguente. Passa al valore successivo nella tabella. Abbiamo appena scoperto quante volte si verificano i valori più bassi. Per determinare la frequenza cumulativa di questo valore, basta sommare la frequenza assoluta al totale parziale. In altre parole, prendi l`ultima frequenza cumulativa che hai trovato e aggiungi la frequenza assoluta di questo valore.

5. Ripetere per gli altri valori. Continua con valori sempre più grandi. Ogni volta, aggiungi l`ultima frequenza cumulativa alla frequenza assoluta del valore successivo.

6. Controlla il tuo lavoro. Una volta terminato, hai sommato il numero di istanze di ciascuna variabile. L`ultima frequenza cumulativa deve essere uguale al numero totale di punti dati nella serie. Ci sono due modi per verificarlo:
Parte 2 di 2: Fare di più con i dati

1. Comprendere dati discreti e continui. I dati discreti vengono forniti in unità che puoi contare, dove è impossibile determinare una parte di un`unità. I dati continui descrivono qualcosa che non può essere contato, con misurazioni che possono rientrare da qualche parte tra le unità che hai scelto. Ecco alcuni esempi:
- Numero di cani: Discreto. Non esiste un mezzo cane.
- Altezza neve: continua. La neve si accumula gradualmente, non in un`unità alla volta. Se hai provato a misurarlo in centimetri, potresti aver trovato uno strato di neve profondo 5,6 centimetri.

2. Raggruppa i dati continui per intervallo. I set di dati continui hanno spesso un numero elevato di variabili univoche. Cercare di utilizzare il metodo sopra renderebbe la tabella molto lunga e difficile da capire. Invece, rendi ogni riga della tua tabella un intervallo di valori. È importante che ogni intervallo abbia la stessa dimensione (come 0-10, 11– 20, 21-30, ecc.), indipendentemente dal numero di valori presenti in ciascun intervallo. Ecco un esempio di un set di dati continuo trasformato in una tabella:

3. Crea un grafico. Dopo aver calcolato la frequenza cumulativa, prendi della carta millimetrata. Disegna un grafico in cui l`asse x è uguale ai valori del tuo set di dati e l`asse y è uguale alla frequenza cumulativa. Ciò renderà i seguenti calcoli molto più semplici.

4. Trova la mediana del grafico. La mediana è il valore che si trova esattamente nel mezzo del set di dati. La metà dei valori è al di sopra della mediana e l`altra metà al di sotto di essa. Ecco come trovare la mediana nel grafico:

5. Determina i quartili dal grafico. I quartili dividono i dati in quattro sezioni. Questo processo è molto simile alla determinazione della mediana. L`unica differenza è come determini i valori y:
Consigli
- È possibile visualizzare qualsiasi set di dati di grandi dimensioni in intervalli, anche se i dati sono discreti.
Articoli sull'argomento "Calcola frequenza cumulativa"
Condividi sui social network:
Popolare