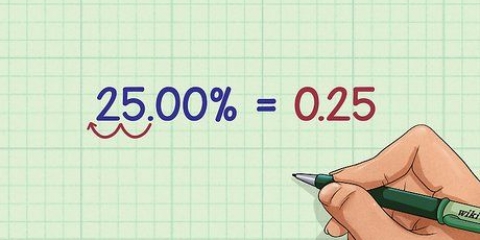Esempio 1: Qual è la probabilità di scegliere un giorno che cade in un fine settimana se viene selezionato un giorno della settimana casuale? Il numero di eventi è due (perché due giorni della settimana cadono nel fine settimana) e il numero di risultati è sette. La probabilità è 2 ÷ 7=2/7 o .285 o 28.5%. Esempio 2: Una bottiglia contiene 4 biglie blu, 5 biglie rosse e 11 biglie bianche. Se una biglia viene prelevata a caso dalla bottiglia, qual è la probabilità che questa biglia sia rossa?? Il numero di eventi è cinque (perché ci sono cinque biglie in totale) e il numero di risultati è 20. La probabilità è 5 ÷ 20=1/4 o 0,25 o 25%. 
Esempio 2:Due carte vengono estratte a caso da un mazzo di carte. Qual è la probabilità che entrambe le carte siano fiori?? La probabilità che la prima carta sia un club è 13/52, o 1/4 (ci sono 13 fiori in ogni seme). Ora sappiamo che la probabilità è 12/51 che la seconda carta sia un trifoglio. Sei tu a determinare la possibilità di eventi dipendenti. Questo perché ciò che fai la prima volta influisce sulla seconda; Se peschi un 3 fiori e non lo rimetti, c`è una carta e anche una fiori in meno nel seme (51 invece di 52). Esempio 3: Una bottiglia contiene 4 biglie blu, 5 biglie rosse e 11 biglie bianche. Se si prelevano a caso tre biglie dalla bottiglia, qual è la probabilità che la prima biglia sia rossa, la seconda biglia sia blu e la terza sia bianca? La probabilità che la prima biglia sia rossa è 5/20, o 1/4. La probabilità che la seconda biglia sia blu è 4/19, perché c`è una biglia in meno, ma non meno biglie blu. E la probabilità che la terza biglia sia bianca è 11/18, perché prima abbiamo scelto due biglie. Questa è un`altra disposizione dell`a evento indipendente. 
Esempio 1:Qual è la probabilità di tirare due volte un cinque con un dado regolare?? La probabilità di entrambi gli eventi indipendenti è 1/6. Questo ci dà: 1/6 x 1/6=1/36 o 0,027 o 2,7%. Esempio 2: Due carte vengono estratte a caso da un mazzo di carte. Qual è la probabilità che entrambe le carte siano fiori?? La probabilità del primo evento è 13/52. La probabilità del secondo evento è 12/51. La probabilità è 13/52 x 12/51=12/204 o 1/17 o 5,8%. Esempio 3: Una bottiglia contiene 4 biglie blu, 5 biglie rosse e 11 biglie bianche. Se si prelevano a caso tre biglie da una bottiglia, qual è la probabilità che la prima biglia sia rossa, la seconda biglia sia blu e la terza sia bianca? La probabilità del primo evento è 5/20. La probabilità del secondo evento è 4/19. E la probabilità del terzo evento è 18/11. La probabilità è 5/20 x 4/19 x 11/18=44/1368 o 3,2%. 

L`evento che il giocatore vincerà è 9; l`evento che il giocatore perde è 4. la somma dei pro e dei contro è 9 + 4, ovvero 13. Il calcolo è ora lo stesso del calcolo della probabilità di un singolo evento. 9 13=0,692 o 69,2%. Quindi la probabilità che il giocatore vinca è: 9/13. 


La probabilità di ottenere un tre con un dado regolare è 1/6. Questo ovviamente vale anche per gli altri numeri, e da questo segue: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6=6/6 o 1 o 100%. 
Calcola la probabilità
Contenuto
La probabilità è il grado di probabilità che un particolare evento si verifichi per un numero di possibili risultati. La probabilità ti dà la capacità di affrontare un problema con la logica, anche se c`è un certo grado di incertezza. Scopri come utilizzare le abilità matematiche comuni per calcolare le probabilità qui.
Passi
Parte 1 di 4: Probabilità di un singolo evento casuale

1. Determina l`evento e i possibili risultati. La probabilità è la probabilità che si verifichi un particolare evento divisa per il numero di possibili esiti. Quindi supponiamo di voler calcolare la probabilità di ottenere un tre, con un dado regolare. "lancia un tre" è l`evento, e poiché sappiamo che un dado regolare con 6 facce ha la stessa probabilità di atterrare su ogni lato, il numero di risultati è 6. Ecco altri due esempi per iniziare: Esempio 2: Una bottiglia contiene 4 biglie blu, 5 biglie rosse e 11 biglie bianche. Se una biglia viene prelevata a caso dalla bottiglia, qual è la probabilità che sia rossa?? "La scelta di un marmo rosso" è il nostro evento, e il numero di risultati è il numero totale di biglie nella bottiglia, 20.
- Esempio 1: Qual è la probabilità che tu scelga un giorno che cade in un fine settimana se scegli un giorno della settimana??
- "Scegliere un giorno che cade nel fine settimana" è il nostro evento e il numero di risultati è il numero totale di giorni della settimana.

2. Dividi il numero di eventi per il numero di possibili risultati. Questo ci dà la probabilità che si verifichi un singolo evento. Nel caso di un tre con un dado, il numero di eventi è 1 (c`è solo un 3 su un dado regolare) e il numero di risultati è sei. Puoi anche visualizzarlo come: 1 ÷ 6, 1/6, .166 o 16.6%. Ecco come trovare le quote per il resto dell`esempio:
Parte 2 di 4: Calcolo della probabilità di più eventi casuali
1. Rompi il problema in pezzi gestibili. Calcolare la probabilità di più eventi equivale a dividere il problema in "probabilità separate". Ecco tre esempi:

- Esempio 1:Qual è la probabilità di ottenere due volte cinque con un dado regolare a sei facce??
- Sai che la probabilità di tirare un cinque è 1/6, e anche la probabilità di tirare altri cinque con lo stesso dado è 1/6.
- Questi sono `eventi indipendenti`, perché ciò che lanci la prima volta non ha effetto sull`esito del secondo tiro; è possibile che tiri un 3 e altri tre.

2. Moltiplica la probabilità di ogni evento. Il risultato fornisce la probabilità che più eventi si verifichino uno dopo l`altro. Ecco cosa puoi fare:
Parte 3 di 4: Convertire le probabilità in caso

1. Determina quali sono le probabilità (l`odds ratio). Ad esempio, un giocatore di golf è il favorito per vincere con una possibilità di 9/4. Le probabilità di un evento sono il rapporto tra la probabilità che qualcosa accada e la probabilità che non accada.
- Nell`esempio del rapporto 9:4, 9 rappresenta la probabilità che il giocatore vinca. 4 rappresenta la probabilità che ciò non accada. Quindi questo rapporto mostra che il giocatore ha più probabilità di vincere che di perdere.
- Ricorda che quando scommetti negli sport e dai bookmaker, le quote sono espresse come "probabilità contro," il che significa che la probabilità che un evento non si verifichi viene scritta prima e la probabilità che un evento si verifichi in seguito. Anche se questo può creare confusione, è bene esserne consapevoli. In questo articolo non ci addentreremo ulteriormente "probabilità contro".

2. Converti le probabilità in caso. La conversione delle quote è abbastanza facile. Dividi le quote in due eventi separati che si sommano per dare le quote.
Parte 4 di 4: Le regole della probabilità

1. Assicurati che due eventi o risultati si escludano a vicenda. Ciò significa che non possono agire entrambi contemporaneamente.

2. Il caso non può essere negativo. Se i tuoi calcoli mostrano un numero negativo, controlla cosa hai fatto.

3. La probabilità di tutti i possibili eventi deve essere 1 su 100%. Se la probabilità di tutti i possibili eventi non soddisfa questo, hai commesso un errore da qualche parte, perché hai trascurato un possibile evento.

4. Rappresenta la probabilità di un risultato impossibile con uno 0. Ciò significa che non vi è alcuna possibilità che l`evento abbia luogo.
Articoli sull'argomento "Calcola la probabilità"
Condividi sui social network:
Popolare