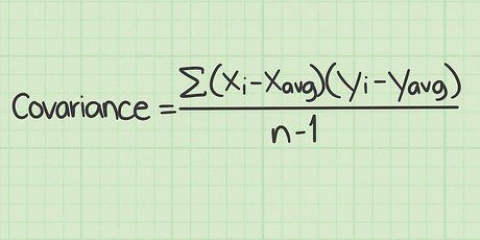La media è il valore medio di tutti i numeri. Calcoli la media sommando tutti i numeri nel tuo campione e poi dividendo questo valore per il numero di numeri nel tuo campione (n). Il set di dati del voto del test (10, 8, 10, 8, 8 e 4) è composto da 6 numeri. Vale quindi: n = 6. 
Ad esempio, utilizzare il set di dati del voto del test: 10, 8, 10, 8, 8 e 4. 10 + 8 + 10 + 8 + 8 + 4 = 48. Questa è la somma di tutti i numeri nel set di dati o nel campione. Aggiungi i numeri una seconda volta per verificare la risposta. 
Il set di dati del voto del test (10, 8, 10, 8, 8 e 4) è composto da sei numeri. Vale quindi: n = 6. La somma di tutti i voti dei test nell`esempio era 48. Quindi devi dividere 48 per n per calcolare la media. 48 / 6 = 8 Il voto medio del test nel campione è 8. 

Ad esempio, nel nostro campione di voti del test (10, 8, 10, 8, 8 e 4), la media o la media aritmetica era 8. 10 - 8 = 2; 8 - 8 = 0,10 - 8 = 2,8 - 8 = 0,8 - 8 = 0 e 4 - 8 = -4. Ripetere i calcoli per controllare ogni risposta. È molto importante che tutti i numeri siano corretti perché ne avrai bisogno per il passaggio successivo. 
Ricordiamo come nel nostro campione abbiamo sottratto la media (8) da ciascuno dei numeri nel campione (10, 8, 10, 8, 8 e 4) e abbiamo ottenuto i seguenti risultati: 2, 0, 2, 0 , 0 e -4. Nel calcolo seguente per determinare la varianza, procedi come segue: 2, 0, 2, 0, 0 e (-4) = 4, 0, 4, 0, 0 e 16. Si prega di controllare le risposte prima di passare al passaggio successivo. 
Nel nostro esempio del voto del test, abbiamo calcolato i seguenti quadrati: 4, 0, 4, 0, 0 e 16. Ricorda che nell`esempio abbiamo iniziato con i voti del test sottraendo la media di ciascuno dei numeri e poi quadrando i risultati: (10-8) + (8-8) + (10-2) + (8- 8) + ( 8-8) + (4-8) 4 + 0 + 4 + 0 + 0 + 16 = 24. La somma dei quadrati è 24. 
Il nostro campione di voti dei test (10, 8, 10, 8, 8 e 4) è composto da 6 cifre. Vale quindi: n = 6. n - 1 = 5. La somma dei quadrati per questo campione era 24. 24 / 5 = 4,8. Quindi la varianza di questo campione è 4,8. 

In genere almeno il 68% di tutti i valori rientra in una deviazione standard della media. Ricorda, nel nostro campione di voti dei test, la varianza era 4,8. √4,8 = 2,19. Quindi la deviazione standard del nostro campione di voti dei test è 2,19. 5 numeri su 6 (83%) nel nostro campione di voti del test (10, 8, 10, 8, 8 e 4) rientrano in una deviazione standard (2,19) dalla media (8). 
È importante scrivere tutti i passaggi quando si eseguono i calcoli a memoria o con una calcolatrice. Se ottieni un risultato diverso la seconda volta, controlla il tuo calcolo. Se non riesci a trovare l`errore, ricomincia da capo una terza volta per confrontare i tuoi calcoli.
Calcola la deviazione standard
Contenuto
La deviazione standard ti dice qual è lo spread dei numeri nel tuo campione. Per trovare la deviazione standard per il tuo campione o set di dati, devi prima eseguire alcuni calcoli. È necessario determinare la media e la varianza dei dati prima di poter calcolare la deviazione standard. La varianza è una misura della diffusione dei tuoi valori attorno alla media. La deviazione standard è determinata calcolando la radice quadrata della varianza.Questo articolo spiega come calcolare la media, la varianza e la deviazione standard.
Passi
Metodo 1 di 3: Calcola la media

1. Guarda la tua raccolta di dati. Questo è un passaggio importante in qualsiasi calcolo statistico, anche un semplice valore come la media o la mediana.
- Scopri quanti numeri contiene il tuo campione.
- I numeri sono distanti?? Oppure le differenze tra i numeri sono piccole, ad esempio solo poche cifre decimali?
- Scopri che tipo di dati stai guardando. Cosa significano i numeri nel tuo campione? Questo può essere, ad esempio, gradi di test, valori di frequenza cardiaca, altezza, peso e così via.
- Ad esempio, un set di dati del voto del test è costituito dai numeri 10, 8, 10, 8, 8 e 4.

2. Raccogli tutti i tuoi dati. Hai bisogno di ogni numero nel tuo campione per calcolare la media.

3. Somma i numeri nel tuo campione insieme. Questo è il primo passo nel calcolo della media aritmetica, o media.

4. Dividi la somma per il numero di numeri nel tuo campione (n). Calcola la media di tutti i dati.
Metodo 2 di 3: Trovare la varianza nel tuo campione

1. Determina la varianza. La varianza è un numero che indica la diffusione dei tuoi valori attorno alla media.
- Questo numero ti darà un`idea di quanto i valori differiscono l`uno dall`altro.
- I campioni a bassa varianza contengono valori che differiscono poco dalla media.
- I campioni ad alta varianza contengono valori che deviano molto dalla media.
- La varianza viene spesso utilizzata per confrontare la diffusione dei valori in due set di dati.

2. Sottrai la media di ciascuno dei numeri nel tuo campione. Ora ottieni una serie di valori che indicano quanto ogni numero nel campione differisce dalla media.

3. Al quadrato tutti i numeri che hai calcolato nel passaggio precedente. Hai bisogno di tutti questi valori per determinare la varianza del tuo campione.

4. Somma i numeri al quadrato. Questa è la somma dei quadrati.

5. Dividi la somma dei quadrati per (n-1). Ricorda che n rappresenta il numero di numeri nel campione. Eseguendo questo passaggio si determina la varianza.
Metodo 3 di 3: calcolo della deviazione standard

1. Nota la varianza. Hai bisogno di questo valore per calcolare la deviazione standard del tuo campione.
- Ricorda che la varianza è quanto i valori si discostano dalla media.
- La deviazione standard è un valore simile che indica la diffusione dei numeri nel campione.
- Nel nostro esempio dei voti del test, la varianza era 4,8.

2. Calcola la radice quadrata della varianza. Il risultato di questo è la deviazione standard.

3. Calcolare nuovamente la media, la varianza e la deviazione standard. Come controllare la tua risposta.
Articoli sull'argomento "Calcola la deviazione standard"
Condividi sui social network:
Popolare