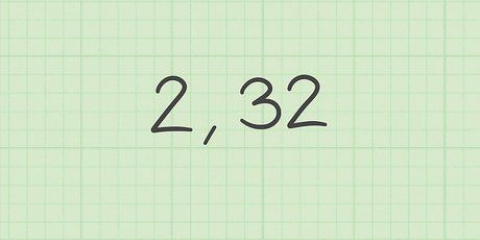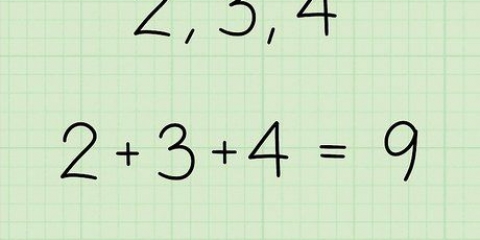Nell`esempio di raccolta dati, queste varianze diventano: 







Per verificare la validità dei tuoi calcoli, controlliamo se la somma dei valori nella colonna degli scostamenti è uguale a zero. Se sommi tutte le deviazioni e ottieni qualcosa di diverso da zero, la tua media non è corretta o hai commesso un errore nel calcolo di una o più deviazioni. Restituisci e controlla il tuo lavoro. 
Il valore assoluto è uno strumento matematico per indicare la distanza o la magnitudine, indipendentemente dalla direzione. Per determinare il valore assoluto, ometti semplicemente il segno meno per ogni numero nella seconda colonna. Quindi riempi la terza colonna con i valori assoluti come segue: 









Per questo set di dati, il calcolo finale sarà: 

Ad esempio, con questo set di dati, puoi dire che la media è nove e la distanza media dalla media è 2,75. Si noti che alcuni valori sono più vicini di 2,75 rispetto ad altri. Ma 2,75 è la distanza media.
Calcolo della deviazione media dalla media
Contenuto
Quando si lavora con i dati, ci sono diversi modi per misurare quanto strettamente sono raggruppati i valori dei dati. Il più comune è la media. La maggior parte delle persone impara a calcolare la media all`inizio della scuola trovando la somma di un gruppo di valori di dati e poi dividendo per il numero di valori nel gruppo. Un calcolo più avanzato è la deviazione media sulla media. Questo calcolo ti dice quanto sono vicini i tuoi valori alla media. Lo determini trovando la media di un set di dati, quindi la deviazione di ciascun dato da quella media e quindi la media di tali deviazioni.
Passi
Parte 1 di 2: Calcolo della media

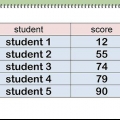
1. Raccogli e conta i tuoi dati. Per qualsiasi insieme di valori, la media è una misura del valore centrale. A seconda del tipo di dati, la media ti darà il valore medio di quei dati. Per trovare la media, devi prima raccogliere i tuoi dati, attraverso un esperimento o semplicemente affidandoli a un incarico.
- Come esempio usiamo una data sequenza numerica 6, 7, 10, 12, 13, 4, 8 e 12. Questa sequenza è abbastanza piccola da poter contare a mano e vedere subito che è una sequenza di otto numeri.
- All`interno della statistica, la variabile
o
spesso usato per indicare il numero di valori in una serie o collezione.

2. Trova la somma dei valori. Il primo passo per determinare la media è calcolare la somma di tutti i valori. All`interno della notazione statistica, ogni valore è generalmente rappresentato dalla variabile  . Alla somma di tutti i valori viene assegnato il simbolo
. Alla somma di tutti i valori viene assegnato il simbolo  . La lettera maiuscola greca sigma indica che è la somma dei valori. Il calcolo per questa semplice serie va così:
. La lettera maiuscola greca sigma indica che è la somma dei valori. Il calcolo per questa semplice serie va così:
 . Alla somma di tutti i valori viene assegnato il simbolo
. Alla somma di tutti i valori viene assegnato il simbolo  . La lettera maiuscola greca sigma indica che è la somma dei valori. Il calcolo per questa semplice serie va così:
. La lettera maiuscola greca sigma indica che è la somma dei valori. Il calcolo per questa semplice serie va così:

3. Condividi per trovare la media. Infine, dividi la somma per il numero di valori. La lettera greca mu,  , è spesso usato per indicare la media. Il calcolo della media procede quindi come segue:
, è spesso usato per indicare la media. Il calcolo della media procede quindi come segue:
 , è spesso usato per indicare la media. Il calcolo della media procede quindi come segue:
, è spesso usato per indicare la media. Il calcolo della media procede quindi come segue:
Parte 2 di 2: Determinazione della deviazione media

1. Crea una tabella. Per mantenere i tuoi dati in ordine e per facilitare i calcoli, è utile creare una tabella di tre colonne. Etichetta la prima colonna  . Etichetta la seconda colonna
. Etichetta la seconda colonna  . Etichetta la terza colonna
. Etichetta la terza colonna  .
.
 . Etichetta la seconda colonna
. Etichetta la seconda colonna  . Etichetta la terza colonna
. Etichetta la terza colonna  .
. - Riempi la prima colonna con i valori per il tuo calcolo.

2. Calcola la deviazione (deviazione) di ciascun valore. Nella seconda colonna, etichettata  , inserisci la deviazione o la differenza tra ciascun valore e la media della serie o dell`insieme. Trova questo valore sottraendo la media da ogni valore di dati.
, inserisci la deviazione o la differenza tra ciascun valore e la media della serie o dell`insieme. Trova questo valore sottraendo la media da ogni valore di dati.
 , inserisci la deviazione o la differenza tra ciascun valore e la media della serie o dell`insieme. Trova questo valore sottraendo la media da ogni valore di dati.
, inserisci la deviazione o la differenza tra ciascun valore e la media della serie o dell`insieme. Trova questo valore sottraendo la media da ogni valore di dati.








3. Determina il valore assoluto di ogni deviazione. Quando calcoli la deviazione di qualsiasi valore dalla media, vuoi solo conoscere la differenza, non se quella differenza è positiva o negativa. Ciò di cui hai veramente bisogno, in termini matematici, è il valore assoluto della differenza. Il valore assoluto è indicato da barre verticali| |.










4. Calcola la media delle deviazioni assolute. Dopo aver completato la tabella a tre colonne, trova la media dei valori assoluti nella terza colonna. Proprio come hai fatto per calcolare la media dei valori iniziali, somma le deviazioni e dividi la somma per il numero di valori.


5. Interpreta il risultato. Il valore della deviazione media dalla media è una misura di quanto vicini sono i valori tra loro. Questo risponde alla domanda "Quanto sono vicini alla media i valori dei dati in media?"?`
Consigli
- Continua a esercitarti e sarai in grado di calcolarlo senza problemi.
Articoli sull'argomento "Calcolo della deviazione media dalla media"
Condividi sui social network:
Simile
Popolare