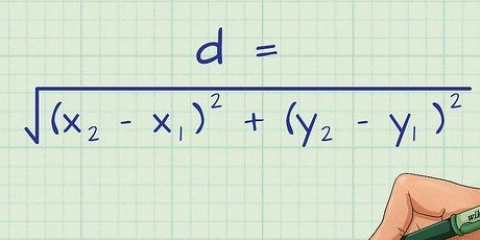Calcolo della media e della deviazione standard

1. Raccogli una serie di numeri che desideri analizzare. Questi dati sono indicati come campione.

• Ad esempio, un test è stato somministrato a una classe di 5 studenti e i risultati del test sono 12, 55, 74, 79 e 90.
  
  

Metodo 2 di 4: La media

1. Calcola la media. Somma tutti i numeri e dividi per la popolazione:

• Media (μ) = ΣX/N, dove Σ è il segno di somma (addizione), x_io qualsiasi numero nella serie e N è la dimensione della popolazione.
  
  
• Nel caso precedente, la media μ è semplicemente (12+55+74+79+90)/5 = 62.
  
  

Metodo 3 di 4: La deviazione standard

1. Calcola la deviazione standard. Questo rappresenta la distribuzione della popolazione. Deviazione standard= σ = sq rt [(Σ((X-μ)^2))/(N)].

• Nell`esempio fornito, la deviazione standard è: sqrt[((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62) ^2 )/(5)] = 27.4 (Nota che nel caso della deviazione standard di un campione, dividi per n-1, la dimensione del campione meno 1).
  
  

Metodo 4 di 4: L`errore standard della media

1. Calcola l`errore standard (dalla media). Ciò indica quanto la media campionaria si avvicini alla media della popolazione. Più grande è il campione, minore è l`errore standard e più vicina è la media del campione alla media della popolazione. Puoi farlo dividendo la deviazione standard per la radice quadrata N, la dimensione del campione. L`errore standard è = σ/sqrt(n).

• Quindi per quanto riguarda l`esempio sopra, se questo era un campione di 5 studenti di una classe di 50, e i 50 studenti hanno una deviazione standard di(σ = 21), allora l`errore standard = 17/sqrt(5) = 7.6.
  
  

Consigli

• Il calcolo della media, della mediana, della deviazione standard e dell`errore standard è molto utile per l`analisi della distribuzione normale dei dati. Una deviazione standard su una misura del centro occupa circa il 68% dei dati, 2 deviazioni standard il 95% e 3 deviazioni standard 99.7 per cento. L`errore standard si riduce (diffusione più stretta) man mano che il campione aumenta.
• Una calcolatrice facile da usare per il calcolo della deviazione standard

Avvertenze

• Controlla attentamente i tuoi calcoli. È molto facile commettere errori o inserire numeri in modo errato qui.