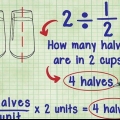Dividendo un intero per una frazione

Contenuto

Se vuoi dividere un numero intero per una frazione, in realtà calcoli quanti "gruppi" della frazione vanno nell`intero. Il modo standard per dividere un numero intero per una frazione è moltiplicare il numero intero per il reciproco della frazione. Puoi anche creare un grafico per aiutare a visualizzare questo calcolo.

Passi

Metodo 1 di 3: Moltiplica per l`inverso

Immagine titolata Dividi un numero intero con una frazione Passaggio 1
1. Converti il ​​numero intero in una frazione. Puoi farlo trasformando l`intero numero nel numeratore di una frazione. Crea il denominatore 1.
  • Ad esempio: calcola il tuo 7÷34{displaystyle 7div {frac {3}{4}}}{displaystyle 7div {frac {3}{4}}}, poi tu cambi prima 7{ displaystyle 7}7 in 71{displaystyle {frac {7}{1}}}{displaystyle {frac {7}{1}}}.
Immagine titolata Dividi un numero intero con una frazione Step 2
2. Trova il reciproco della frazione. Il reciproco di un numero è uguale all`inverso di quel numero. Per trovare il reciproco di una frazione, scambia il numeratore e il denominatore.
  • Ad esempio: l`inverso (l`inverso) di 34{displaystyle {frac {3}{4}}}{frac{3}{4}} è 43{displaystyle {frac {4}{3}}}{displaystyle {frac {4}{3}}}.
    • Immagine titolata Dividi un numero intero con una frazione Step 3
    3. Moltiplica le due frazioni. Per moltiplicare le frazioni, prima moltiplicare insieme i numeratori. Quindi moltiplica i denominatori insieme. Il prodotto delle due frazioni è uguale al quoziente del tuo problema di divisione originale.
  • Ad esempio: 71×43=283{displaystyle {frac {7}{1}}times {frac {4}{3}}={frac {28}{3}}}{displaystyle {frac {7}{1}}times {frac {4}{3}}={frac {28}{3}}}
    • Immagine titolata Dividi un numero intero per una frazione Step 4
    4. Semplificare, se necessario. Se hai una frazione impropria (cioè il numeratore è maggiore del denominatore), il problema potrebbe chiederti di cambiarla in un numero misto. Normalmente, la dichiarazione chiederà per semplificare le frazioni ai minimi termini.
  • Ad esempio: 283{displaystyle {frac {28}{3}}}{displaystyle {frac {28}{3}}} può essere semplificato al numero misto 913{displaystyle 9{frac {1}{3}}}{displaystyle 9{frac {1}{3}}}.

    • Metodo 2 di 3: tracciare un diagramma

    Immagine titolata Dividi un numero intero con una frazione Step 5
    1. Disegna forme che rappresentano il numero intero. La tua forma deve poter essere divisa in gruppi uguali, come un quadrato o un cerchio. Disegna le forme così grandi da poterle dividere in pezzi più piccoli.
    • Ad esempio: nel calcolo 5÷34{displaystyle 5div {frac {3}{4}}}{displaystyle 5div {frac {3}{4}}}, disegneresti cinque cerchi.
    Immagine titolata Dividi un numero intero con una frazione Step 6
    2. Dividi ogni forma intera per il denominatore della frazione. Il denominatore di una frazione indica in quante parti è divisa una forma intera. Dividi ogni forma intera nelle sue parti come indicato dalla frazione.
  • Ad esempio, se dividi per 34{displaystyle {frac {3}{4}}}{frac{3}{4}}, quindi il 4 al denominatore indica che devi dividere il tutto in quattro parti uguali.
    • Immagine titolata Dividi un numero intero con una frazione Step 7
    3. Ombreggia i gruppi che rappresentano la frazione. Poiché dividi il numero intero per la frazione, vedi quanti gruppi della frazione ci sono nel numero intero. Quindi prima indichi i gruppi. Può essere utile dare a ciascun gruppo un colore diverso, poiché alcuni gruppi hanno parti in due forme intere diverse. Lascia in bianco i pezzi rimanenti.
  • Ad esempio: immagina la parte 5 34{displaystyle {frac {3}{4}}}{frac{3}{4}}, poi colori tre quarti in un colore diverso per ogni gruppo. Nota che molti gruppi conterranno due quarti in un intero e un quarto in un altro intero.
    • Immagine titolata Dividi un numero intero con una frazione Step 8
    4. Conta il numero di interi gruppi. Questo ti darà il numero intero della tua risposta.
  • Ad esempio, avevi sei gruppi di 34{displaystyle {frac {3}{4}}}{frac{3}{4}} devi fare i cinque cerchi.
    • Immagine titolata Dividi un numero intero con una frazione Step 9
    5. Interpreta i pezzi rimanenti. Confronta il numero di pezzi che ti rimangono con un intero gruppo. La frazione di un gruppo che hai lasciato indica la frazione della tua risposta. Fai attenzione a non confrontare il numero di pezzi che hai con il numero di pezzi che hai con una forma intera perché questo ti darà la frazione sbagliata.
  • Ad esempio: dopo aver diviso le cinque forme in gruppi di 34{displaystyle {frac {3}{4}}}{frac{3}{4}}, hai due quarti, o 24{displaystyle {frac {2}{4}}}{displaystyle {frac {2}{4}}} di. Poiché un intero gruppo è composto da tre pezzi e tu hai due pezzi, la tua frazione lo è 23{displaystyle {frac {2}{3}}}{frac{2}{3}}.
    • Immagine titolata Dividi un numero intero con una frazione Step 10
    6. Scrivi la risposta. Combina i gruppi del numero intero con i gruppi della frazione per trovare il quoziente della tua somma di divisione originale.
  • Ad esempio: 5÷34=623{displaystyle 5div {frac {3}{4}}=6{frac {2}{3}}}{displaystyle 5div {frac {3}{4}}=6{frac {2}{3}}}.

    • Metodo 3 di 3: Esempi di problemi con soluzioni

    Immagine titolata Dividi un numero intero con una frazione Step 11
    1. Risolvere: Quanto spesso 12{displaystyle {frac {1}{2}}}{frac{1}{2}} in 8{ displaystyle 8}{ displaystyle 8}?
    • Perché il compito chiede di quanti gruppi 12{displaystyle {frac {1}{2}}}{frac{1}{2}} andando in 8 è una somma di divisione.
    • Fai una frazione di 8 trasformandola in un numeratore con denominatore 1: 8=81{displaystyle 8={frac {8}{1}}}{displaystyle 8={frac {8}{1}}}.
    • Trova il reciproco della frazione invertendo numeratore e denominatore: 12{displaystyle {frac {1}{2}}}{frac{1}{2}} diventa 21{displaystyle {frac {2}{1}}}{displaystyle {frac {2}{1}}}.
    • Moltiplica le due frazioni insieme: 81×21=161{displaystyle {frac {8}{1}}times {frac {2}{1}}={frac {16}{1}}}{displaystyle {frac {8}{1}}times {frac {2}{1}}={frac {16}{1}}}.
    • Semplificare, se necessario: 161=16{displaystyle {frac {16}{1}}=16}{displaystyle {frac {16}{1}}=16}.
    Immagine titolata Dividi un numero intero con una frazione Step 12
    2. Risolvere:16÷58{displaystyle 16div {frac {5}{8}}}{displaystyle 16div {frac {5}{8}}}.
  • Fai una frazione di 16 trasformandola in un numeratore con denominatore 1: 16=161{displaystyle 16={frac {16}{1}}}{displaystyle 16={frac {16}{1}}}.
  • Trova il reciproco della frazione invertendo numeratore e denominatore: 58{displaystyle {frac {5}{8}}}{displaystyle {frac {5}{8}}} diventa 85{displaystyle {frac {8}{5}}}{displaystyle {frac {8}{5}}}.
  • Moltiplica le due frazioni insieme: 161×85=1285{displaystyle {frac {16}{1}}times {frac {8}{5}}={frac {128}{5}}}{displaystyle {frac {16}{1}}times {frac {8}{5}}={frac {128}{5}}}.
  • Semplificare, se necessario: 1285=2535{displaystyle {frac {128}{5}}=25{frac {3}{5}}}{displaystyle {frac {128}{5}}=25{frac {3}{5}}}.
    • Immagine titolata Dividi un numero intero con una frazione Step 13
    3. Risolvi il seguente problema disegnando un diagramma. Rufus ha nove lattine di fagioli. Lei mangia tutti i giorni 23{displaystyle {frac {2}{3}}}{frac{2}{3}} una lattina. Per quanti giorni ha le lattine?
  • Disegna nove cerchi per rappresentare le nove lattine.
  • Perché lei 23{displaystyle {frac {2}{3}}}{frac{2}{3}} mangiare alla volta, dividere ogni cerchio in terzi.
  • Colora i gruppi di 23{displaystyle {frac {2}{3}}}{frac{2}{3}}.
  • Conta il numero di gruppi completi. Questo dovrebbe essere 13.
  • Interpreta i pezzi rimanenti. È rimasto un pezzo, e questo è 13{displaystyle {frac {1}{3}}}{frac{1}{3}}. Perché un intero gruppo 23{displaystyle {frac {2}{3}}}{frac{2}{3}} è che ti è rimasto mezzo gruppo. Quindi la frazione lo è 12{displaystyle {frac {1}{2}}}{frac{1}{2}}.
  • Combina il numero di gruppi di numeri interi e frazioni per trovare la risposta finale: 9÷23=1312{displaystyle 9div {frac {2}{3}}=13{frac {1}{2}}}{displaystyle 9div {frac {2}{3}}=13{frac {1}{2}}}.

    • It.FaqCartx.info / Educazione e comunicazione
    Condividi sui social network:
    Nuovo
    Superare la crisi delle vacanze
    Superare la crisi delle vacanze
    Sbarazzati del forte mal di schiena
    Sbarazzati del forte mal di schiena
    Diventare un regista
    Diventare un regista
    Cambiare la forma di una frase in inglese da attiva a passiva
    Cambiare la forma di una frase in inglese da attiva a passiva
    Ottenere il cut hm in pokémon rosso fuoco e verde foglia
    Ottenere il cut hm in pokémon rosso fuoco e verde foglia
    Sblocca qualcuno su facebook
    Sblocca qualcuno su facebook