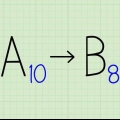Converti un Decimale Ripetuto in una Frazione: 9 Passaggi (con Immagini)

Contenuto

Passi
- Parte 1 di 2: Conversione di semplici decimali ripetuti
- Parte 2 di 2: Conversione di numeri con decimali ripetuti e non ripetuti

Un decimale ripetuto, chiamato anche decimale ripetuto, è un numero decimale contenente una cifra o un gruppo di cifre che si ripete indefinitamente a intervalli regolari. La ripetizione dei decimali può essere difficile con cui lavorare, ma possono anche essere convertiti in una frazione. A volte i decimali ripetuti sono indicati da una riga sopra le cifre ripetute. Il numero 3.7777 con 7 come cifra ripetuta, ad esempio, può anche essere scritto come 3.7. Per convertire un numero come questo in una frazione, scrivilo come un`equazione, moltiplica e sottrai per rimuovere il decimale ripetuto e risolvi l`equazione.

Passi

Parte 1 di 2: Conversione di semplici decimali ripetuti

Immagine titolata Converti decimali ripetuti in frazioni Step 1

1. Trova il decimale ripetuto. Ad esempio: il numero 0,4444 ha un decimale ripetuto 4. È un decimale ripetuto standard, nel senso che non c`è una parte non ripetuta nel numero decimale. Conta quante cifre decimali ripetute (ripetute) ci sono nel modello.

Quando la tua equazione è scritta, moltiplicala per 10^y`, per cuiy è uguale al numero di cifre ripetute nel pattern.
Nell`esempio di 0,4444, c`è una cifra che si ripete, quindi moltiplichi l`equazione per 10^1.
Per un decimale ripetuto di 0,4545, ci sono due numeri che si ripetono e quindi moltiplichi la tua equazione per 10^2.
Per tre numeri ripetuti, moltiplica per 10^3, ecc.

Immagine titolata Converti decimali ripetuti in frazioni Step 2

2. Riscrivi il decimale come equazione. Scrivilo in modo che x sia uguale al numero originale.In questo caso, l`equazione è x = 0.4444. Poiché c`è solo una cifra nel decimale ripetuto, moltiplica l`equazione per 10^1 (che equivale a 10).

Nell`esempio: dove x = 0,4444, poi 10x = 4,4444.

Nell`esempio x = 0,4545 ci sono due numeri ripetuti, quindi moltiplichi entrambi i membri dell`equazione per 10^2 (che equivale a 100), ottenendo 100x = 45.4545 prende.

Immagine titolata Converti decimali ripetuti in frazioni Step 3

3. Rimuovere il decimale ripetuto. Lo fai sottraendo x da 10x. Ricorda che quello che fai da un lato dell`equazione, devi farlo dall`altro lato, quindi:

10x – 1x = 4,4444 – 0,4444

Sulla sinistra hai 10x - 1x = 9x. Sul lato destro hai 4,4444 – 0,4444 = 4

Pertanto: 9x = 4

Immagine titolata Converti decimali ripetuti in frazioni Step 4

4. Risolvi per x. Una volta che sai a cosa è uguale 9x, puoi determinare a cosa è uguale x dividendo entrambi i membri dell`equazione per 9:

Sul lato sinistro dell`equazione hai 9x ÷ 9 = x. Sul lato destro dell`equazione hai 4/9

È per questo x = 4/9, e può essere il decimale ripetuto 0,4444 essere scritto come frazione 4/9.

Immagine titolata Converti decimali ripetuti in frazioni Step 5

5. Riduci la frazione. Converti la frazione nella sua forma più semplice (se presente) dividendo sia il numeratore che il denominatore per il massimo fattore comune.

Nell`esempio di 4/9 questa è la forma più semplice.

Parte 2 di 2: Conversione di numeri con decimali ripetuti e non ripetuti

Immagine titolata Converti decimali ripetuti in frazioni Step 6

1. Determina i numeri ripetuti. Non è raro che un numero abbia cifre non ripetute prima del decimale ripetuto, ma possono comunque essere convertite in frazioni.

Prendi ad esempio il numero 6.215151. Qui è 6.2 non ripetitivi e i numeri ripetitivi lo sono 15.
Nota di nuovo quante cifre ripetute ci sono nello schema, perché moltiplichi per 10^y in base a quel numero.
In questo esempio, ci sono due numeri ripetuti, quindi moltiplica l`equazione per 10^2.

Immagine titolata Converti decimali ripetuti in frazioni Step 7

2. Scrivi il problema come un`equazione e sottrai i decimali ripetuti. Di nuovo, se x = 6,215151, poi 100x = 621.5151. Per rimuovere i decimali ripetuti, sottrarre da entrambi i lati dell`equazione:

100x – x (= 99x) = 621.5151 – 6.215151 (= 615,3)

Quindi, 99x = 615,3

Immagine titolata Converti decimali ripetuti in frazioni Step 8

3. Risolvi per x. Poiché 99x = 615,3, dividi entrambi i membri dell`equazione per 99. Questo ti dà x = 615,3/99.

Immagine titolata Converti decimali ripetuti in frazioni Step 9

4. Rimuovere il decimale nel contatore. Fallo moltiplicando numeratore e denominatore per 10^z`, per cuiz è uguale al numero di decimali che devi spostare per eliminare il decimale. In 615.3 devi spostare il decimale di una posizione, il che significa che moltiplichi numeratore e denominatore per 10^1:

615,3×10 / 99 x 10 = 6153/990

Semplifica la frazione dividendo numeratore e denominatore per il massimo comune fattore (in questo caso 3) e ottieni x = 2.051 / 330