Esso binario (base 2) sistema numerico ha due possibili valori, solitamente rappresentati come 0 o 1, per ogni posizione in un numero. La differenza con il decimale (base 10) sistema numerico è che ci sono dieci valori possibili (0,1,2,3,4,5,6,7,8 o 9) per ogni posizione.
Per evitare confusione quando si utilizzano sistemi numerici diversi, la base di un numero può essere indicata aggiungendo un pedice dopo il numero.Ad esempio, il numero binario 10011100 può essere scritto in base 2 scrivendolo come 100111002.Il numero decimale 156 può essere scritto come 15610 o per intero come "centocinquantasei, base 10".
Poiché il sistema binario è il linguaggio macchina dei computer, i programmatori seri devono comprendere appieno come convertire i numeri binari in numeri decimali.La conversione nella direzione inversa, da decimale a binario, è spesso più difficile da imparare prima.
Nota: si tratta SOLO di calcoli e non di traduzioni ASCII.
Passi
Metodo 1 di 2: Metodo del sistema di posizionamento
1. In questo esempio useremo il numero binario 100110112 convertire in decimale. Elenca le potenze di due da destra a sinistra. Inizia con 2, questo ha il valore "1".Moltiplica gli esponenti per 1 per ogni potenza.Interrompi quando il numero di elementi nell`elenco è uguale al numero di cifre nel numero binario. Il numero nell`esempio, 10011011, ha 8 cifre, quindi l`elenco sarà simile a questo: 128, 64, 32, 16, 8, 4, 2, 1
2. Scrivi il numero binario sotto l`elenco.
3. Collega i numeri binari con potenze di due. Disegna linee che collegano ogni cifra binaria alla corrispondente seconda potenza sopra di essa.Inizia dalla prima cifra binaria, da destra, e continua fino ad aver collegato tutte le cifre binarie e le potenze.
4. Scorri tutte le cifre del numero binario. Se il numero è un 1, scrivi la seconda potenza corrispondente sotto la riga, direttamente sotto il numero.Se il numero è uno 0, scrivi uno 0 sotto la riga.
5. Somma i numeri sotto la linea. La somma dovrebbe essere 155. Questo è l`equivalente decimale del numero binario 10011011.Oppure, scritto con la base in pedice:
6. Se ripeti spesso questo metodo scoprirai di ricordare meglio i poteri di due, quindi puoi saltare il passaggio 1.
Metodo 2 di 2: Metodo del raddoppio
1. Questo metodo non utilizza poteri. Pertanto, è più adatto se vuoi convertire numeri più grandi a memoria, poiché devi solo ricordare il totale parziale.
2. Inizia con la cifra all`estrema sinistra del numero binario specificato. Per ogni numero successivo da sinistra a destra, raddoppia il totale precedente e aggiungilo al numero corrente. Ad esempio, per inserire il numero 10110012 per convertire in decimale, procediamo come segue:
3. 1011001 → 0 * 2 + 1 = 1
4. 1011001 → 1 * 2 + 0 = 2
5. 1011001 → 2 * 2 + 1 = 5
6. 1011001 → 5 * 2 + 1 = 11
7. 1011001 → 11 * 2 + 0 = 22
8. 1011001 → 22 * 2 + 0 = 44
9. 1011001 → 44 * 2 + 1 = 8910
10. Come il metodo del sistema di posizione, questo metodo può essere modificato per convertire da qualsiasi sistema numerico in un numero decimale.Il raddoppio è usato qui perché la base è due. Se il numero dato ha una base diversa, usa quella invece di 2. Ad esempio, se il numero ha una base di 37, scambia *2 con *37. Il risultato sarà sempre un numero decimale (base 10). :)
Consigli
- Allenati molto. Prova i numeri binari 110100012, 110012, e 111100012.I loro equivalenti decimali sono 20910, 2510, e 24110.
- Anche la calcolatrice fornita con Microsoft Windows può eseguire questa conversione per te, ma se sei un programmatore, è meglio che tu abbia una buona comprensione di come funziona questa conversione. Le opzioni di questo calcolatore possono essere trovate attraverso il "Visualizzazione" menu e poi "Scientifico" (o "programmatore"). Con Linux puoi usare calcolatore.
Avvertenze
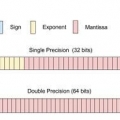
- Questo può essere usato per non firmato binario (solo numeri positivi), ma non per segno, virgola mobile o virgola fissa.
Articoli sull'argomento "Conversione di un numero binario in un numero decimale"