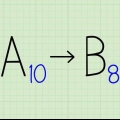Converti un Numero Decimale in Formato Binario ieee 754: 11 Passaggi (con Immagini)

A differenza degli esseri umani, i computer non utilizzano il sistema dei numeri decimali. Usano un sistema numerico binario o binario con due possibili cifre, 0 e 1. Quindi i numeri sono scritti in modo molto diverso in IEEE 754 (uno standard IEEE per rappresentare numeri binari con una virgola mobile) rispetto al tradizionale sistema decimale a cui siamo abituati. In questo articolo imparerai come scrivere un numero con precisione singola o doppia secondo IEEE 754. Per questo metodo, devi sapere come convertire i numeri in forma binaria. Se non sai come farlo, puoi impararlo attraverso l`articolo Converti Binario in Decimale studiare.

Passi

1. Scegli precisione singola o doppia. Quando si scrive un numero con precisione singola o doppia, i passaggi per una conversione riuscita saranno gli stessi per entrambi. L`unico cambiamento si verifica quando si converte l`esponente e la mantissa.

Per prima cosa dobbiamo capire cosa significa precisione singola. Nella vista a virgola mobile, qualsiasi numero (0 o 1) è considerato un `bit`. Pertanto, una singola precisione ha un totale di 32 bit divisi in tre diversi soggetti. Questi soggetti sono costituiti da un segno (1 bit), un esponente (8 bit) e una mantissa o frazione (23 bit).
La doppia precisione, d`altra parte, ha la stessa configurazione e le stesse tre parti della precisione singola: l`unica differenza è che sarà un numero più grande e più accurato. In questo caso il segno sarà 1 bit, l`esponente 11 bit e la mantissa 52 bit.
In questo esempio convertiremo il numero 85.125 in precisione singola secondo IEEE 754.

2. Separa il numero prima e dopo la virgola. Prendi il numero che vuoi convertire e scomponi il numero in modo da rimanere con un numero intero e un numero decimale. In questo esempio assumiamo il numero 85.125. Puoi separarlo nell`intero 85 e nel decimale 0,125.

3. Converti il numero intero in un numero binario. Questo sarà l`85 di 85.125, che diventerà 1010101 quando convertito in binario.

4. Converti la parte decimale in un numero binario. Questo è quindi 0,125 di 85,125, che diventa 0,001 in notazione binaria.

5. Combina le due parti del numero convertito in numeri binari. Il numero 85 è binario, ad esempio 1010101 e la parte decimale 0,125 è binaria 0,001. Se li combini con un punto decimale, ottieni 1010101.001 come risposta finale.

6. Converti il numero binario in notazione binaria scientifica. Puoi convertire il numero in notazione binaria scientifica spostando il punto decimale a sinistra finché non si trova a destra del primo bit. Questi numeri sono normalizzati, il che significa che il bit iniziale sarà sempre 1. Per quanto riguarda l`esponente, il numero di volte in cui si sposta il decimale è l`esponente nella notazione binaria scientifica.

Ricordiamo che spostando il decimale a sinistra si ottiene un esponente positivo, mentre spostando il decimale a destra si ottiene un esponente negativo.

Nel nostro esempio, devi spostare il decimale sei volte per portarlo a destra del primo bit. La notazione risultante diventa quindi

01, 010101001 * 2 6

${displaystyle 01.010101001*2^{6}}$ . Questo numero verrà utilizzato nei passaggi seguenti.

7. Determina il segno del numero e visualizzalo in notazione binaria. Ora determinerai se il numero originale è positivo o negativo. Se il numero è positivo, scrivi quel bit come 0 e se è negativo, come 1. Poiché il numero originale è 85,125 positivo, scrivi quel bit come 0. Questo è ora il primo bit del totale di 32 bit nella rappresentazione di precisione singola secondo IEEE 754.

8. Determina l`esponente in base alla precisione. C`è una distorsione fissa sia per la precisione singola che doppia. La distorsione del singolo esponente di precisione è 127, il che significa che dobbiamo aggiungere l`esponente binario trovato in precedenza. Quindi l`esponente che utilizzerai lo è 127+6 = 133.

La doppia precisione, come suggerisce il nome, è più accurata e può contenere numeri più grandi. Pertanto, il bias dell`esponente 1023. Qui si applicano gli stessi passaggi utilizzati per la precisione singola, quindi l`esponente che puoi utilizzare per determinare la doppia precisione è 1029.

9. Converti l`esponente in binario. Dopo aver determinato l`esponente finale, devi convertirlo in binario in modo che possa essere utilizzato nella conversione IEEE 754. Nell`esempio puoi convertire il 133 che hai trovato nell`ultimo passaggio in 10000101.

10. Determina la mantissa. L`aspetto mantissa, o la terza parte della conversione IEEE 754, è il resto del numero dopo il decimale della notazione binaria scientifica. Basta omettere l`1 davanti e copiare la parte decimale del numero moltiplicato per due. Nessuna conversione binaria richiesta! Nell`esempio, la mantissa diventa 010101001 di

01, 010101001 * 2 6

${displaystyle 01.010101001*2^{6}}$ .

11. Infine, combina tre parti in un numero.

Infine, combini tutto ciò che abbiamo calcolato finora nella tua conversione. Il numero inizierà prima con uno 0 o 1 che hai determinato nel passaggio 7 in base al segno. Nell`esempio inizi con uno 0.

Quindi hai l`esponente che hai determinato nel passaggio 9. Nell`esempio, l`esponente è 10000101.

Poi arriva la mantissa, la terza e ultima parte della conversione. L`hai derivato in precedenza quando hai preso la parte decimale della conversione binaria. Nell`esempio, la mantissa è 010101001.

Infine, combini questi numeri tra loro. L`ordine è segno-esponente-mantissa. Dopo aver collegato questi tre numeri binari, riempi il resto della mantissa con zeri.

Ad esempio, se 85.125 viene convertito nel formato binario IEEE 754, la soluzione è 0 10000101 010101001000000000000000.