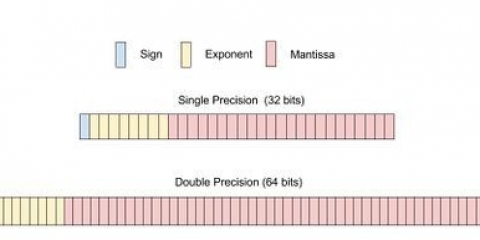
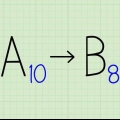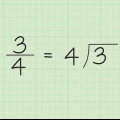Converti Binario in Decimale

Contenuto

Passi
Consigli

Il sistema numerico decimale ha dieci possibili valori (0,1,2,3,4,5,6,7,8 o 9) per ogni valore di posizione. Ciò contrasta con il sistema numerico binario che ha solo due valori possibili, spesso rappresentati da 0 o 1, per ogni valore di posizione. Per evitare confusione quando si utilizzano questi diversi sistemi numerici, la base di ogni singolo numero viene spesso indicata scrivendola in pedice. Ad esempio, il numero decimale 156 potrebbe essere indicato come 156₁₀ ed è letto come "centocinquantasei, base dieci". Il numero binario 10011100 può essere indicato come "base due" scrivendolo come 10011100₂. Poiché il sistema binario è il linguaggio interno dei computer elettronici, i programmatori seri dovrebbero sapere come convertire i decimali in binari e viceversa. Ecco come farlo.

Passi

Metodo 1 di 3: scelta di un metodo di conversione

Breve divisione per due con resto (facile per i principianti).
Confronto con potenze decrescenti di due e sottrazione.

Metodo 2 di 3: Metodo uno: dividere per due con resto

Questo metodo è molto più facile da capire se visualizzato su carta. Presuppone solo la divisione per due.

Immagine titolata Converti da decimale a binario Step 1

1. Stesura del problema. In questo esempio, prendiamo il numero decimale 156₁₀ converti in binario.

Scrivi il numero decimale come dividendo sottosopra "lunga divisione" simbolo.
Scrivi la base del rispettivo sistema (nel nostro caso "2" per binario) se il divisore è al di fuori della curva del simbolo di divisione.

Immagine titolata Converti da decimale a binario Step 2

2. Scrivi la risposta intera (quoziente) sotto il simbolo della divisione lunga e scrivi il resto (0 o 1) a destra del dividendo.

Fondamentalmente, se il dividendo è un numero pari, il resto binario sarà 0; se il dividendo è dispari il resto binario sarà 1.

Immagine titolata Converti da decimale a binario Step 3

3. Proseguendo verso il basso, dividi ogni nuovo quoziente per due e scrivi i resti a destra di ogni dividendo. Interrompi quando il quoziente è 0.

Immagine titolata Converti da decimale a binario Step 4

4. Iniziando dal resto inferiore, leggi la sequenza dei resti verso l`alto. Per questo esempio dovresti ora avere 10011100. Questo è l`equivalente binario del numero decimale 156. Oppure, scritto con pedice: 156₁₀ = 10011100₂

Questo metodo può essere adattato a decimali fino a ogni notazione da convertire. Il divisore è 2 perché il formato desiderato è. Se il risultato desiderato è un formato diverso, sostituire il 2 nel metodo con il formato desiderato. Ad esempio, se il risultato desiderato è la notazione 9, sostituire 2 con 9. Il risultato desiderato sarà quindi nel formato corretto.

Metodo 3 di 3: Metodo Due: Confronto con potenze decrescenti di due e sottrazione.

Immagine titolata Converti da decimale a binario Step 5

1. Scrivi i poteri di due in uno "sistema di numeri binari" da destra a sinistra. Inizia da 2, valuta come "1". Moltiplica l`esponente per 1 per ogni potenza. L`elenco, fino a dieci elementi, dovrebbe essere simile a questo. 512, 256, 128, 64, 32, 16, 8, 4, 2, 1

Immagine titolata Converti da decimale a binario Step 6

2. Trova la massima potenza che si adatta al numero che vuoi convertire in binario. In questo esempio convertiamo il numero decimale 156₁₀ a binario. Qual è il potere più grande che si inserisce in 156? Poiché 128 fit scriviamo un 1 come cifra binaria più a sinistra e sottraiamo 128 dal numero decimale, 156. Adesso ne hai 128.

Immagine titolata Converti da decimale a binario Step 7

3. Continua alla potenza inferiore successiva di due. Si adatta da 64 a 28? No, quindi scrivi uno 0 prima della cifra binaria successiva a destra.

Immagine titolata Converti da decimale a binario Step 8

4. Si adatta da 32 a 28?No, quindi scrivi uno 0.

Immagine titolata Converti da decimale a binario Step 9

5. Si adatta da 16 a 28?Sì, quindi scrivi un 1 e sottrai 16 da 28. Ora ne restano 12.

Immagine titolata Converti da decimale a binario Step 10

6. Può contenere 8 su 12?Sì, quindi scrivi un 1 e sottrai 8 da 12. Ora ne rimangono 4.

Immagine titolata Converti da decimale a binario Step 11

7. Adatta 4 (potenza di due) in 4 (decimale)?Sì, quindi scrivi un 1 e sottrai 4 da 4.Ora ne rimane 0.

Immagine titolata Converti da decimale a binario Step 12

8. Si adatta a 2 su 0?No, quindi scrivi uno 0.

Immagine titolata Converti da decimale a binario Step 13

9. Adatta 1 a 0?No, quindi scrivi uno 0.

Immagine titolata Converti da decimale a binario Step 14

10. Componi la risposta binaria. Dal momento che non ci sono più potenze di due nell`elenco, hai finito. Ora dovresti avere 10011100. Questo è l`equivalente binario del numero decimale 156. Oppure, scritto con pedice: 156₁₀ = 10011100₂

La ripetizione di questo metodo comporterà la memorizzazione dei poteri di due, consentendoti di saltare il passaggio 1.

Consigli

La conversione nell`altra direzione, da binario a decimale, è spesso più facile da imparare prima
la pratica. Prova il numero decimale 178₁₀, 63₁₀ e 8₁₀ convertire. Gli equivalenti binari sono 10110010₂, 00111111₂ e 00001000₂.Prova 209₁₀, 25₁₀ e 241₁₀ da convertire rispettivamente in 11010001₂, 00011001₂, 11110001₂ ottenere.
La calcolatrice presente nel tuo sistema operativo può eseguire questa conversione per te. Ma come programmatore stai meglio con una buona comprensione di come funziona questa conversione. Le opzioni di conversione della calcolatrice possono essere rese visibili nel menu "Statua" > "Programmatore".