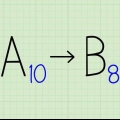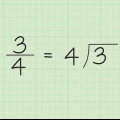16 = 1.048.576 16 = 65.536 16 = 4.096 16 = 256 16 = 16 Se il numero decimale che stai convertendo è maggiore di 1.048.576, quindi calcola le potenze superiori di 16 e aggiungilo all`elenco. 
Ad esempio, se tu 495 converti in esadecimale, quindi scegli 256 dall`elenco sopra. 
Nel nostro esempio, 495 ÷ 256 = 1.93... , ma a noi interessa solo il numero intero 1. La tua risposta è la prima cifra del numero esadecimale. In questo caso, poiché abbiamo diviso per 256, 1 è il numero al posto di "256-it." 
Moltiplica la tua ultima risposta per il divisore. Nel nostro esempio, 1 x 256 = 256. (In altre parole, l`1 del nostro numero esadecimale rappresenta il 256 con la base 10). Sottrai la tua risposta dal dividendo. 495 - 256 = 239. 
239 ÷ 16 = 14. Ancora una volta, ignoriamo tutte le cifre decimali. Questa è la seconda cifra del nostro numero esadecimale, il "16-e." Qualsiasi numero da 0 a 15 può essere rappresentato come una singola cifra esadecimale. Convertiamo alla notazione corretta alla fine di questo metodo. 
14 x 16 = 224. 239 - 224 = 15, quindi il resto è 15. 
L`ultimo "figura" del nostro numero esadecimale è 15, al posto del "unità." 
I numeri da 0 a 9 rimangono gli stessi. 10 = A; 11 = B; 12 = C; 13 = D; 14 = E; 15 = F Nel nostro esempio finiamo con i numeri (1)(14)(15). Nella corretta notazione, questo diventa il numero esadecimale 1EF. 
1EF → (1)(14)(15) Da destra a sinistra, 15 è in 16 = 1a posizione. 15 x 1 = 15. La cifra successiva da sinistra è nella posizione 16 = 16. 14 x 16 = 224. La cifra successiva è nella posizione 16 = 256. 1 x 256 = 256. Li sommiamo tutti insieme, 256 + 224 + 15 = 495, il nostro numero originale. 

Per trovare il resto, moltiplica la risposta per il divisore, quindi sottrai il risultato dal dividendo. Nel nostro esempio, 317.547 - (19.846 x 16) = 11. Converti la cifra in formato esadecimale utilizzando la tabella di conversione dei numeri piccoli nella parte superiore di questa pagina dell`articolo. 11 giri B nel nostro esempio. 
Nel nostro esempio, 19.846 / 16 = 1.240. resto = 19.846 - (1.240 x 16) = 6. Questa è la penultima cifra del nostro numero esadecimale. 
Prendi l`ultimo quoziente e dividilo ancora per 16. 1.240 / 16 = 77 resto 8. 77 / 16 = 4 resto 13 = D. 4 < 16, quindi 4 è la prima cifra. 
La nostra ultima risposta è 4D86B. Per controllare il tuo lavoro, riconvertisci ogni cifra nel numero decimale, moltiplicato per potenze di 16, e somma i risultati. (4 x 16) + (13 x 16) + (8 x 16) + (6 x 16) + (11 x 1) = 317.547, il nostro numero decimale originale.
Converti da decimale a esadecimale
Contenuto
L`esadecimale è un sistema numerico in base sedici. Ciò significa che ci sono 16 simboli per indicare un numero, con A, B, C, D, E e F aggiunti alle solite dieci cifre. La conversione da decimale a esadecimale è più difficile del contrario. Prenditi il tempo per imparare questo perché è più facile evitare errori una volta capito perché la conversione funziona.
Piccole conversioni di numeri
| Decimale | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Esadecimale | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | un | B | C | D | e | F |
Passi
Metodo 1 di 2: Metodo intuitivo

1. Usa questo metodo se non conosci i numeri esadecimali. Dei due approcci in questo articolo, questo è il più facile da seguire per la maggior parte delle persone. Se hai già familiarità con le diverse basi, prova quella più veloce metodo come indicato di seguito.
- Se non hai dimestichezza con i numeri esadecimali, impara prima i concetti di base.

2. Scrivi i poteri di 16. Ogni cifra all`interno del sistema esadecimale rappresenta una potenza diversa di 16, proprio come una cifra decimale è una potenza di 10. Questo elenco di poteri di 16 tornerà utile durante la conversione:

3. Trova la potenza massima di 16 che rientra nel numero decimale. Annota il numero decimale che vuoi convertire. Utilizzare l`elenco sopra come riferimento. Trova la potenza massima di 16 inferiore al numero decimale.

4. Dividi il numero decimale per questa potenza di 16. Fermati al numero intero e ignora ogni cifra dopo il punto decimale della risposta.

5. Trova il resto. Questo ti dice cosa resta del numero decimale da convertire. Ecco come puoi calcolarlo, proprio come con una lunga divisione:

6. Dividi il resto per la successiva potenza superiore di 16. Usa di nuovo la tua lista di poteri di 16 come riferimento. Continua in questo modo alla potenza minima di 16. Dividi il resto per quel valore per trovare la cifra successiva del tuo numero esadecimale. (Se il resto è inferiore a questo numero, la cifra successiva è 0.)

7. Determina di nuovo il resto. Come prima, moltiplica la risposta per il divisore e sottraila dal dividendo. Questo è il resto che deve ancora essere convertito.

8. Ripeti finché non hai un resto inferiore a 16. Una volta che il resto è compreso tra 0 e 15, può essere espresso con una singola cifra esadecimale. Scrivi questo come ultimo numero.

9. Scrivi la tua risposta nella notazione corretta. Ora sai quali sono tutte le cifre del tuo numero esadecimale. Ma finora li abbiamo scritti solo in base dieci. Per scrivere ogni cifra nella corretta notazione esadecimale, convertili usando questa guida:

10. Controlla il tuo lavoro. Controllare la tua risposta è facile quando capisci come funzionano i numeri esadecimali. Converti ogni cifra in forma decimale e moltiplicale per la sedicesima potenza per quella posizione di base. Ecco cosa dobbiamo fare per il nostro esempio:
Metodo 2 di 2: Metodo rapido (con riposo)

1. Dividi il numero decimale per 16. Tratta questa divisione come una divisione intera. In altre parole, ti fermi a una risposta con un numero intero, invece di calcolare i numeri decimali.
- Cerchiamo di essere un po` più ambiziosi riguardo a questo esempio e al numero decimale 317.547 convertire. Calcola 317.547 ÷ 16 = 19.846, e ignora i decimali.

2. Scrivi il resto in notazione esadecimale. Ora che hai diviso il numero per 16, il resto è la parte che non rientra più nella posizione dei 16 o superiore. Pertanto, il resto deve venire alla posizione delle unità, esso Ultimo cifra del numero esadecimale.

3. Ripeti questo processo con il quoziente. Hai convertito il resto in una cifra esadecimale. Ora per continuare a convertire il quoziente, dividilo di nuovo per 16. Il resto è la penultima cifra del numero esadecimale. Funziona con la stessa logica di cui sopra: il numero originale è ora diviso per (16 x 16 =) 256, quindi il resto è la parte del numero che si adatta alla posizione dei 256. Conosciamo già le unità, il resto deve essere al posto dei 16.

4. Ripeti fino ad ottenere un quoziente inferiore a 16. Non dimenticare di convertire un resto da 10 a 15 in formato esadecimale. Nota qualsiasi riposo lungo il percorso. L`ultimo quoziente (meno di 16) è la prima cifra del tuo numero. Continuiamo con l`esempio:

5. Finisci il numero. Come accennato in precedenza, determini ogni cifra del numero esadecimale da destra a sinistra. Controlla il tuo lavoro per assicurarti di averli scritti nell`ordine corretto.
Consigli
- Per evitare confusione quando si utilizzano i diversi sistemi numerici, è possibile scrivere la base come pedice. Ad esempio, 51210 è poi "512 con base 10," un numero decimale ordinario. 51216 si intende "512 con base 16," equivalente al numero decimale 1.29810.
Articoli sull'argomento "Converti da decimale a esadecimale"
Condividi sui social network:
Popolare