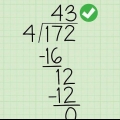
Nell`esempio vuoi determinare quante volte 6 va in 2. Poiché 6 è maggiore di 2, la risposta è 0. Se lo desideri, puoi posizionare uno 0 direttamente sopra il 2 come localizzatore e rimuoverlo in seguito. Puoi facoltativamente lasciare lo spazio aperto e passare al passaggio successivo. 
Se la risposta precedente era 0, come nell`esempio, espandere il numero di 1 cifra. In questo caso determinerai quante volte 6 va in 25. Se il divisore ha più di 2 cifre, potrebbe essere necessario utilizzare non 2 ma 3 cifre del dividendo per la prima divisione. Lavora con numeri interi. Se usi una calcolatrice, vedrai la divisione 25/6 = 4167. La divisione lunga arrotonda sempre per difetto al numero intero più vicino, quindi la risposta in questo caso è 4. 
È importante nella divisione lunga assicurarsi che i numeri siano allineati correttamente. Lavora con precisione, altrimenti commetterai errori. In questo esempio, stai mettendo 4 su 5, perché stiamo dividendo 25 per 6. 

Nell`esempio 6 * 4 = 24. Dopo aver incluso un 4 nel quoziente, scrivi il numero 24 sotto 25, ben allineato. 


Poiché il 6 nell`esempio non rientra in 1, dovrai aggiungere il numero successivo. In questo caso, prendi lo zero da 250 e lo metti accanto all`1, rendendolo uguale a 10, che starebbe 6. 
Nell`esempio si determina il numero di volte in cui 6 va in 10. Scrivi quel numero (1) nel quoziente, sopra il dividendo. Quindi moltiplica 6 per 1 e sottrai il risultato da 10. Se corretto, restituisce 4. Se il dividendo ha più di 3 cifre, continua a ripetere questa procedura finché non le hai avute tutte. Ad esempio, se avessimo iniziato con 2.506 grammi di funghi, avremmo preso il 6 in basso e lo avremmo posizionato accanto al 4. 

Nell`esempio, poiché 250 è un numero intero, ogni numero dopo la virgola è uguale a 0, che finisce per essere 250.000. 
Nell`esempio calcoli 40 diviso per 6. Aggiungi quel numero (6) al quoziente sopra il dividendo e dopo la virgola. Quindi moltiplica 6 per 6 e sottrai il risultato da 40. Ora dovresti tornare alle 4. 
Nell`esempio potresti andare avanti all`infinito e finire con 6 nella risposta più e più volte. Arrotonda questo valore per eccesso a 41,67, perché 6 è maggiore di 5 ed è quindi arrotondato per eccesso. In alternativa, puoi indicare un decimale ripetuto con una breve linea orizzontale attraverso il decimale ripetuto. Nell`esempio sembra 41.6, con un trattino attraverso il 6. 
Se ora hai notato un localizzatore, ora dovresti anche rimuoverlo. Nell`esempio in cui ti è stato chiesto il peso di 1 fungo in una scatola da 250 grammi, dovrai dare la risposta in grammi. Quindi, la risposta finale: 41,67 grammi.
Fai una lunga divisione
Contenuto
La divisione lunga è una parte normale della matematica e un metodo per risolvere una divisione e trovare il resto, solitamente utilizzato per i numeri più grandi. Imparare i passaggi di base della divisione lunga ti consente di dividere numeri di lunghezza arbitraria, sia interi che decimali. Questo è facile da imparare e questa abilità ti aiuterà a capire la matematica, qualcosa che ti aiuterà a scuola e per il resto della tua vita.
Passi
Parte 1 di 4: Condividi

1. Annota la somma. Scrivi il dividendo (il numero da dividere) a destra, sotto il simbolo di divisione, e il divisore (il numero da dividere) a sinistra, al di fuori del simbolo di divisione.
- Il quoziente (la risposta) è in definitiva in alto, direttamente sopra il dividendo.
- Lascia abbastanza spazio sotto il dividendo per le sottrazioni.
- Un esempio: hai 6 funghi in una scatola da 250 grammi, quanto pesa in media ogni fungo? Stiamo dividendo 250 per 6. Il 6 va all`esterno e il 250 all`interno.

2. Condividi il primo numero. A questo punto, lavorando da sinistra a destra, determini quante volte il divisore va nella prima cifra del dividendo.

3. Condividi i prossimi 2 numeri. Se il divisore è maggiore della prima cifra del dividendo, prova a utilizzare le prime 2 cifre del dividendo.

4. Annota la prima cifra del quoziente. Posiziona il numero di volte in cui il divisore entra nella prima cifra (o cifre) del dividendo sopra le cifre appropriate.
Parte 2 di 4: Moltiplicazione

1. Moltiplica il divisore. Moltiplica il divisore per il numero che hai appena scritto sopra il dividendo. Nell`esempio, questa è la prima cifra del quoziente.

2. Nota il prodotto. Metti il risultato della moltiplicazione del passaggio 1 sotto il dividendo.

3. Disegna una linea. Metti una linea sotto il prodotto della tua moltiplicazione (24) dall`esempio.
Parte 3 di 4: Sottrazione e diminuzione di un numero

1. Sottrarre il prodotto. Sottrarre il numero che hai scritto sotto il dividendo dalle cifre sopra di esso. Nota il risultato sotto la linea che hai appena disegnato.
- Nell`esempio, sottraiamo 24 da 25, che dà 1.
- Non sottrarre questo numero dall`intero dividendo, ma solo dal numero che hai utilizzato nel passaggio 1 e nel passaggio 2. Quindi sottrarre 24 non da 250, ma da 25.

2. Abbassa il numero successivo. Scrivi la cifra successiva del dividendo dopo il risultato della somma meno.

3. Ripetere l`intera procedura. Dividi il nuovo numero per il divisore e scrivi il risultato sopra il dividendo, come cifra successiva del tuo quoziente.
Parte 4 di 4: Trovare il resto o il decimale

1. Annota il resto della divisione. A seconda dello scopo della divisione, potresti cercare un numero intero più un resto.
- In questo esempio il resto è 4, perché 4 non è divisibile per 6 e non ci sono più cifre rimaste.
- Scrivi il resto del quoziente con a "R" prima di. Nell`esempio puoi già scrivere la risposta "41r4."
- Puoi fermarti ora se non è possibile esprimere la risposta in parti più piccole. Ad esempio, supponiamo di voler calcolare quante auto sono necessarie per trasportare un certo numero di persone. Non ha molto senso pensare in termini come mezza macchina o un quarto di macchina.
- Se prevedi di calcolare un decimale, puoi saltare questo passaggio.

2. Aggiungi un punto decimale ad esso. Se intendi dare la risposta in cifre dopo la virgola anziché il resto, metti una virgola dove altrimenti interromperesti il calcolo. Fallo sia per il dividendo che per il quoziente.

3. Continuare. Ora hai più numeri da spostare verso il basso (tutti zeri). Abbassa uno zero e continua come nel passaggio precedente, determinando quante volte il divisore si inserisce nel nuovo numero.

4. Fermati e finisci. In alcuni casi noterai che quando inizi a risolvere il decimale, numeri o gruppi di numeri continuano a ripetersi. Questo è un segno che puoi fermarti e finire la risposta.

5. Posizionare l`unità dopo la risposta (se presente). Se lavori con unità, come grammi, gradi o litri, puoi inserirle dopo la risposta dopo che tutti i calcoli sono stati completati.
Consigli
- Se hai abbastanza tempo, è una buona idea fare i tuoi calcoli prima su carta e poi con una calcolatrice o un computer. Ricorda che anche le macchine non danno sempre la risposta giusta, per vari motivi. Se si è verificato un errore, ricontrollare utilizzando i logaritmi. Fare le somme delle divisioni a mano piuttosto che con una macchina è meglio per le tue capacità e comprensione di matematica.
- Un modo per ricordare i passaggi della divisione lunga è: "De Vos Al Pane." D sta per divisione, V per moltiplicazione, A per sottrazione e B per riduzione.
- Trova esempi dalla pratica. Questo aiuta nell`apprendimento di questo metodo perché vedi come usarlo.
- Inizia con semplici calcoli. Questo ti dà la sicurezza e le competenze necessarie per essere in grado di svolgere compiti più difficili.
Articoli sull'argomento "Fai una lunga divisione"
Condividi sui social network:
Simile
Popolare