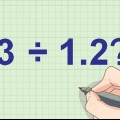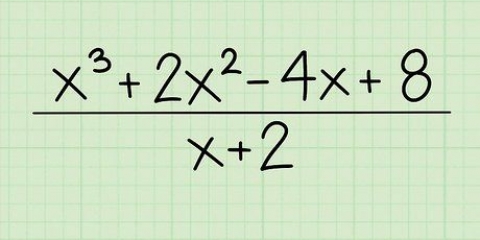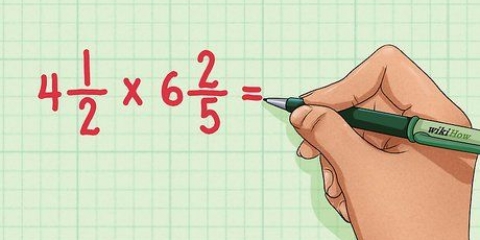Nell`esercizio n. 1 (5厂65), 5 è il denominatore e 6 è la prima cifra del numeratore (65). 5 va in 6 una volta, quindi metti un 1 sul segno di divisione, sopra il 6. Nell`esercizio n. 2 (3厂136), 3 (il divisore) non rientra completamente in 1 (la prima cifra del numeratore). In questo caso, scrivi uno 0 sopra il segno di divisione, sopra l`1. 
Nell`esercizio n. 1 (5厂65), moltiplica il numero sopra la barra (1) per il denominatore (5), ottenendo 1 x 5 = 5, e posiziona la risposta (5) appena sotto 6 di 65. Nell`esercizio n. 2 (`3厂136) c`è uno zero sopra il segno di divisione, quindi se lo moltiplichi per 3 (il denominatore), il risultato è zero. Scrivi uno zero su una nuova riga appena sotto 1 di 136. 
Nell`esercizio n. 1 (5厂65), sottrarre il 5 (il prodotto nella nuova riga) dal 6 sopra di esso (la prima cifra del numeratore): 6 - 5 = 1. Posiziona il risultato (1) in un`altra nuova riga direttamente sotto 5. Nell`esercizio n. 2 (3厂136) sottrai lo 0 (il prodotto nella nuova riga) dall`1 in alto a destra (la prima cifra del contatore). Posiziona il risultato (1) in un`altra nuova riga direttamente sotto lo 0. 
Nell`esercizio n. 1 (5厂65), abbassa il 5 di 65 in modo che sia prossimo all`1 ottenuto sottraendo 5 da 6. Ora ce ne sono 15 in questa riga. Nell`esercizio n. 2 (3厂136), abbassa il 3 di 136 e posizionalo accanto all`1, ottenendo 13. 
Per continuare 5厂65, dividi il nuovo numero (15) per 5 (il denominatore) e scrivi il risultato (3, perché 15 ÷ 5 = 3) a destra dell`1 sopra il segno di divisione. Quindi moltiplichi questo 3 sopra il segno di divisione per 5 (il denominatore) e scrivi il risultato (15, perché 3 x 5 = 15) under 15 sotto il segno di divisione. Infine, sottrai 15 da 15 e scrivi 0 in una nuova riga inferiore. Il problema di esempio n. 1 è ora completo, poiché non ci sono più numeri da ridurre al denominatore. La risposta (13) è sopra il segno di divisione. 
Per 3厂136: Determina quante volte 3 va completamente in 13 e scrivi la risposta (4) a destra dello 0 sopra il segno di divisione. Quindi moltiplica 4 per 3 e scrivi la risposta (12) sotto 13. Infine, sottrai 12 da 13 e scrivi la risposta (1) sotto 12. 
Per 3厂136: Continua il processo per il round successivo. Abbassa il 6 di 136, lasciando 16 nella riga inferiore. Dividi 16 per 3 e scrivi il risultato (5) sopra il segno di divisione. Moltiplica 5 per 3 e scrivi il risultato (15) in una nuova riga inferiore. Sottrarre 15 da 16 e scrivere il risultato (1) in una nuova riga inferiore. Poiché non ci sono più cifre da includere nel numeratore, hai finito con il problema e l`1 sulla riga inferiore è il resto (il numero che rimane). Scrivilo sopra il segno di divisione, possibilmente con una `r.`prima in modo che la tua risposta finale `45 r.1` diventa. 

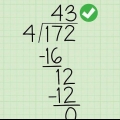
In questo problema, 4 (il denominatore) rientra in 5 (la prima cifra del numeratore) una volta, con resto di 1 (5 ÷ 4 = 1 r.1). Posiziona il quoziente, 1, sopra la linea di divisione lunga. Metti un piccolo apice 1 accanto al 5, per ricordare a te stesso che avevi un resto di 1. Il 518 sotto la linea di divisione dovrebbe ora apparire così: 518. 
Nel problema, il numero formato dal resto e dal secondo numero del numeratore è 11. il denominatore (4), va in 11 due volte, lasciando un resto di 3 (11 ÷ 4 = 2 r.3) rimane. Scrivi il 2 sopra la linea di divisione (dandoti 12) e il 3 come numero in apice accanto all`1 in 518. Il contatore originale, 518, ora dovrebbe apparire così: 518. 
Nel problema, 38 è il numero successivo (e ultimo) del numeratore -- il resto 3 del passaggio precedente e il numero 8 è l`ultimo termine del numeratore. Il denominatore (4) va in 38 nove volte con resto di 2 (38 ÷ 4 = 9 r.2), perché 4 x 9 = 36, che è due meno di 38. Scrivi quest`ultimo resto (2) sopra la linea di divisione per completare la tua risposta. Quindi la tua ultima risposta sopra il divisore è 129 r.2.. 

In questo problema di esempio, invertiremo 5/8 in modo che l`8 sia in alto e il 5 in basso. 
Ad esempio: 3/4 x 8/5. 
In questo caso, i numeratori sono 3 e 8, e 3 x 8 = 24. 
I denominatori sono 4 e 5 nel problema, e 4 x 5 = 20. 
Nell`incarico: 3/4 x 8/5 = 24/20. 
Nel caso di 24/20, 4 è il numero più grande che va alla pari sia in 24 che in 20. Puoi confermarlo scrivendo tutti i divisori di entrambi i numeri e scegliendo il numero più grande che sia un divisore di entrambi: 24: 1, 2, 3, 4, 6, 8, 12, 24 20: 1, 2, 4, 5, 10, 20 Poiché 4 è il massimo comune divisore di 24 e 20, dividi entrambi i numeri per 4 per semplificare la frazione. 24/4 = 6 20/4 = 5 24/20 = 6/5. Così: 3/4 5/8 = 6/5 
Nel problema, 5 va in 6 una volta con un resto di 1. Quindi il nuovo intero è 1, il nuovo numeratore è 1 e il denominatore rimane 5. Il risultato: 6/5 = 1 1/5. 

Nell`incarico: 8 - 5 = 3. 
Così: 3 3 = 3. 

Nel problema, tutto ciò che devi fare è spostare la virgola decimale di una posizione sia per il denominatore che per il numeratore. Quindi: 0,5 diventa 5 e 65,5 diventa 655. Tuttavia, se i numeri nel problema fossero 0,5 e 65,55, sposteresti la virgola decimale di due posizioni in 65,55, rendendolo 6555. Di conseguenza, dovresti anche spostare la virgola decimale di 0,5 di due posizioni. Per fare ciò, aggiungi uno zero alla fine e fallo 50. 
Nell`istruzione, il decimale viene in 655 dopo gli ultimi 5 (come 655.0). Quindi scrivi il punto decimale sopra la linea di divisione direttamente sopra il punto decimale in 655. 
Dividi il centesimo (6) per 5. Quindi ottieni 1, con il resto 1. Metti 1 al centesimo posto in cima alla linea di divisione lunga e sottrai 5 da 6 sotto il numero sei. Il resto, 1, rimane. Abbatti i primi cinque nel 655 e ottieni il numero 15. Dividi 15 per 5 e ottieni 3. Posiziona i tre sopra il carattere della divisione lunga, accanto all`1. Abbatti gli ultimi 5. Dividi 5 per 5 e ottieni 1: posiziona l`1 sopra il carattere di divisione lungo. Non c`è resto, poiché 5 va una volta su 5. La risposta è il numero sopra il segno di divisione lungo (131), quindi 655 5 = 131. Se estrai una calcolatrice, vedrai che questa è anche la risposta alla divisione originale: 65,5 0,5.
Fai le somme di divisione
Contenuto
La divisione è una delle quattro principali operazioni aritmetiche, insieme ad addizione, sottrazione e moltiplicazione. Oltre ai numeri interi, puoi anche dividere decimali, frazioni o esponenti. Puoi fare una divisione lunga o, se uno dei numeri è una singola cifra, una divisione breve. Inizia a padroneggiare la divisione lunga, però, perché questa è la chiave dell`intera operazione.
Passi
Metodo 1 di 5: Divisione lunga

1. Scrivi il problema usando asegno di divisione lunga. Il segno di divisione lunga( 厂 ) ha l`aspetto di una "parentesi finale" con un numero al di sotto. Metti il denominatore, il numero che stai dividendo, all`esterno del segno di divisione lungo, e il numeratore, il numero che stai dividendo, all`interno del segno di divisione lungo .
- Esempio di problema n. 1 (principiante): 65 5. Metti il 5 fuori dalla divisione e il 65 al suo interno. Dovrebbe sembrare 5厂65, ma con il 65 sotto la linea orizzontale.
- Esempio di esercizio n. 2 (avanzato): 136 3. Metti il 3 fuori dalla divisione e il 136 al suo interno. Dovrebbe sembrare 3厂136, ma con il 136 sotto la linea orizzontale.

2. Dividi la prima cifra del numeratore per il denominatore. In altre parole, scopri quante volte il denominatore (il numero al di fuori del segno di divisione) va nella prima cifra del numeratore. Posiziona il risultato intero sopra il segno di divisione, appena sopra la prima cifra del denominatore.

3. Moltiplica il numero sopra il segno di divisione per il denominatore. Prendi il numero che hai scritto appena sopra la divisione e moltiplicalo per il denominatore (il numero a sinistra della divisione). Scrivi il risultato in una nuova riga sotto il numeratore, allineata con la prima cifra del numeratore.

4. Sottrarre il prodotto (risultato della moltiplicazione) dalla prima cifra del numeratore. In altre parole, sottrai il numero che hai appena scritto nella nuova riga sotto il numeratore dal numero nel numeratore direttamente sopra di esso. Scrivi il risultato in una nuova riga, allineata sotto i numeri della sottrazione.

5. Abbassa la seconda cifra del contatore. Porta la seconda cifra del contatore in basso nella nuova riga in basso, appena a destra del risultato della sottrazione che hai appena ottenuto.

6. Ripeti la divisione lunga (attività n. 1). Questa volta usa il numeratore (il numero a sinistra del segno di divisione) e il nuovo numero nella riga in basso (il risultato del tuo primo giro di matematica e la cifra che hai portato giù). Come prima, dividi, moltiplica e sottrai i tuoi numeri per ottenere il risultato.

7. Ripeti la divisione lunga (attività n. 2). Come prima, inizia con la divisione, la moltiplicazione e poi la sottrazione.

8. Fai un altro giro di divisione lungo e ottieni il resto (attività n. 2). Quando hai finito con questo problema, nota che c`è un resto (cioè un numero rimasto alla fine del tuo calcolo). Metti questa pausa accanto alla tua intera risposta.
Metodo 2 di 5: Breve divisione

1. Usa un trattino per scrivere il problema. Metti il denominatore, il numero per cui stai dividendo, fuori (ea sinistra) della linea di divisione. Posiziona il numeratore, il numero che stai per dividere, all`interno (a destra e sotto) della linea di divisione.
- a veloce da condividere, può il denominatore essere costituito da una sola cifra.
- Incarico: 518 4. In questo caso, il 4 sarà fuori dalla linea di divisione e il 518 sarà all`interno di essa.

2. Dividi la prima cifra del numeratore per il denominatore. In altre parole, determina quante volte il numero al di fuori del divisore rientra nella prima cifra del numero all`interno del divisore. Scrivi l`intero del risultato sopra la barra di divisione e scrivi qualsiasi resto in apice accanto alla prima cifra del numeratore.

3. Dividi il resto e la seconda cifra del numeratore per il denominatore. Tratta il numero in apice che indica il resto come una cifra a tutti gli effetti e combinalo con la cifra del numeratore immediatamente a destra di esso. Determina quante volte il denominatore va completamente in questo nuovo numero a 2 cifre e scrivi il numero intero e qualsiasi resto come hai fatto prima.

4. Ripeti l`operazione finché non hai attraversato l`intero contatore. Continua a determinare quante volte il denominatore va nel numero formato dalla cifra successiva del numeratore e il resto in apice immediatamente a sinistra di esso. Una volta che hai esaminato tutte le cifre sul contatore, hai la tua risposta.
Metodo 3 di 5: Dividere le frazioni

1. Scrivi la somma della divisione in modo che le due frazioni siano una accanto all`altra. a dividere le frazioni, scrivi la prima frazione seguita dal simbolo di divisione (÷) e poi la seconda frazione.
- Ad esempio, la dichiarazione potrebbe essere qualcosa del tipo: 3/4 5/8. Per comodità, usa linee orizzontali anziché diagonali per separare il numeratore (numero in alto) e il denominatore (numero in basso) di qualsiasi frazione.

2. Invertire numeratore e denominatore della seconda frazione. La seconda frazione diventa il proprio inverso.

3. Cambia la barra di divisione in un segno di moltiplicazione. Per dividere le frazioni, moltiplica la prima frazione per il reciproco della seconda.

4. Moltiplica i numeratori delle frazioni. Segui la stessa procedura della moltiplicazione di due frazioni.

5. Moltiplica i denominatori delle frazioni allo stesso modo. Ancora una volta, questo è esattamente ciò che faresti per moltiplicare due frazioni.

6. Metti il prodotto dei numeratori sopra il prodotto dei denominatori. Ora che hai moltiplicato i numeratori e i denominatori di entrambe le frazioni, puoi formare il prodotto delle due frazioni.

7. Semplifica la frazione, se necessario. Per semplificare la frazione, determinare il massimo comun divisore, o il numero più grande che rientra in entrambi i numeri nella sua interezza, quindi dividi sia il numeratore che il denominatore per quel numero.

8. Riscrivi la frazione come un numero misto, se necessario. Per fare ciò, dividi il numeratore per il denominatore e scrivi la risposta come numero intero. Il resto (il numero che rimane) è il numeratore della nuova frazione. Il denominatore della frazione rimane lo stesso.
Metodo 4 di 5: Dividere gli esponenti

1. Assicurati che gli esponenti abbiano la stessa base. Puoi dividere gli esponenti se hanno la stessa base. Se non hanno la stessa base, dovrai manipolarli finché non lo faranno, se puoi.
- Se stai appena iniziando con questo, prima fai un problema in cui entrambi gli esponenti hanno già la stessa base. Ad esempio: 3 3.

2. Sottrarre gli esponenti l`uno dall`altro. Basta sottrarre il secondo esponente dal primo. Non preoccuparti per la base per ora.

3. Posiziona il nuovo esponente sopra la base originale. Basta scrivere il nuovo esponente sopra la base originale. È tutto!
Metodo 5 di 5: divisione dei numeri decimali

1. Scrivi il problema con un trattino. Posiziona il denominatore, il numero per cui stai dividendo, all`esterno (ea sinistra) della barra di divisione lunga, e il numeratore, il numero per cui stai dividendo, all`interno della barra di divisione lunga. a dividere i decimali, convertire prima i decimali in numeri interi.
- Nell`esempio 65,5 0,5 è posizionato 0,5 fuori dalla linea di divisione e 65,5 all`interno di essa.

2. Sposta i punti decimali allo stesso modo per creare due numeri interi. Basta far scorrere i punti decimali verso destra finché non si trovano alla fine di ogni numero. Assicurati di spostarli dello stesso numero di posizioni per ogni numero -- se devi spostare la virgola di due posizioni nel denominatore, fai lo stesso per il numeratore.

3. Posiziona il punto decimale direttamente sopra la linea di divisione. Metti un decimale sul segno di divisione lungo direttamente sopra il decimale nel numeratore.

4. Risolvi il problema eseguendo la divisione lunga. Per dividere 655 per 5, procedi come segue:
Articoli sull'argomento "Fai le somme di divisione"
Condividi sui social network:
Popolare