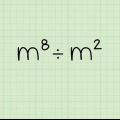Dividere Sinteticamente i Polinomi: 12 Passaggi (con Immagini)

Contenuto

Passi
Consigli

La divisione sintetica è un metodo abbreviato per dividere i polinomi in cui dividi i coefficienti dei polinomi per rimuovere variabili ed esponenti. Ciò consente di lavorare durante questo calcolo allo stesso modo della normale divisione lunga. Se vuoi sapere come dividere sinteticamente i polinomi, segui i passaggi seguenti.

Passi

Immagine titolata Divide Polynomials Using Synthetic Division Step 1

1. Scrivi il problema. Ad esempio, dividi x + 2x - 4x + 8 per x + 2. Scrivi la prima equazione quadratica, il dividendo, al numeratore e scrivi la seconda equazione, il divisore, al denominatore.

Immagine titolata Divide Polynomials Using Synthetic Division Step 2

2. Invertire il segno della costante nel divisore. La costante nel divisore, x + 2, è positiva, quindi l`inverso del segno della costante è -2.

Immagine titolata Divide Polynomials Using Synthetic Division Step 3

3. Posiziona questo numero fuori dalla parte al di fuori del segno di divisione. Il segno di divisione sembra un arretrato"l." Posiziona il termine -2 a sinistra di questo simbolo.

Immagine titolata Divide Polynomials Using Synthetic Division Step 4

4. Annota tutti i coefficienti del dividendo all`interno del segno di divisione. Scrivi i termini da sinistra a destra come appaiono. Questo è simile a questo: -2| 12-48.

Immagine titolata Divide Polynomials Using Synthetic Division Step 5

5. Abbassa il primo coefficiente. Posiziona il primo coefficiente, 1, sotto se stesso. Questo assomiglia a questo:

-2| 1 2 -4 8
↓
1

Immagine titolata Divide Polynomials Using Synthetic Division Step 6

6. Moltiplica il primo coefficiente per il divisore e mettilo sotto il secondo coefficiente. Moltiplica 1 per -2 e scrivi il prodotto -2 sotto il secondo termine, 2. Questo assomiglia a questo:

-2| 1 2 -4 8
-2
1

Immagine titolata Divide Polynomials Using Synthetic Division Step 7

7. Aggiungi il secondo coefficiente e scrivi la risposta sotto il prodotto. Ora prendi il secondo coefficiente, 2, e aggiungilo a -2. Scrivi il risultato 0 sotto i due numeri, proprio come con la divisione lunga. Ecco come appare:

-2| 1 2 -4 8
-2
1 0

Immagine titolata Divide Polynomials Using Synthetic Division Step 8

8. Moltiplica la somma per il divisore e posiziona il risultato sotto il terzo coefficiente. Ora prendi la somma, 0, e moltiplicala per il divisore, -2. Metti il risultato 0 sotto 4, il terzo coefficiente. Ecco come appare:

-2| 1 2 -4 8
-2 0
1

Immagine titolata Divide Polynomials Using Synthetic Division Step 9

9. Somma il prodotto e il terzo coefficiente e scrivi il risultato sotto il prodotto. Aggiungi 0 a -4 e scrivi la risposta -4 sotto 0. Ecco come appare:

-2| 1 2 -4 8
-2 0
1 0 -4

Immagine titolata Divide Polynomials Using Synthetic Division Step 10

10. Moltiplica questo numero per il divisore, scrivilo sotto l`ultimo coefficiente e aggiungilo al coefficiente. Ora moltiplica -4 per -2 e scrivi la risposta 8 sotto il quarto coefficiente, 8, e aggiungi questo al quarto coefficiente. 8 + 8 = 16, quindi questo è il tuo resto. Scrivi il numero sotto il prodotto. Ecco come appare:

-2| 1 2 -4 8
-2 0 8
1 0 -4 |16

Immagine titolata Divide Polynomials Using Synthetic Division Step 11

11. Posiziona ciascuno dei nuovi coefficienti accanto a una variabile con una potenza inferiore alle variabili originali. In questo caso la prima somma, è 1, e viene posta accanto ad una x elevata alla seconda potenza (1 meno di 3). La seconda somma, 0, viene posta accanto a una x, ma il risultato è 0, quindi questo termine può essere rimosso. E il terzo coefficiente, -4, diventa una costante, un numero senza variabile, perché la variabile originaria era uguale a x. Puoi scrivere una R accanto a 16, perché questo è il resto. Ecco come apparirà:

-2| 1 2 -4 8
-2 0 8
1 0 -4 |16
X + 0X - 4 R 16

X - 4R16

Immagine titolata Divide Polynomials Using Synthetic Division Step 12

12. Scrivi la risposta finale. Questo è il nuovo polinomio, x - 4, più il resto, 16 come numeratore e x + 2 come denominatore. Ecco come appare: x - 4 +16/(x +2).

Consigli

Per verificare la tua risposta, moltiplica il quoziente per il divisore e aggiungi il resto. Questo deve essere lo stesso del polinomio originale.
(divisore)(quoziente)+(resto)
(X + 2)(X - 4) + 16
Moltiplica per il primo metodo esterno, l`ultimo interno.
(X - 4X + 2X - 8) + 16
X + 2X - 4X - 8+16
X + 2X - 4X + 8