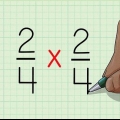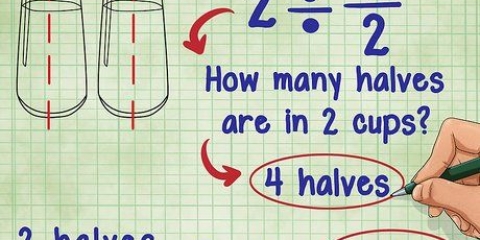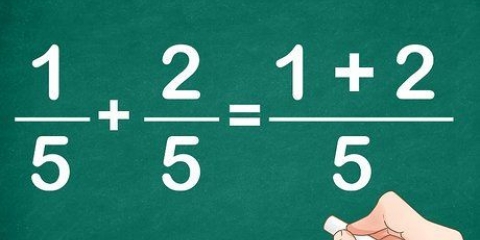Quando si tratta di due numeri pari, puoi provare a dividerli per 2 il più spesso possibile. 12/96 2/2 = 6/48 2/2 = 24/3. A quel punto potresti già essere in grado di vedere che puoi dividere 24 per 3. 24/3 3/3 = 1/8. 

Moltiplicare o dividere frazioni
Contenuto
Per moltiplicare le frazioni tutto ciò che devi fare è moltiplicare denominatori e numeratori e semplificare il risultato. Per dividere le frazioni è sufficiente invertire denominatore e numeratore di una delle frazioni e poi moltiplicare e semplificare le due frazioni. Non è difficile! Di seguito spieghiamo in passaggi come farlo.
Passi
Metodo 1 di 2: moltiplicare le frazioni

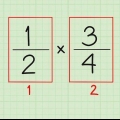
1. Moltiplica il numeratore delle frazioni. Il numeratore è il numero sopra la linea e il denominatore è il numero sotto la linea. La prima cosa da fare quando si moltiplica è affiancare le frazioni in modo che i due numeratori ei due denominatori si allineino. Se vuoi moltiplicare la frazione 1/2 per 12/48, devi prima moltiplicare i numeratori 1 e 12. 1 x 12 = 12. Scrivi il prodotto come numeratore del risultato.

2. Moltiplica il denominatore delle frazioni. Ora fai lo stesso con i denominatori. Moltiplica 2 per 48 per ottenere il nuovo denominatore. 2x48 = 96. Scrivi la risposta come denominatore del risultato. Quindi la nuova frazione è 12/96.

3. Semplifica la frazione. L`ultimo passaggio è semplificare la frazione, se possibile. Per semplificare una frazione devi trovare il massimo comun divisore (gcd) del numeratore e denominatore. Il gcd è l`intero più grande per cui entrambi gli interi possono essere divisi. Nel caso di 12 e 96 puoi dividere entrambi i numeri per 12. 12/12 = 1, 96/12 = 8. Quindi 12/96 = 1/8.
Metodo 2 di 2: Dividere le frazioni

1. Invertire numeratore e denominatore di una delle frazioni e cambiare il segno di divisione in un segno di moltiplicazione. Supponiamo di voler dividere la frazione 1/2 per 18/20. Invertire la seconda frazione per ottenere 20/18. Quindi cambi il segno di divisione in un segno di moltiplicazione. Quindi: 1/2 18/20 = 1/2 x 20/18. Non importa quale frazione inverti. 2/1 x 18/20 dà lo stesso risultato di 1/2 x 20/18.

2. Moltiplica i numeratori e denominatori delle frazioni e semplifica il risultato. Ora fai lo stesso della moltiplicazione. Per prima cosa moltiplica i numeratori 1 e 20, che diventa 20. Ora moltiplichiamo i denominatori 2 e 18. Questo dà 36 come nuovo denominatore. Quindi il prodotto delle frazioni è 20/36.Il gcd qui è 4, quindi dividi numeratore e denominatore per 4 per ottenere il risultato semplificato: 20/36 ÷ 4/4 = 5/9.
Consigli
- Controlla sempre di nuovo il tuo lavoro.
- Ricorda: puoi scrivere numeri interi come una frazione: 2 è uguale a 2/1
- Puoi sempre semplificare in modo incrociato due frazioni, se puoi. Prova a trovare il gcd del numeratore di una frazione e il denominatore dell`altra frazione (diagonale). Ad esempio: (8/20)*(6/12) può essere semplificato come segue: (2/10)*(3/3).
Avvertenze
- Fallo passo dopo passo. Allora è meno probabile che tu commetta errori.
- Semplifica sempre il più possibile.
Articoli sull'argomento "Moltiplicare o dividere frazioni"
Condividi sui social network:
Popolare