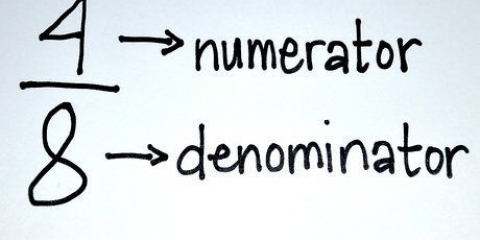
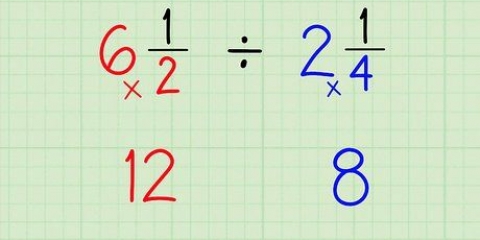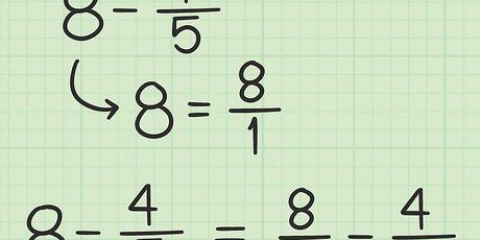18 ÷ 3 = 6, quindi 2/3 = (2x6)/(3x6)=12/18 18 ÷ 6 = 3, quindi 5/6 = (5x3)/(6x3)=15/18 18 ÷ 3 = 6, quindi 1/3 = (1x6)/(3x6)=6/18 

6/18 = (6 6)/(18 ÷ 6) = 1/3 12/18 = (12 6)/(18 ÷ 6) = 2/3 15/18 = (15 3)/(18 ÷ 3) = 5/6 La risposta è "1/3, 2/3, 5/6" 

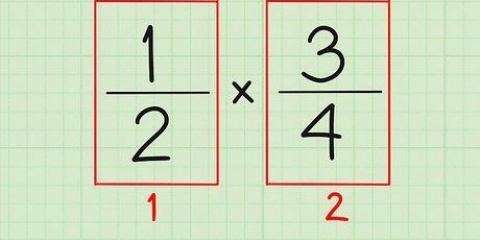
Questa è chiamata moltiplicazione incrociata, perché stai moltiplicando i numeri insieme in diagonale. 



Ricordati di posizionare sempre il prodotto della moltiplicazione accanto alla frazione di cui hai utilizzato il numeratore. 
3/5=(3x3)/(5x3)=9/15 2/3=(2x5)/(3x5)=10/15 9/15 è inferiore a 10/15 Quindi 3/5 è inferiore a 2/3 

8/3 = 2 + 2/3 9/9 = 1 19/4 = 4 + 3/4 13/6 = 2 + 1/6 
1 è il più piccolo 2 + 2/3 e 2 + 1/6 (non sappiamo ancora quale sia più grande dell`altro) 4 + 3/4 è il più grande 
2/3 = (2x2)/(3x2) = 4/6 1/6 = 1/6 4/6 è maggiore di 1/6 2 + 4/6 è maggiore di 2 + 1/6 2 + 2/3 è maggiore di 2 + 1/6 

Ordina le frazioni per dimensione
Contenuto
Sebbene sia facile ordinare numeri interi come 1, 3 e 8 per dimensione, non è sempre ovvio con le frazioni. Se ogni denominatore è uguale, puoi ordinarli come numeri interi, ad es. 1/5, 3/5 e 8/5. In altri casi puoi convertire le frazioni in modo che abbiano lo stesso denominatore, senza modificare il valore della frazione. Questo diventa più facile con la pratica e puoi usare alcuni trucchi utili, sia quando confronti due frazioni sia quando ordini frazioni in cui il numeratore è maggiore del denominatore, le frazioni improprie come 7/3.
Passi
Metodo 1 di 3: Ordinare un numero qualsiasi di frazioni

1. Trova un denominatore uguale per tutte le frazioni. Utilizzare uno dei seguenti metodi per trovare un denominatore o diminuire il numero di una frazione, che è possibile utilizzare per riscrivere ciascuna frazione nell`elenco per un facile confronto. Questo è ciò che tu chiami a Comune denominatore, o il minimo comune denominatore se questo è il più piccolo possibile:
- Moltiplica ogni denominatore insieme. Ad esempio, se stai confrontando 2/3, 5/6 e 1/3, moltiplica questi denominatori insieme: 3 x 6 = 18. Questo è un metodo semplice ma che spesso si traduce in un numero molto maggiore rispetto agli altri metodi, che sono un po` più complicati.
- o elenca i multipli di ogni denominatore in una colonna separata, finché non risalta un numero che ricorre più spesso. Ad esempio, a 2/3, 5/6 e 1/3, hai elenchi multipli di 3:3, 6, 9, 12, 15, 18. Quindi un elenco di multipli di 6: 6, 12, 18. Perché 18 si verifica in entrambi gli elenchi, usa quel numero (puoi anche usare 12, ma gli esempi seguenti presuppongono che tu usi 18).

2. Converti ogni frazione in modo che abbiano un denominatore uguale. Ricorda che se moltiplichi numeratore e denominatore di una frazione per lo stesso numero, il valore della frazione rimane lo stesso. Usa questa tecnica con ogni frazione, una alla volta, in modo che ogni frazione abbia lo stesso denominatore. Prova questo per 2/3, 5/6 e 1/3, con denominatore 18:

3. Ordina le frazioni in base ai numeratori. Ora che tutte le frazioni hanno lo stesso denominatore, sono facili da confrontare. Ordinali dal più piccolo al più grande in base al contatore. Questo ci dà il seguente elenco: 18/6, 18/12, 18/15.

4. Riporta ogni frazione alla sua forma originale. Lascia le frazioni in questo ordine, ma riconvertili nella frazione originale. Lo fai semplicemente ricordando a quale frazione appartiene a quale o dividendo nuovamente i numeri superiore e inferiore della frazione:
Metodo 2 di 3: Ordinare due frazioni con moltiplicazione incrociata

1. Scrivi le due frazioni una accanto all`altra. Ad esempio, confronta la frazione 3/5 e la frazione 2/3. Scrivili fianco a fianco: 3/5 a sinistra e 2/3 a destra.

2. Moltiplica il numeratore della prima frazione per il denominatore della seconda. Quindi: 3 x 3 = 9.

3. Scrivi la tua risposta accanto alla prima frazione. Scrivi il prodotto di 3 x 3 = 9, accanto alla prima frazione.

4. Moltiplica il numeratore di secondo frazione con denominatore di primo. Ora per vedere qual è il più grande, confrontiamo la risposta con un`altra moltiplicazione. Moltiplica questi due numeri insieme. In questo esempio (stiamo confrontando 3/5 e 2/3), stiamo moltiplicando 2 x 5.

5. Scrivi la risposta accanto alla seconda frazione. Scrivi il risultato di 2 x 5 =10 accanto alla seconda frazione.

6. Confronta i valori dei risultati. Se un valore è maggiore dell`altro, anche la frazione accanto al risultato è la più grande. Quindi, poiché 9 è inferiore a 10, 3/5 è inferiore a 2/3.

7. Come funziona esattamente? Quello che stai facendo è convertire le frazioni in modo che abbiano entrambi lo stesso denominatore. Quindi questo è ciò che fa effettivamente la moltiplicazione incrociata! Salta effettivamente annotare i denominatori perché in caso di denominatori simili devi solo confrontare i numeratori. Quindi come segue, senza il percorso breve della moltiplicazione incrociata:
Metodo 3 di 3: Ordinare frazioni maggiori di uno

1. Utilizzare questo metodo per le frazioni in cui il numeratore è maggiore del denominatore. Se il numeratore è maggiore del denominatore, allora questa frazione è maggiore di 1. 8/3 ne è un esempio. Puoi anche usarlo per frazioni con lo stesso numeratore e denominatore, come 9/9. Questi sono entrambi esempi di "improprio" frazioni.
- Puoi ancora usare gli altri metodi per queste frazioni. Questo metodo ti aiuterà a capire meglio queste frazioni e potrebbe essere un po` più veloce.

2. Converti qualsiasi frazione impropria in una frazione mista. Rendilo una combinazione di un numero intero e una frazione. A volte puoi farlo facilmente a memoria. Ad esempio, 9/9 = 1. Nei casi più complicati, usa la divisione lunga per scoprire quante volte il denominatore è divisibile per il numeratore. Qualsiasi resto della divisione lunga rimane come frazione. Ad esempio:

3. Ordina i numeri misti per il numero intero. Ora che non ci sono più frazioni improprie, hai un`idea migliore della dimensione di ciascun numero. Ignora prima le frazioni e ordina ogni numero misto in base al numero intero:

4. Confronta le frazioni in ogni gruppo, se necessario. Se hai più numeri misti con lo stesso intero, come 2 + 2/3 e 2 + 1/6, confronta la frazione di entrambi i numeri per scoprire quale è maggiore. Nell`esempio, stiamo confrontando 2 + 2/3 e 2 + 1/6, convertendo le frazioni allo stesso denominatore:

5. Utilizzare il risultato per ordinare ulteriormente l`elenco dei numeri misti. L`ordine dell`intero elenco diventa ora: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.

6. Converti i numeri misti nelle frazioni originali. Mantieni l`ordine uguale, ma annulla le modifiche e riscrivi le frazioni come frazioni improprie originali: 9/9, 3/8, 13/6, 19/4.
Consigli
- Quando si sequenziano un gran numero di frazioni, può essere utile confrontare piccoli gruppi di 2, 3 o 4 frazioni.
- Mentre trovare il minimo comune denominatore può essere utile, qualsiasi comune denominatore funzionerà. Prova a classificare 2/3, 5/6 e 1/3 con un denominatore comune di 36 e vedi se ottieni lo stesso risultato.
- Se i numeratori sono tutti uguali, puoi anche ordinare velocemente le frazioni. Ad esempio, 1/8 < 1/7 < 1/6 < 1/5. Pensa a questo come se fosse una pizza: se vai da 1/2 a 1/8, la pizza la tagli in 8 pezzi anziché in 2 e i pezzi sono più piccoli.
Articoli sull'argomento "Ordina le frazioni per dimensione"
Condividi sui social network:
Popolare