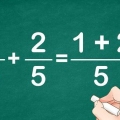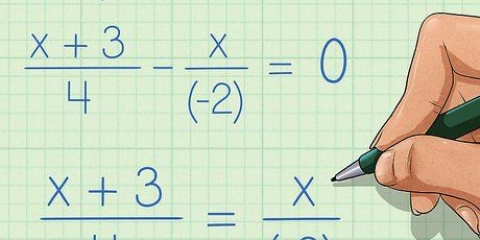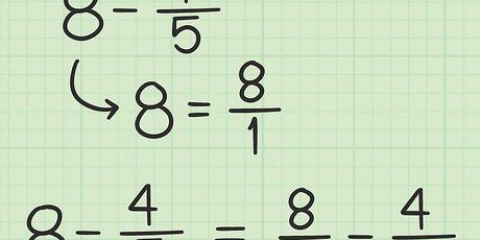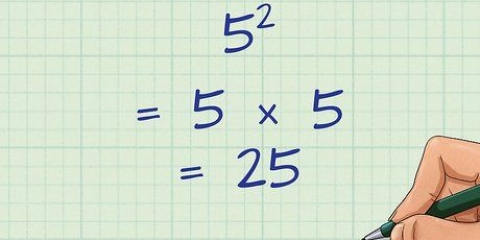Risolvere Frazioni Equivalenti: 8 Passaggi (con Immagini)

Contenuto

Passi
- Metodo 1 di 2: creazione di frazioni equivalenti
- Metodo 2 di 2: risoluzione di frazioni equivalenti con variabili
Consigli
Avvertenze

Lo sono due frazioni "equivalente" se hanno lo stesso valore. Ad esempio, le frazioni 1/2 e 2/4 sono equivalenti perché 1 su 2 ha lo stesso valore di 2 su 4 (0,5 in forma decimale). Saper convertire una frazione in un`altra, ancora equivalente, è un valore matematico essenziale di cui hai bisogno, dall`algebra di base alla matematica avanzata. Guarda il passaggio 1 per iniziare!

Passi

Metodo 1 di 2: creazione di frazioni equivalenti

Immagine titolata Do Equivalent Fractions Step 1

1. Moltiplica il numeratore e il denominatore di una frazione per lo stesso numero per ottenere una frazione equivalente. Due frazioni diverse, ma equivalenti per definizione, numeratori e denominatori multipli tra loro. In altre parole, moltiplicando numeratore e denominatore di una frazione per lo stesso numero si ottiene una frazione equivalente. Anche se i numeri in questa nuova frazione sono diversi, ha comunque lo stesso valore.

Ad esempio, se prendiamo la frazione 4/8 e moltiplichiamo sia il numeratore che il denominatore per 2, otteniamo (4×2)/(8×2) = 8/16. Queste due frazioni sono equivalenti.

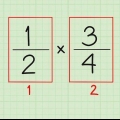
(4×2)/(8×2) è essenzialmente lo stesso di 4/8 × 2/2 Ricorda che quando moltiplichiamo due frazioni lo facciamo in questo modo: numeratore per numeratore e denominatore per denominatore. Nota che 2/2 è uguale a 1. Quindi è facile capire perché 4/8 è uguale a 8/16: la seconda frazione è la prima frazione moltiplicata per 2!

2. Dividi il numeratore e il denominatore o una frazione per lo stesso numero per ottenere una frazione equivalente. Come la moltiplicazione, anche la divisione può essere utilizzata per creare una nuova frazione equivalente alla frazione data. Basta dividere numeratore e denominatore di una frazione per lo stesso numero per ottenere una frazione equivalente. C`è un avvertimento qui: la frazione risultante deve essere composta da numeri interi sia nel numeratore che nel denominatore per essere valida.

Ad esempio, prendiamo di nuovo 4/8. Se, invece di moltiplicare, dividiamo sia il numeratore che il denominatore per 2, otteniamo (4 2)/(8 ÷ 2) = 2/4. 2 e 4 sono entrambi numeri interi, quindi questa frazione equivalente è valida.

Immagine titolata Do Equivalent Fractions Step 2

3. Semplifica la tua frazione usando il massimo comun divisore (GGD). Ogni data frazione ha un numero infinito di frazioni equivalenti: puoi moltiplicare il numeratore e il denominatore per qualsiasi numero intero, grande o piccolo per ottenere una frazione equivalente. Ma la forma più semplice di una data frazione è solitamente quella con i termini più piccoli. In tal caso, il numeratore e il denominatore sono entrambi i più piccoli possibile: non possono più essere divisi per alcun numero intero per rendere il termine ancora più piccolo. Per semplificare una frazione, dividiamo sia il numeratore che il denominatore per il massimo comun divisore.

Il massimo comun divisore (GGD) del numeratore e denominatore è il più grande intero per cui sia numeratore che denominatore sono divisibili. Quindi nel nostro esempio 4/8, perché 4 è il massimo divisore di 4 e 8, dividiamo il numeratore e il denominatore della nostra frazione per 4 per ottenere i termini più semplici. (4 4)/(8 ÷ 4) = 1/2.

Immagine titolata Do Equivalent Fractions Step 8

4. Se lo desideri, converti i numeri misti in frazioni improprie per semplificare la conversione. Naturalmente, non tutte le frazioni che incontrerai saranno facili da semplificare come 4/8. Ad esempio, numeri misti (es. 1 3/4, 2 5/8, 5 2/3, ecc.) può rendere questa conversione un po` più difficile. Se vuoi creare una frazione di un numero misto, puoi farlo in due modi: trasforma il numero misto in una frazione impropria, quindi continua, o mantieni il numero misto e fornisci un numero misto come risposta.

Per convertire una frazione impropria, moltiplica l`intero del numero misto per il denominatore della frazione, quindi aggiungi il prodotto al numeratore. Ad esempio, 1 2/3 = ((1 × 3) + 2)/3 = 5/3. Quindi puoi convertirlo di nuovo se necessario. Ad esempio, 5/3 × 2/2 = 10/6, sempre lo stesso di 1 2/3.

Tuttavia, non è necessario convertire una frazione impropria. Possiamo ignorare il numero intero e convertire semplicemente la frazione e quindi aggiungere il numero intero ad esso. Ad esempio, a 3 4/16, stiamo solo guardando 4/16. 4/16 ÷ 4/4 = 1/4. Quindi ora aggiungiamo di nuovo l`intero e otteniamo un nuovo numero misto, 3 1/4.

5. Non aggiungere o sottrarre mai per ottenere frazioni equivalenti. Quando si convertono le frazioni nella loro forma equivalente, è importante ricordare che le uniche operazioni che si applicano sono la moltiplicazione e la divisione. Non usare mai addizioni o sottrazioni. La moltiplicazione e la divisione funzionano per ottenere frazioni equivalenti perché queste operazioni sono in realtà forme del numero 1 (2/2, 3/3, ecc.) e dai risposte uguali alla frazione con cui hai iniziato. L`addizione e la sottrazione non hanno questa capacità.

Ad esempio, sopra abbiamo trovato che 4/8 ÷ 4/4 = 1/2 . Se invece avessimo aggiunto 4/4 a questo, avremmo ottenuto una risposta completamente diversa. 4/8 + 4/4 = 4/8 + 8/8 = 12/8 = 1 1/2 o 3/2, e nessuno di questi è uguale a 4/8.

Metodo 2 di 2: risoluzione di frazioni equivalenti con variabili

1. Usa la moltiplicazione incrociata per risolvere i problemi di equivalenza frazionaria. Un tipo complicato di problema di algebra che si occupa di frazioni equivalenti coinvolge equazioni con due frazioni, in cui una o entrambe contengono una variabile. In casi come questo, sappiamo che queste frazioni sono equivalenti perché sono gli unici termini su entrambi i lati del segno di uguale di un`equazione, ma non è sempre ovvio come risolvere per la variabile. Fortunatamente, possiamo moltiplicare per crosswise, risolvere questo tipo di problema senza problemi.

La moltiplicazione incrociata è esattamente come sembra: stai moltiplicando in modo incrociato sul segno di uguale. In altre parole, moltiplichi il numeratore di una frazione per il denominatore dell`altra frazione e viceversa. Quindi risolvi ulteriormente l`equazione.
Ad esempio, abbiamo l`equazione 2/x = 10/13. Ora moltiplica a croce: moltiplica 2 per 13 e 10 per x e elabora ulteriormente l`equazione:

2×13 = 26
10 × x = 10 x
10x = 26. Ora risolviamo ulteriormente l`equazione. x = 26/10 = 2.6

2. Utilizzare la moltiplicazione incrociata allo stesso modo delle equazioni multivariate o delle espressioni variabili. Una delle migliori caratteristiche della moltiplicazione incrociata è che funziona più o meno allo stesso modo sia che tu abbia a che fare con due frazioni semplici o complesse. Ad esempio, se entrambe le frazioni contengono variabili, non cambierà nulla: dovrai solo sbarazzarti di queste variabili. Allo stesso modo, se i numeratori o i denominatori della tua variabile frazione contengono espressioni, basta "continuare a moltiplicarsi" utilizzando la proprietà distributiva e risolvendo come fai di solito.

Ad esempio, supponiamo di avere l`equazione ((x + 3)/2) = ((x + 1)/4). In questo caso, lo risolviamo per moltiplicazione incrociata:

(x + 3) × 4 = 4x + 12

(x + 1) × 2 = 2x + 2

2x + 2 = 4x + 12

2 = 2x + 12

-10 = 2x

-5 = x

3. Utilizzare le tecniche per risolvere i polinomi. La moltiplicazione incrociata non funziona sempre un risultato che puoi risolvere con una semplice algebra. Se hai a che fare con termini variabili, otterrai rapidamente un`equazione quadratica o un altro polinomio come risultato. In questi casi si utilizza, ad esempio, il quadrato e/o la formula del quadrato.

Ad esempio, prendiamo l`equazione ((x +1)/3) = (4/(2x - 2)). Prima moltiplicazione incrociata:

(x + 1) × (2x - 2) = 2x + 2x -2x - 2 = 2x - 2

4×3 = 12

2x - 2 = 12. A questo punto vogliamo convertirlo in un`equazione quadratica (ax + bx + c = 0) sottraendo 12 da entrambi i membri, dando 2x - 14 = 0. Ora utilizziamo la formula (x = (-b +/- √(b - 4ac)))/2a) per trovare il valore di x:

x = (-b +/- √(b - 4ac))/2a. Nella nostra equazione, 2x - 14 = 0, a = 2, b = 0 e c = -14.

x = (-0 +/- √(0 - 4(2)(-14))))/2(2)

x = (+/- √( 0 - -112))/2(2)

x = (+/- √(112))/2(2)

x = (+/- 10.58/4)

x = +/- 2.64 A questo punto, controlliamo la nostra risposta sostituendo 2.64 e -2.64 nell`equazione quadratica originale.

Consigli

Convertire le frazioni in una forma equivalente è in realtà come moltiplicare per una frazione come 2/2 o 5/5. Poiché questo è in definitiva uguale a 1, il valore della frazione rimane lo stesso.