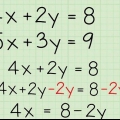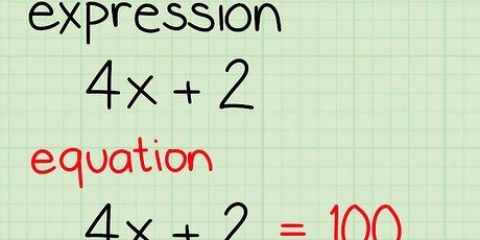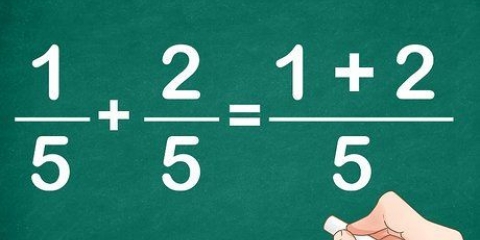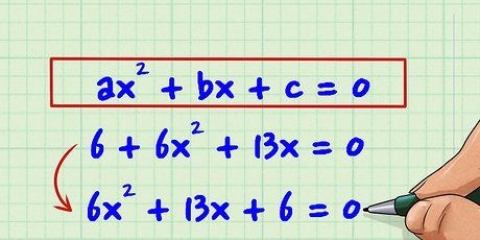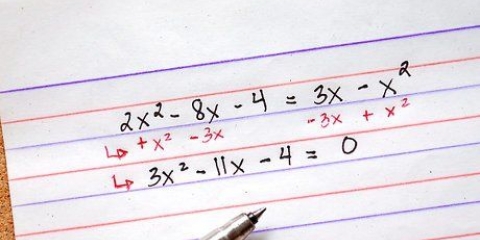Risolvere Equazioni Frazionali: 8 Passaggi (con Immagini)

Contenuto

Passi
- Metodo 1 di 2: Metodo uno: Moltiplicazione incrociata
- Metodo 2 di 2: Metodo due: Trovare il minimo comune multiplo (LCM) dei denominatori
Consigli

Una funzione razionale è una frazione con una o più variabili al numeratore o al denominatore. Un`equazione razionale è qualsiasi equazione che contiene almeno un`espressione razionale. Come le equazioni algebriche regolari, le espressioni razionali possono essere risolte applicando la stessa operazione a entrambi i lati dell`equazione fino a quando la variabile non è isolata su un lato del segno di uguale. Due metodi speciali, la moltiplicazione incrociata e la ricerca del minimo comune multiplo dei denominatori, sono particolarmente utili per isolare variabili e risolvere equazioni razionali.

Passi

Metodo 1 di 2: Metodo uno: Moltiplicazione incrociata

Immagine titolata Solve Rational Equations Step 1

1. Se necessario, riorganizzare l`equazione per assicurarsi che sia presente una frazione su entrambi i lati del segno di uguale. La moltiplicazione incrociata è un metodo rapido per risolvere le equazioni razionali. Sfortunatamente, questo metodo funziona solo per equazioni razionali che hanno esattamente un`espressione o frazione razionale su entrambi i lati del segno di uguale. Se questo non è il caso della tua equazione, allora probabilmente hai bisogno di alcune operazioni algebriche per ottenere i termini nel posto giusto.

Ad esempio, l`equazione (x + 3)/4 - x/(-2) = 0 può essere facilmente convertita nella forma corretta per la moltiplicazione incrociata aggiungendo x/(-2) a entrambi i lati dell`equazione, ottenendo il risultato appare così: (x + 3)/4 = x/(-2).

Ricorda che decimali e interi possono essere convertiti in frazioni dando loro come denominatore 1. (x + 3)/4 - 2.5 = 5, ad esempio, può essere riscritto come (x + 3)/4 = 7.5/1, che consente di applicare la moltiplicazione incrociata.

Alcune equazioni razionali non possono essere convertite così facilmente nella forma corretta. In questi casi, utilizzare i metodi che utilizzano il minimo comune multiplo dei denominatori.

Immagine titolata Solve Rational Equations Step 2

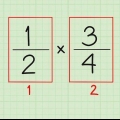
2. Moltiplicazione incrociata. La moltiplicazione incrociata significa semplicemente moltiplicare il numeratore di una frazione per il denominatore dell`altra e viceversa. Moltiplica il numeratore della frazione a sinistra del segno di uguale per la frazione a destra. Ripeti con il numeratore a destra e il denominatore della frazione a sinistra.

La moltiplicazione incrociata funziona su principi algebrici comuni. Le espressioni razionali e altre frazioni possono essere convertite in numeri ordinari moltiplicando i denominatori. La moltiplicazione incrociata è fondamentalmente un modo conveniente e abbreviato di moltiplicare entrambi i membri dell`equazione per i denominatori delle frazioni. Non ci credi? Provalo: vedrai gli stessi risultati dopo la semplificazione.

Immagine titolata Solve Rational Equations Step 3

3. Rendi i due prodotti uguali tra loro. Dopo la moltiplicazione incrociata, ti rimangono due prodotti. Rendi uguali questi due termini e semplificali per lasciare i termini più semplici su entrambi i lati dell`equazione.

Ad esempio, se (x+3)/4 = x/(-2) era la tua espressione razionale originale, dopo la moltiplicazione incrociata diventa uguale a -2(x+3) = 4x. Questo può eventualmente essere riscritto come -2x - 6 = 4x.

Immagine titolata Risolvi le equazioni razionali Step 4

4. Risolvi per la variabile. Utilizzare le operazioni algebriche per trovare il valore della variabile nell`equazione. Ricorda che se x appare su entrambi i lati del segno di uguale, devi aggiungere o sottrarre un termine x per assicurarti che ci siano solo x-termini su un lato del segno di uguale.

Nel nostro esempio, è possibile dividere entrambi i membri dell`equazione per -2, che dà usx+3 = -2x. Sottraendo x da entrambi i lati del segno di uguale si ottiene 3 = -3x. E infine, dividendo entrambi i membri per -3 otteniamo -1 = x, o anche x = -1. Ora abbiamo trovato x che risolve la nostra equazione razionale.

Metodo 2 di 2: Metodo due: Trovare il minimo comune multiplo (LCM) dei denominatori

Immagine titolata Risolvi le equazioni razionali Step 5

1. Prova a vedere quando è ovvio trovare il minimo comune multiplo dei denominatori. Il minimo comune multiplo (LCM) dei denominatori può essere utilizzato per semplificare le equazioni razionali, consentendo di trovare i valori delle loro variabili. Trovare un LCF è una buona idea se l`equazione razionale non può essere facilmente riscritta in una forma in cui c`è solo una frazione o espressione razionale su ciascun lato del segno di uguale. Per risolvere equazioni razionali con tre o più termini, gli LCF sono uno strumento utile. Ma per risolvere equazioni razionali con solo due termini, la moltiplicazione incrociata è spesso più veloce.

Immagine titolata Risolvi le equazioni razionali Step 6

2. Esamina il denominatore di ciascuna frazione. Trova il numero più piccolo divisibile per qualsiasi denominatore. Questo è il kgv della tua equazione.

A volte il minimo comune multiplo, il numero più piccolo divisibile per ciascuno dei denominatori, è immediatamente evidente. Ad esempio, se la tua espressione ha l`aspetto di x/3 + 1/2 = (3x+1)/6, è facile vedere che lcm deve essere divisibile per 3, 2 e 6, quindi è uguale a 6.

Ma più spesso l`LCF di un`equazione razionale non è affatto chiara. In questi casi, prova i multipli del denominatore più grande finché non trovi un numero che includa i multipli degli altri denominatori più piccoli. Spesso l`LCF è il prodotto di due denominatori. Ad esempio, prendi l`equazione x/8 + 2/6 = (x - 3)/9, dove lcm è uguale a 8*9 = 72.

Se uno o più denominatori contengono una variabile, questo processo è un po` più difficile, ma non è certamente impossibile. In questi casi, l`LCF è un`espressione (con variabili) in cui rientrano completamente tutti i denominatori, non solo un singolo numero. Ad esempio, l`equazione 5/(x-1) = 1/x + 2/(3x), dove lcm è uguale a 3x(x-1), perché è completamente divisibile per qualsiasi denominatore – dividendo per(x - 1) dà 3x, la divisione per 3x dà (x-1) e la divisione per x dà 3(x-1).

Immagine titolata Solve Rational Equations Step 7

3. Moltiplica ogni frazione dell`equazione razionale per 1. Moltiplicare qualsiasi termine per 1 può sembrare inutile, ma qui c`è un trucco. 1 può essere scritto come una frazione, ad es. 2/2 e 3/3. Moltiplica ogni frazione nella tua equazione razionale per 1, scrivendo 1 ogni volta che il numero o il termine moltiplicato per ciascun denominatore per rappresentare l`LCF come frazione.

Nel nostro esempio, possiamo moltiplicare x/3 per 2/2 per ottenere 2x/6 e moltiplicare 1/2 per 3/3 per ottenere 3/6. 3x +1/6 ha già un 6 (LCM) come denominatore, quindi possiamo moltiplicarlo per 1/1 o semplicemente lasciarlo da solo.

Nel nostro esempio con le variabili ai denominatori, l`intero processo è un po` più complicato. Poiché lcc è uguale a 3x(x-1) moltiplichiamo qualsiasi espressione razionale per una frazione che produce 3x(x-1) come denominatore. Moltiplichiamo 5/(x-1) per (3x)/(3x) e questo dà 5(3x)/(3x)(x-1), moltiplichiamo 1/x per 3(x-1)/3(x -1) e questo dà 3(x-1)/3x(x-1) e moltiplichiamo 2/(3x) per (x-1)/(x-1) e questo alla fine dà 2(x-1)/ 3x(x-1).

Immagine titolata Solve Rational Equations Step 8

4. Semplifica e risolvi per x. Ora che ogni termine nella tua equazione razionale ha lo stesso denominatore, è possibile rimuovere i denominatori dall`equazione e risolvere per i numeratori. Basta moltiplicare entrambi i membri dell`equazione per lcg per eliminare i denominatori in modo da rimanere solo con i numeratori. Ora è diventata un`equazione regolare che puoi risolvere per la variabile isolandola su un lato del segno di uguale.

Nel nostro esempio, dopo aver moltiplicato, puntando 1 come frazione, otteniamo 2x/6 + 3/6 = (3x+1)/6. Si possono sommare due frazioni se hanno lo stesso denominatore, quindi possiamo scrivere questa equazione come (2x+3)/6 = (3x+1)/6 senza cambiarne il valore. Moltiplica entrambi i membri per 6 per annullare i denominatori, lasciandoci con 2x+3 = 3x+1. Qui sottrarre 1 da entrambi i lati per ottenere 2x+2 = 3x e sottrarre 2x da entrambi i lati per ottenere 2 = x, che può anche essere scritto come x = 2.

Nel nostro esempio con variabili ai denominatori, l`equazione dopo aver moltiplicato ogni termine per "1" uguale a 5(3x)/(3x)(x-1) = 3(x-1)/3x(x-1) + 2(x-1)/3x(x-1). Moltiplicando ogni termine per lcm si possono eliminare i denominatori, ottenendo 5(3x) = 3(x-1) + 2(x-1). Questo è ulteriormente elaborato come 15x = 3x - 3 + 2x -2, che può essere ulteriormente semplificato come 15x = x - 5. Sottraendo x da entrambi i lati si ottiene 14x = -5, che può semplificare la risposta finale a x = -5/14.

Consigli

Una volta trovato il valore della variabile, controlla la tua risposta inserendo questo valore nell`equazione originale. Una volta ottenuto il valore corretto della variabile, dovresti essere in grado di semplificare l`equazione in un teorema semplice e valido, come 1 = 1.
Ogni equazione può essere scritta come un`espressione razionale; mettilo come numeratore sopra il denominatore 1. Quindi l`equazione x+3 può essere scritta come (x+3)/1, entrambi hanno lo stesso valore.