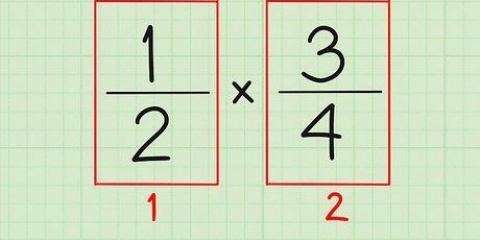
Esempio: x - 25 = (x+5)(x-5) 

Semplificare le frazioni matematiche
Contenuto
Le frazioni matematiche o algebriche all`inizio sembrano incredibilmente difficili e possono sembrare scoraggianti da affrontare per lo studente non addestrato. Con una combinazione di variabili, numeri e persino esponenti è difficile sapere da dove cominciare. Ma fortunatamente, le stesse regole necessarie per semplificare le frazioni comuni, come 15/25, si applicano anche alle frazioni matematiche.
Passi
Metodo 1 di 3: Semplificare le frazioni

1. Conoscere il vocabolario delle frazioni matematiche. I seguenti termini verranno utilizzati negli esempi e sono comuni nei problemi con le frazioni:
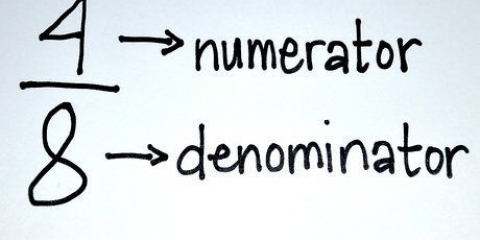
- Contatore: La parte superiore di una frazione (es. (x+5)/(2x+3)).
- Denominatore: La parte inferiore di una frazione (es. (x+5)/(2x+3)).
- Comune denominatore: Questo è un numero per il quale puoi dividere sia il numeratore che il denominatore di una frazione. Ad esempio, nella frazione 3/9, il comun divisore è 3, poiché entrambi i numeri possono essere divisi per 3.
- Fattore:` Un numero che viene moltiplicato per formare un altro numero. Ad esempio: i fattori di 15 sono 1, 3, 5 e 15. I fattori di 4 sono 1, 2 e 4.
- Equazione semplificata: Tutti i fattori comuni vengono rimossi e le variabili uguali vengono raggruppate (5x + x = 6x) fino a ottenere la forma più semplice di frazione, equazione o problema. Se non puoi più fare nulla con la frazione, è semplificato.

2. Confronta come risolvere le frazioni semplici. Questi sono esattamente gli stessi passaggi che farai per risolvere le frazioni matematiche. Prendi l`esempio, 15/35. Per semplificare una frazione, abbiamo bisogno trovare un denominatore comune. In questo caso, entrambi i numeri possono essere divisi per cinque, quindi puoi cancellare il 5 dalla frazione:
15→5*3
35→5 *7
Ora puoi cancella come termini. In questo caso, puoi cancellare i due cinque, lasciando la tua risposta semplificata, 3/7.
35→5 *7
Ora puoi cancella come termini. In questo caso, puoi cancellare i due cinque, lasciando la tua risposta semplificata, 3/7.

3. Rimuovere i fattori dalle espressioni algebriche proprio come i normali numeri. Nell`esempio precedente, potresti facilmente rimuovere 5 da 15 e lo stesso principio si applica a espressioni più complesse come 15x - 5. Trova un fattore che entrambi i numeri hanno in comune. Qui la risposta è 5, perché puoi dividere sia 15x che -5 per il numero cinque. Come prima, rimuovi il fattore comune e lo moltiplichi per ciò che è "rimasto".`
15x - 5 = 5 *(3x - 1) Per controllare il tuo lavoro, moltiplica nuovamente i cinque nella nuova espressione: ti ritroverai con gli stessi numeri con cui hai iniziato.

4. Ora puoi eliminare i termini complessi proprio come i termini semplici. Lo stesso principio delle frazioni regolari funziona anche per le frazioni matematiche. Questo è il modo più semplice per semplificare le frazioni. Prendi la frazione:
(x+2)(x-3)
(x+2)(x+10)
Nota come il termine (x+2) compare sia al numeratore (in alto) che al denominatore (in basso). Pertanto, puoi rimuoverli per semplificare la frazione algebrica, proprio come hai rimosso il 5 da 15/35:
(x+2)(x-3)→(x-3)
(x+2)(x+10)→(x+10)
(x+2)(x+10)
Nota come il termine (x+2) compare sia al numeratore (in alto) che al denominatore (in basso). Pertanto, puoi rimuoverli per semplificare la frazione algebrica, proprio come hai rimosso il 5 da 15/35:
Metodo 2 di 3: Semplificare le frazioni

1. Trova un fattore comune nel numeratore (la parte superiore della frazione). La prima cosa da fare quando si semplifica una frazione algebrica è semplificare ogni parte della frazione. Inizia con la parte superiore e cancella quanti più numeri possibili. Come esempio useremo questo esercizio:
9x-3
15x+6
Inizia con il contatore: 9x – 3. C`è un fattore comune sia per 9x che per -3, che è 3. Lavora le 3 parentesi esterne come faresti con qualsiasi altro numero, lasciando 3*(3x-1). Questo è il tuo nuovo contatore:
3(3x-1)
15x+6
15x+6
Inizia con il contatore: 9x – 3. C`è un fattore comune sia per 9x che per -3, che è 3. Lavora le 3 parentesi esterne come faresti con qualsiasi altro numero, lasciando 3*(3x-1). Questo è il tuo nuovo contatore:
15x+6

2. Trova un fattore comune al denominatore.Continuando l`esempio sopra, isolare il denominatore, 15x+6. Cerca di nuovo un numero che si adatti a entrambe le parti. Anche qui puoi omettere un fattore tre, in modo da rimanere con 3 *(5x +2). Incorpora il tuo nuovo denominatore nell`equazione:
3(3x-1)
3(5x+2)
3(5x+2)

3. Rimuovi i termini simili. Questa è la fase in cui puoi davvero semplificare la frazione. Prendi tutti i termini che sono sia al numeratore che al denominatore e rimuovili. In questo caso possiamo barrare i 3 sia dall`alto che dal basso.
3(3x-1)→(3x-1)
3(5x+2)→(5x+2)

4. Sapere quando l`equazione è completamente semplificata. Una frazione è semplificata quando non ci sono più fattori comuni in alto o in basso. Ricorda, non puoi rimuovere i fattori all`interno delle parentesi - nel problema di esempio, non puoi fattorizzare x di 3x e 5x, perché i termini completi sono in realtà (3x -1) e (5x + 2). Quindi l`esempio è completamente semplificato, con if la risposta finale:
(3x-1)
(5x+2)
(5x+2)

5. Prova un esercizio pratico. Il modo migliore per imparare è continuare a cercare di semplificare le frazioni matematiche. Le risposte sono sotto i problemi.
4(x+2)(x-13)
(4x+8) Risposta: (x=13)
2x-x
5 volte Risposta:(2x-1)/5
(4x+8)
5 volte
Metodo 3 di 3: Trucchi per risolvere problemi più complicati

1. `Inverti` le frazioni per fattorizzare con numeri negativi. Diciamo di avere la seguente equazione:
3(x-4)
5(4-x)
Nota come (x-4) e (4-x) quasi sono identici, ma non puoi cancellarli perché sono invertiti. Tuttavia, (x - 4) può essere scritto come -1 *(4 - x) nello stesso modo in cui riscrivi (4 + 2x) come 2 *(2 + x). Questo si chiama `portare fuori dalla parentesi`.
-1*3(4-x)
5(4-x)
Ora possiamo semplicemente omettere i due identici (4-x):
-1*3(4-x)
5(4-x)
Da ciò segue la risposta finale: -3/5
5(4-x)
Nota come (x-4) e (4-x) quasi sono identici, ma non puoi cancellarli perché sono invertiti. Tuttavia, (x - 4) può essere scritto come -1 *(4 - x) nello stesso modo in cui riscrivi (4 + 2x) come 2 *(2 + x). Questo si chiama `portare fuori dalla parentesi`.
5(4-x)
Ora possiamo semplicemente omettere i due identici (4-x):
5
Da ciò segue la risposta finale: -3/5

2. Riconosci la differenza di due quadrati mentre lavori. La differenza di due quadrati sta semplicemente sottraendo un numero al quadrato da un altro, come l`espressione (a - b). La differenza dei quadrati perfetti è sempre semplificata in due parti, aggiungendo e sottraendo le radici quadrate. In ogni caso, puoi semplificare la differenza dei quadrati perfetti in questo modo:
a - b = (a+b)(a-b) Questo può essere molto utile quando si cerca di trovare termini simili nelle frazioni matematiche.

3. semplificare i polinomi. I polinomi o polinomi sono espressioni algebriche complesse con più di due termini, come ad esempio: x + 4x + 3. Fortunatamente, molti polinomi possono essere semplificati `fattorizzazione`. L`espressione precedente, ad esempio, può essere riscritta come (x+3)(x+1).

4. Ricorda che le variabili possono anche essere fattorizzate. Ciò è particolarmente utile per le espressioni con esponenti, come x + x. Puoi omettere l`esponente più grande come fattore. In questo caso: x + x = x(x + 1).
Consigli
- Controlla il tuo lavoro sulla fattorizzazione moltiplicando il fattore nell`equazione: otterrai lo stesso numero con cui hai iniziato.
- Elimina sempre i numeri più grandi che puoi per semplificare completamente la tua equazione.
Avvertenze
- Non dimenticare le regole di calcolo (ordine delle operazioni), altrimenti le cose andranno male. Pertanto, imparalo nel miglior modo possibile.
Articoli sull'argomento "Semplificare le frazioni matematiche"
Condividi sui social network:
Popolare