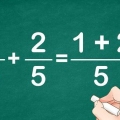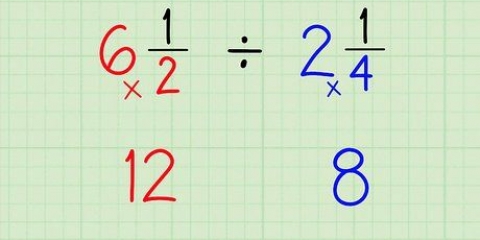Ad esempio: nella frazione 1/5, 1 è il numeratore. 
Ad esempio: nella frazione 1/5, 5 è il denominatore, quindi la frazione è composta da cinque parti. 
Ad esempio: 3/4 è una frazione reale e 5/3 è una frazione impropria. Se hai un numero intero con una frazione, si chiama frazione mista. Ad esempio: 1 1/2 è una frazione mista. 

Ad esempio, per trovare un fattore comune per 1/3 + 2/5, moltiplica 1 e 3 per 5 e moltiplica 2 e 5 per 3. Quindi ottieni 5/15 + 6/15. Ora puoi sommare le frazioni. 
Ad esempio: 3/6 - 2/6=1/6. Non sommare (o sottrarre) i denominatori. 


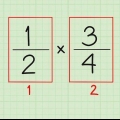
Ad esempio, per moltiplicare 1/3 per 3/4, moltiplicare 1 per 3 per ottenere il numeratore. Quindi moltiplica 3 per 4 per ottenere il denominatore. La tua risposta è quindi 3/12. 
Ad esempio, se la tua risposta è 3/12, allora 3 è il massimo comun divisore. Semplifica la frazione di 3 per ottenere 1/4. 

Per continuare con l`esempio, moltiplica 5/4 per 2/1 per ottenere 10/4. 
Ad esempio, il massimo comun divisore per 10/4 è 2, quindi la tua risposta semplificata è 5/2. Se questa è una frazione impropria, rendila un numero intero con una frazione. 5/2 diventa quindi 2 1/2.
Calcolo con le frazioni
Contenuto
Il conteggio con le frazioni è una delle abilità matematiche più utili da sviluppare. Prima di iniziare, impara a riconoscere le diverse parti e tipi di frazioni. Quindi puoi continuare ad aggiungere e sottrarre frazioni. Potresti trovare più difficile moltiplicarli e dividerli. Nella maggior parte dei casi dovrai anche semplificare o ridurre la frazione.
Passi
Metodo 1 di 4: identificare le parti di una frazione

1. fare una frazione. Le frazioni sono scritte come due numeri uno sotto l`altro, separati da un trattino.

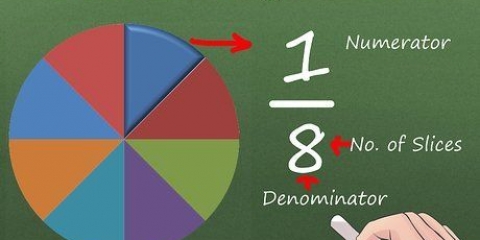
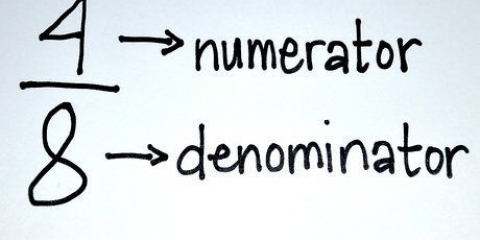
2. Trova il contatore. Il numero in alto si chiama numeratore e ti dice quante parti della frazione ci sono.

3. Trova il denominatore. Il numero sotto la barra di divisione è chiamato denominatore. Questo numero indica che tipo di frazione è.

4. Determina se la frazione è reale (effettiva) o falsa (impropria). Se il numeratore è minore del denominatore, la frazione è reale. In una frazione impropria, il numeratore è maggiore del denominatore.
Metodo 2 di 4: addizione o sottrazione di frazioni

1. Riconosci le frazioni con denominatori simili. Se devi sommare o sottrarre frazioni, devono avere denominatori comuni prima di eseguire i calcoli. Guarda il denominatore di ogni frazione per vedere se sono uguali (comuni).

2. Trova un denominatore comune se i denominatori sono diversi. Se i denominatori non sono gli stessi, devi cambiare le frazioni in modo che abbiano gli stessi denominatori. Per trovare un denominatore comune, moltiplica il numeratore e il denominatore di una frazione per il denominatore dell`altra frazione.

3. Calcola la frazione aggiungendo o sottraendo. Una volta trovato un denominatore comune e moltiplicato i numeri secondo necessità, sei pronto per sommare o sottrarre le frazioni. Somma o sottrai i numeratori e metti la somma sopra una divisione. Metti il denominatore comune sotto la linea di divisione.

4. Se necessario semplificare la somma. Se dovessi trovare un denominatore comune, potresti ritrovarti con una grande frazione che può essere semplificata. Ad esempio, se aggiungi 8/32 +12/32, ottieni 20/32. Questo può essere semplificato a 5/8.
Metodo 3 di 4: Moltiplicare e semplificare le frazioni

1. Converti frazioni miste o interi in frazioni improprie. Per rendere più facile la moltiplicazione, dovresti lavorare con frazioni reali o improprie. Se hai un numero intero o una frazione mista che vuoi moltiplicare, trasformalo in una frazione.
- Ad esempio, per moltiplicare 2/5 per 7, faresti 7 una frazione. Quindi puoi moltiplicare 2/5 per 7/1.
- Se hai una frazione mista come 1 1/3, rendila una frazione impropria (4/3) prima di moltiplicare.

2. Moltiplica i numeratori e denominatori. Invece di sommare i numeratori, moltiplicali insieme e scrivi il risultato sopra una linea di divisione. Devi anche moltiplicare i denominatori e mettere il risultato sotto la linea di divisione.

3. Semplifica il risultato. In molti casi dovrai ridurre il risultato a una frazione semplificata, soprattutto se hai iniziato con frazioni improprie. Trova il massimo comun divisore e usalo per semplificare numeratore e denominatore.
Metodo 4 di 4: Dividere le frazioni

1. Invertire la seconda frazione. Il modo più semplice per dividere le frazioni, anche quelle con denominatore diverso, è capovolgere la seconda frazione prima di calcolare la somma.
- Ad esempio: con 5/4 ÷ 1/2 devi capovolgere 1/2 a 2/1.

2. Moltiplica i numeratori e denominatori. Moltiplica le frazioni (non incrociate) per moltiplicare i numeratori. Metti il risultato sopra la divisione frazionaria e moltiplica i denominatori. Metti il risultato sotto la linea di divisione.

3. Semplifica i risultati, se necessario. Se la tua risposta è una frazione impropria o può essere semplificata, semplifica la frazione. Usa il massimo comun divisore per semplificare la frazione.
Consigli
- Se stai lavorando con frazioni impilate, dovrai eseguire alcuni passaggi aggiuntivi per ottenerle semplificarli, ma resta una parte necessaria dell`elaborazione.
- Annota sempre le tue frazioni in modo ordinato per ridurre la possibilità di errori di calcolo.
Articoli sull'argomento "Calcolo con le frazioni"
Condividi sui social network:
Popolare