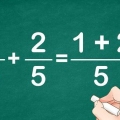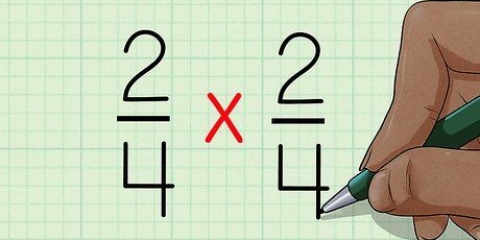Il reciproco di 3/4 è 4/3. Il reciproco di 7/5 è 5/7. Il reciproco di 1/2 è 2/1 e quindi 2. 
Lascia il contatore invariato. Fai del segno di divisione una moltiplicazione. Fai l`inverso della seconda frazione. Moltiplica i numeratori delle due frazioni. Il risultato sarà il contatore della tua risposta. Moltiplica i denominatori delle due frazioni. Il risultato sarà il denominatore della tua risposta. Semplifica la frazione. 
1/3 ÷ 2/5 = sta diventando: 1/3 * __ = Ora ruotiamo la seconda frazione (2/5). Questo diventa quindi 5/2: 1/3 * 5/2 = Ora moltiplichiamo i numeratori delle due frazioni, 1*5 = 5. 1/3 * 5/2 = 5/ Ora moltiplichiamo i denominatori delle due frazioni, 3*2 = 6. Ora abbiamo: 1/3 * 5/2 = 5/6 Questa particolare frazione non può essere ulteriormente semplificata, quindi ora abbiamo la nostra risposta. 



2/3 * 7/3 = __ 

Condividi prima il contatore 14 per mezzo di 9.9 va in 14 una volta, con un resto di 5, quindi puoi scriverlo come: 1 5/9. Puoi fermarti ora, perché hai trovato la risposta! Puoi vedere che questa frazione non può essere ulteriormente semplificata, perché 9 non è completamente divisibile per 5 e perché il numeratore è un numero primo. 
Per prima cosa dividi il numeratore per il denominatore, (24/10 = 2 resto 4). Scrivi la risposta come 2 4/10. Ma possiamo semplificare ulteriormente questa frazione! Nota che 4 e 10 sono entrambi numeri pari, quindi il primo passo è semplificare dividendo entrambi per 2.La frazione ora è 2/5. Poiché il denominatore (5) non rientra completamente nel numeratore (2) ed è anche primo, sai che non puoi semplificare ulteriormente questa frazione. Quindi la risposta è: 2 2/5. 
Dividendo le frazioni per le frazioni
Contenuto
Dividere una frazione per una frazione può sembrare confuso all`inizio, ma in realtà è davvero semplice. Tutto quello che devi fare è invertire la parte inferiore o la seconda frazione, quindi moltiplicare entrambe le frazioni insieme! Questo articolo ti mostrerà come farlo e ti mostrerà che dividere le frazioni per frazioni non dovrebbe essere affatto un problema.
Passi
Parte 1 di 2: Capire come funziona

1. Pensa a cosa significa dividere per una frazione.L`esercizio 2 ÷ 1/2 dice lo stesso di: "Quante volte ½ va in 2?”La risposta è 4, perché puoi dividere 2 in 4 mezzi pezzi.
- Prova anche a pensare a questo problema in termini di bicchieri d`acqua: quanti mezzi bicchieri d`acqua ci sono in 2 bicchieri d`acqua?? Puoi risolvere questo problema versando 2 mezzi bicchieri d`acqua in un altro bicchiere, in modo da avere alla fine 2 bicchieri pieni d`acqua: 2 mezzo/1 bicchiere * 2 bicchieri = 4 mezzi bicchieri.
- Ciò significa che se dividi un numero per un numero compreso tra 0 e 1, la risposta sarà sempre maggiore di quel numero! Questo è vero se dividi un numero intero o una frazione per un`altra frazione.

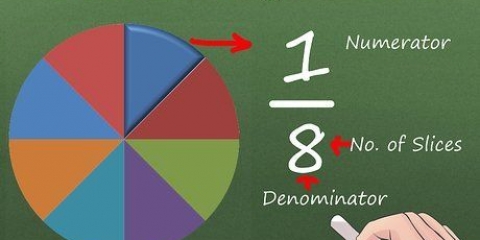
2. La divisione è l`opposto della moltiplicazione.Quindi puoi anche pensare di dividere per una frazione moltiplicando per il reciproco di quella frazione.L`inverso di una frazione è ciò che dice, semplicemente scambiando numeratore e denominatore. Tra un momento divideremo le frazioni per frazioni moltiplicando per il reciproco del denominatore, ma per ora vedremo alcuni reciproci di frazioni:

3. Ricorda i seguenti passaggi per dividere una frazione per un`altra frazione.Ecco i passaggi in ordine:

4. Esegui questi passaggi nell`esempio 1/3 ÷ 2/5.Lasciamo invariato il numeratore (la prima frazione) e cambiamo il segno di divisione in un segno di tempi:

5. Prova a ricordare quanto segue:"Dividere per una frazione equivale a moltiplicare per il reciproco."
Parte 2 di 2: Dividere le frazioni per le frazioni - esempi

1. Inizia con un problema di esempio. Supponiamo di avere il compito 2/3 3/7. La domanda qui è quanto spesso 3/7 si adatta a 2/3. Niente panico; non è così difficile come sembra!

2. Trasforma il segno di divisione in un segno di moltiplicazione. Il compito ora diventa: 2/3 * __ (riempiremo il campo vuoto tra un momento.)

3. Ora determiniamo il reciproco della seconda frazione.Ciò significa che capovolgiamo 3/7 in modo che il numeratore diventi 3 e il denominatore diventi 7.Il reciproco di 3/7 è 7/3.Ora scriviamo il nuovo problema:

4. Moltiplica le frazioni.Innanzitutto moltiplichiamo i numeratori delle due frazioni: 2 * 7 = 14.14 è il numeratore della tua risposta.Quindi moltiplichiamo insieme i denominatori delle due frazioni:3 * 3 = 9.9 è il denominatore della tua risposta.Ora lo sai 2/3 * 7/3 = 14/9.

5. Semplifica la frazione.In questo caso, poiché il numeratore della frazione è maggiore del denominatore, sappiamo che la frazione è maggiore di 1 e dobbiamo convertirla in un numero misto.(Un numero misto è un numero intero con una frazione, ad esempio 1 2/3.)

6. Proviamo un altro esempio!Supponiamo di avere il seguente problema 4/5 2/6 =.Innanzitutto, cambia il segno di divisione in un segno di moltiplicazione (4/5 * __ =), quindi trova il reciproco di 2/6, che è 6/2.Ora il compito è il seguente: 4/5 * 6/2 =__.Ora moltiplichiamo i numeratori, 4 * 6 = 24, e i denominatori 5*2 = 10.Ora abbiamo quanto segue:4/5 * 6/2 = 24/10.Semplifica la frazione. Poiché il numeratore è maggiore del denominatore, dovremo convertirlo in una frazione mista.

7. Scopri di più sulla semplificazione delle frazioni. Potresti aver imparato tutto questo una volta, ma non fa mai male rinnovare ancora una volta tutta quella conoscenza perduta. Vari articoli possono essere trovati su Internet per migliorare nuovamente queste abilità.
Articoli sull'argomento "Dividendo le frazioni per le frazioni"
Condividi sui social network:
Popolare