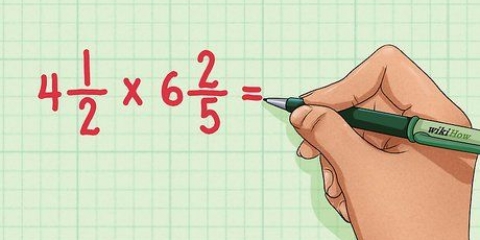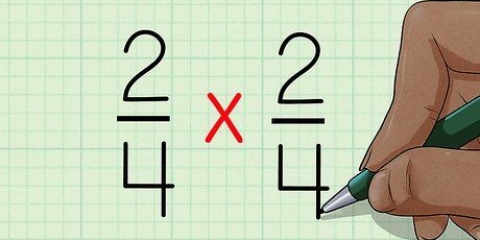Dividere una Frazione per un Numero Intero: 7 Passaggi (con Immagini)

Contenuto

Passi
Consigli
Avvertenze

Dividere le frazioni per un numero intero non è così difficile come sembra. Per dividere una frazione per un numero intero, tutto ciò che devi fare è fare una frazione del numero intero, trovare il reciproco della frazione e quindi moltiplicare il risultato per la prima frazione. Se vuoi sapere come farlo, segui questi passaggi:

Passi

Immagine titolata Dividi le frazioni per un numero intero Passaggio 1

1. Annota la somma. Il primo passo per dividere una frazione per un numero intero è scrivere la frazione, seguita dal segno di divisione e il numero intero necessario per dividerlo. Diciamo di dover risolvere la seguente somma: 2/3 ÷ 4.

Immagine titolata Dividi le frazioni per un numero intero Passaggio 2

2. Fai una frazione del numero intero. Per trasformare il numero intero in una frazione, tutto ciò che devi fare è mettere il numero 1 sotto di esso. Il numero intero diventa il numeratore e 1 diventa il denominatore della frazione. 4/1 è uguale a 4, perché stai solo mostrando che hai 4 volte il numero "1" si intende.Quindi ora la somma diventa 2/3 ÷ 4/1.

Immagine titolata Dividi le frazioni per un numero intero Passaggio 3

3. Dividere una frazione per un`altra frazione equivale a moltiplicare quella frazione per il reciproco dell`altra frazione.

Immagine titolata Dividi le frazioni per un numero intero Step 4

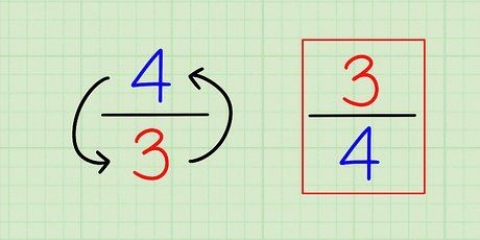
4. Scrivi il reciproco del numero intero. Per trovare il reciproco di un numero, è sufficiente invertire numeratore e denominatore. Quindi il reciproco di 4/1 è 1/4.

Immagine titolata Dividi le frazioni per un numero intero Passaggio 5

5. Cambia il segno di divisione in segno di moltiplicazione. La somma ora diventa 2/3 x 1/4.

Immagine titolata Dividi le frazioni per un numero intero Passaggio 6

6. Moltiplica insieme numeratori e denominatori della frazione. Il prossimo passo è moltiplicare i numeratori e denominatori della frazione per ottenere il nuovo numeratore e denominatore della risposta finale.

Per moltiplicare i numeratori fai 2 x 1, quindi ottieni 2.

Per moltiplicare i denominatori, fai 3 x 4, quindi ottieni 12.

2/3 x 1/4 = 2/12

Immagine titolata Dividi le frazioni per un numero intero Passaggio 7

7.Semplifica la frazione. Per semplificare la frazione, è necessario il massimo comun divisore (ggd) trova. Il gcd è il numero più grande per cui due numeri, in questo caso il numeratore e il denominatore, sono divisibili. Poiché il numeratore è 2, devi vedere se 12 è divisibile per 2 -- e lo è, perché 12 è un numero pari. Dividi sia il numeratore che il denominatore per 2 per ottenere il nuovo numeratore e denominatore, quindi hai semplificato la frazione.

2 2 = 1

12÷2 = 6

Puoi semplificare la frazione da 2/12 a 1/6. Questa è la tua risposta finale.

Consigli

Ecco un mnemonico per una facile memorizzazione: "Dividere per una frazione = moltiplicare per il reciproco!"
Puoi anche prima, cioè prima di moltiplicare, barrare i numeri uno contro l`altro, quindi non devi cercare il gcd alla fine. Nel nostro esempio, prima di moltiplicare 2/3 × 1/4, possiamo vedere che il primo numeratore (2) e il secondo denominatore (4) corrispondono al fattore 2. Se ora ci annulliamo a vicenda, otteniamo 1/3 × 1/2 e ora il risultato è immediatamente 1/6.
Il metodo funziona ancora se una delle frazioni è negativa, ma tieni d`occhio il segno meno mentre segui i passaggi. Tieni presente che in una frazione, il meno appartiene al numeratore.
Cancella i numeri prima di moltiplicare, invece di semplificare alla fine.

Avvertenze

Girare solo il secondo frazione al passaggio 3. Non modificare la prima frazione. Nel nostro esempio cambiamo 4/1 in 1/4, ma lasciamo intatto 2/3 (non lo cambiamo in 3/2).