Nota che se al momento non esiste un multiplo comune, devi continuare fino a trovare un multiplo valido per entrambi i denominatori. Esempio: 2 *15=30; 3 *10=30; 5 *6=30 Il kgv=30 
Esempio: 15 *(1/2); 10 *(1/3); 6 *(1/5) Nuova somma: 30/15 + 30/10 + 30/6 
Esempio: 15/30 + 10/30 + 6/30=31/30=1 1/30 

Nel nostro esempio, 8 e 12 condividono il denominatore 1, 2 e 4. Il massimo comun divisore è 4. 
Esempio: 8 *12=96 
Esempio: 96 / 4=24 
Esempio: 24 / 8=3; 24 / 12=2 3 *(3/8)=9/24; 2 *(5/12)=10/24 24/9 + 24/10 
Esempio: 24/9 + 24/10=24/19 

Esempio: ce ne sono due 2-e in 4; zero 2-e in 5; Due 2-e nel 12 Ci sono zero 3-e in 4 e 5; un 3 nel 12 Ci sono zero 5-e in 4 e 12; un 5 in 5 
Esempio: il numero più grande per 2 è due; il maggior numero per 3 è un; il maggior numero per 5 è un. 
Esempio: 2, 2, 3, 5 
Esempio: 2 *2 *3 *5=60 kgf=60 
Esempio: 60/4=15; 60/5=12; 60/12=5 15 *(1/4)=15/60; 12 *(1/5)=12/60; 5 *(1/12)=5/60 15/60 + 12/60 + 5/60 
Esempio: 15/60 + 12/60 + 5/60=32/60=8/15 

Nota che non devi elencare multipli di 1 perché ogni numero è un multiplo di 1. Esempio: 4 *1=4; 4 *2=8; 4 *3=12; 4 *4=16; eccetera. 3 *1=3; 3 *2=6; 3 *3=9; 3 *4=12; eccetera. Il kgv=12 
Esempio: 12 *(8/1)=96/12; 3 *(9/4)=27/12; 4 *(2/3)=8/12 96/12 + 27/12 + 8/12 
Esempio: 96/12 + 27/12 + 8/12=131/12=10 11/12
Trova il minimo comune multiplo di due denominatori
Contenuto
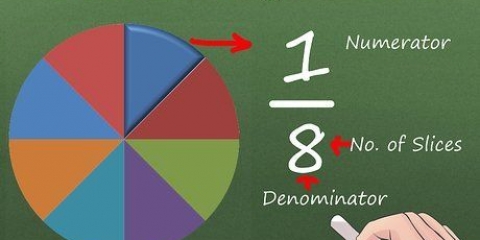
Per sommare o sottrarre frazioni con denominatori diversi. è necessario prima trovare il minimo comune multiplo di questi due numeri. Questo è il multiplo più piccolo di qualsiasi denominatore in un`equazione. Ecco alcuni metodi diversi che puoi utilizzare per trovare lcm e usarli per risolvere i problemi di frazione.
Passi
Metodo 1 di 4: elenca i multipli

1. Elenca i multipli di ogni denominatore. Ogni lista dovrebbe essere composta dal denominatore della frazione moltiplicato per 1, 2, 3, 4 e così via.
- Esempio: 1/2 + 1/3 + 1/5
- Multipli di 2: 2 *1=2; 2 *2=4; 2 *3=6; 2 *4=8; 2 *5=10; 2 *6=12; 2 *7=14; eccetera.
- Multipli di 3: 3 *1=3; 3 *2=6; 3 *3=9; 3 *4=12; 3 *5=15; 3 *6=18; 3 *7=21; eccetera.
- Multipli di 5: 5 *1=5; 5 *2=10; 5 *3=15; 5 *4=20; 5 *5=25; 5 *6=30; 5 *7=35; eccetera.

2. Trova il minimo comune multiplo. Scorri ogni elenco ed evidenzia qualsiasi multiplo comune di entrambi i denominatori. Dopo aver determinato i multipli comuni, determinare qual è il più piccolo.

3. Riscrivi il problema originale. Per scrivere ogni frazione di questa somma in modo che abbia lo stesso valore del problema originale, è necessario moltiplicare il numeratore e il denominatore della frazione per il valore appropriato, che corrisponde al multiplo comune trovato.

4. Risolvere. Dopo aver trovato l`LCF e le frazioni sono state modificate, dovresti essere in grado di risolvere questo problema senza alcun problema.
Metodo 2 di 4: utilizzo del massimo comun divisore

1. Trova il massimo comun divisore di ogni denominatore. Scopri se esiste un massimo comune divisore per entrambi i denominatori scoprendo quali numeri sono divisibili per i denominatori.
- Esempio: 3/8 + 5/12
- Fattori di 8: 1, 2, 4, 8
- Fattori di 12: 1, 2, 3, 4, 6, 12

2. Identificare il massimo comune divisore tra i due denominatori. Cerchia tutti i GCD dopo aver trovato i fattori di ciascun denominatore. Il più grande dei GCD è il massimo comune denominatore che puoi utilizzare per risolvere ulteriormente il problema.

3. Moltiplica i denominatori insieme. Vai al passaggio successivo moltiplicando i due denominatori insieme.

4. Condividi dal GCD. Dopo aver trovato il prodotto di entrambi i denominatori, dividilo per il gcd trovato in precedenza. Il risultato di questa divisione è il tuo multiplo minimo comune.

5. Riscrivi il problema originale. Riscrivi i numeratori moltiplicandoli per lo stesso numero impiegato per rendere i corrispondenti denominatori uguali a lcg. Trova il fattore per ciascuna frazione dividendo lcm per il denominatore originale.

6. Risolvere il problema. Con il kgv trovato ora dovrebbe essere possibile aggiungere e sottrarre senza problemi.
Metodo 3 di 4: Fattorizzazione delle frazioni in fattori primi

1. Dividi i denominatori in numeri primi. Dividi ogni denominatore in una serie di numeri primi. Ricorda che i numeri primi sono quei numeri che non possono essere divisi per nessun altro numero tranne 1 e se stesso.
- Esempio: 1/4 + 1/5 + 1/12
- I fattori primi di 4: 2*2
- I fattori primi di 5: 5
- I fattori primi di 12: 2*2*3

2. Conta il numero di volte in cui ogni numero primo si verifica nell`insieme dei fattori primi. Turf il numero di volte in cui ogni numero primo ricorre nei fattori primi di ogni denominatore.

3. Prendi il numero più grande per qualsiasi numero primo. Nota quante volte hai usato ciascun numero primo.

4. Scrivi questo come esempio di seguito.

5. Moltiplica tutti i numeri primi in questo modo. Moltiplica i numeri primi della serie precedente. Il prodotto di questi numeri è uguale a lcm del problema originale.

6. Riscrivi il problema originale. Dividere l`LCF per il denominatore originale. Moltiplica ogni numeratore per lo stesso numero necessario per rendere il denominatore corrispondente l`LCF.

7. Risolvere. Con la LCF trovata e i denominatori simili è diventato facile aggiungere e sottrarre le frazioni come al solito.
Metodo 4 di 4: Lavorare con numeri interi e misti

1. Converti qualsiasi numero intero e misto in una frazione impropria. Converti numeri misti in frazioni improprie moltiplicando l`intero prima della frazione per il denominatore e aggiungendo il numeratore al prodotto. Converti un intero in una frazione impropria inserendolo come numeratore in una frazione con denominatore `1`.
- Esempio: 8 + 2 1/4 + 2/3
- 8=8/1
- 2 1/4; 2*4 + 1=8 + 1=9; 4/9
- Compito riscritto: 8/1 + 9/4 + 2/3

2. Trova il minimo comune multiplo dei denominatori. Applicare uno dei metodi per trovare l`LCF di una frazione comune, come descritto sopra. Si noti che in questo esempio stiamo usando il metodo `Listare i multipli`, creando un elenco di multipli per ogni denominatore e ricavando lcm da questo.

3. Riscrivi il problema originale. Invece di moltiplicare solo il denominatore è necessario moltiplicare anche il numeratore per il numero necessario per rendere il denominatore un lcg.

4. Risolvere il problema. Dopo aver regolato la frazione e trovato lcm al denominatore, dovrebbe essere facile sommare e sottrarre le frazioni senza problemi.
Necessità
- Matita
- Carta
- Calcolatrice (opzionale)
Articoli sull'argomento "Trova il minimo comune multiplo di due denominatori"
Condividi sui social network:
Popolare